Priekšnosacījums: Lineārā regresija

Lineārā regresija ir mašīnmācīšanās algoritms, kura pamatā ir uzraudzīta mācīšanās. Tas veic regresijas uzdevumu. Regresija modelē mērķa prognozēšanas vērtību, pamatojoties uz neatkarīgiem mainīgajiem. To galvenokārt izmanto, lai noskaidrotu saistību starp mainīgajiem lielumiem un prognozēšanu. Dažādi regresijas modeļi atšķiras atkarībā no tā, kāda veida attiecības starp atkarīgo un neatkarīgo mainīgo lielumu tiek ņemtas vērā, kā arī atkarībā no izmantoto neatkarīgo mainīgo skaita. Šajā rakstā tiks parādīts, kā izmantot dažādas Python bibliotēkas, lai ieviestu lineāro regresiju noteiktā datu kopā. Mēs demonstrēsim bināro lineāro modeli, jo to būs vieglāk vizualizēt. Šajā demonstrācijā modelis izmantos Gradient Descent, lai mācītos. Par to varat uzzināt šeit.

1. darbība: Importē visas nepieciešamās bibliotēkas

Python3

import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn> import> preprocessing, svm> from> sklearn.model_selection> import> train_test_split> from> sklearn.linear_model> import> LinearRegression>

2. darbība: Datu kopas lasīšana:

Python3

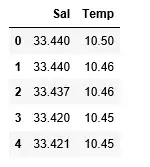
df> => pd.read_csv(> 'bottle.csv'> )> df_binary> => df[[> 'Salnty'> ,> 'T_degC'> ]]> > # Taking only the selected two attributes from the dataset> df_binary.columns> => [> 'Sal'> ,> 'Temp'> ]> #display the first 5 rows> df_binary.head()>

Izvade:

3. darbība: Datu izkliedes izpēte

Python3

#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary, order> => 2> , ci> => None> )> plt.show()>

Izvade:

4. darbība: Datu tīrīšana

Python3

# Eliminating NaN or missing input numbers> df_binary.fillna(method> => 'ffill'> , inplace> => True> )>

5. darbība: Mūsu modeļa apmācība

Python3

X> => np.array(df_binary[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace> => True> )> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > # Splitting the data into training and testing data> regr> => LinearRegression()> > regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Izvade:

6. darbība: Mūsu rezultātu izpēte

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()> # Data scatter of predicted values>

Izvade:

Mūsu modeļa zemais precizitātes rādītājs liecina, ka mūsu regresīvais modelis nav ļoti labi saderīgs ar esošajiem datiem. Tas liecina, ka mūsu dati nav piemēroti lineārai regresijai. Bet dažreiz datu kopa var pieņemt lineāro regresoru, ja ņemam vērā tikai daļu no tā. Ļaujiet mums pārbaudīt šo iespēju.

7. darbība: Darbs ar mazāku datu kopu

Python3

df_binary500> => df_binary[:][:> 500> ]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x> => 'Sal'> , y> => 'Temp'> , data> => df_binary500,> > order> => 2> , ci> => None> )>

Izvade:

Mēs jau redzam, ka pirmās 500 rindas seko lineāram modelim. Turpiniet ar tām pašām darbībām kā iepriekš.

Python3

df_binary500.fillna(method> => 'fill'> , inplace> => True> )> > X> => np.array(df_binary500[> 'Sal'> ]).reshape(> -> 1> ,> 1> )> y> => np.array(df_binary500[> 'Temp'> ]).reshape(> -> 1> ,> 1> )> > df_binary500.dropna(inplace> => True> )> X_train, X_test, y_train, y_test> => train_test_split(X, y, test_size> => 0.25> )> > regr> => LinearRegression()> regr.fit(X_train, y_train)> print> (regr.score(X_test, y_test))>

Izvade:

Python3

y_pred> => regr.predict(X_test)> plt.scatter(X_test, y_test, color> => 'b'> )> plt.plot(X_test, y_pred, color> => 'k'> )> > plt.show()>

Izvade:

8. darbība: Regresijas novērtēšanas metrika

Visbeidzot, mēs pārbaudām Lineārās regresijas modeļa veiktspēju ar novērtēšanas metrikas palīdzību. Regresijas algoritmiem mēs plaši izmantojam vidējo_absolūto_kļūdu un vidējo_kvadrātu_error metriku, lai pārbaudītu modeļa veiktspēju.

Python3

from> sklearn.metrics> import> mean_absolute_error,mean_squared_error> > mae> => mean_absolute_error(y_true> => y_test,y_pred> => y_pred)> #squared True returns MSE value, False returns RMSE value.> mse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred)> #default=True> rmse> => mean_squared_error(y_true> => y_test,y_pred> => y_pred,squared> => False> )> > print> (> 'MAE:'> ,mae)> print> (> 'MSE:'> ,mse)> print> (> 'RMSE:'> ,rmse)>

Izvade:

MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078