Datu struktūras ir veids, kā sakārtot datus tā, lai tiem varētu piekļūt efektīvāk atkarībā no situācijas. Datu struktūras ir jebkuras programmēšanas valodas pamati, ap kuru tiek veidota programma. Python palīdz apgūt šo datu struktūru pamatus vienkāršāk, salīdzinot ar citām programmēšanas valodām.

Šajā rakstā mēs apspriedīsim datu struktūras Python programmēšanas valodā un to, kā tās ir saistītas ar dažām īpašām iebūvētām datu struktūrām, piemēram, sarakstu kopas, vārdnīcas utt., kā arī dažas uzlabotas datu struktūras, piemēram, koki, grafiki utt.

Saraksti

Python saraksti ir tāpat kā masīvi, kas deklarēti citās valodās, kas ir sakārtota datu kolekcija. Tas ir ļoti elastīgs, jo saraksta vienumiem nav jābūt viena veida.

Python List ieviešana ir līdzīga Vectors C++ vai ArrayList Java. Dārgā darbība ir elementa ievietošana vai dzēšana no saraksta sākuma, jo visi elementi ir jāpārvieto. Ievietošana un dzēšana saraksta beigās var kļūt dārga arī gadījumā, ja iepriekš piešķirtā atmiņa kļūst pilna.

Mēs varam izveidot sarakstu python, kā parādīts zemāk.

Piemērs: Python saraksta izveide

Python3

List> => [> 1> ,> 2> ,> 3> ,> 'GFG'> ,> 2.3> ]> print> (> List> )>

Izvade

[1, 2, 3, 'GFG', 2.3] 

Saraksta elementiem var piekļūt, izmantojot piešķirto indeksu. Saraksta python sākuma indeksā secība ir 0 un beigu indekss (ja ir N elementi) N-1.

Piemērs: Python saraksta darbības

Python3

# Creating a List with> # the use of multiple values> List> => [> 'Geeks'> ,> 'For'> ,> 'Geeks'> ]> print> (> ' List containing multiple values: '> )> print> (> List> )> # Creating a Multi-Dimensional List> # (By Nesting a list inside a List)> List2> => [[> 'Geeks'> ,> 'For'> ], [> 'Geeks'> ]]> print> (> ' Multi-Dimensional List: '> )> print> (List2)> # accessing a element from the> # list using index number> print> (> 'Accessing element from the list'> )> print> (> List> [> 0> ])> print> (> List> [> 2> ])> # accessing a element using> # negative indexing> print> (> 'Accessing element using negative indexing'> )> > # print the last element of list> print> (> List> [> -> 1> ])> > # print the third last element of list> print> (> List> [> -> 3> ])>

Izvade

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Vārdnīca

Python vārdnīca ir kā hash tabulas jebkurā citā valodā ar laika sarežģītību O(1). Tā ir nesakārtota datu vērtību kolekcija, ko izmanto, lai saglabātu datu vērtības, piemēram, karti, kurā atšķirībā no citiem datu tipiem, kuru elements satur tikai vienu vērtību, vārdnīcā ir atslēgas:vērtības pāris. Atslēgas vērtība ir norādīta vārdnīcā, lai padarītu to optimizētāku.

Python vārdnīcas indeksācija tiek veikta ar taustiņu palīdzību. Tie ir jebkura veida jaukšanas veidi, t.i., objekti, kas nekad nevar mainīties, piemēram, virknes, skaitļi, korteži utt. Mēs varam izveidot vārdnīcu, izmantojot krokainas figūriekavas ({}) vai vārdnīcas izpratne .

Piemērs: Python vārdnīcas darbības

Python3

# Creating a Dictionary> Dict> => {> 'Name'> :> 'Geeks'> ,> 1> : [> 1> ,> 2> ,> 3> ,> 4> ]}> print> (> 'Creating Dictionary: '> )> print> (> Dict> )> # accessing a element using key> print> (> 'Accessing a element using key:'> )> print> (> Dict> [> 'Name'> ])> # accessing a element using get()> # method> print> (> 'Accessing a element using get:'> )> print> (> Dict> .get(> 1> ))> # creation using Dictionary comprehension> myDict> => {x: x> *> *> 2> for> x> in> [> 1> ,> 2> ,> 3> ,> 4> ,> 5> ]}> print> (myDict)>

Izvade

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Tuple

Python Tuple ir Python objektu kolekcija, kas līdzinās sarakstam, taču Korpusi pēc būtības ir nemainīgi, t.i., kortejā esošos elementus nevar pievienot vai noņemt pēc izveides. Tāpat kā sarakstā, arī Tuple var saturēt dažāda veida elementus.

Programmā Python korteži tiek izveidoti, ievietojot vērtību secību, kas atdalīta ar “komatu”, izmantojot vai neizmantojot iekavas datu secības grupēšanai.

Piezīme: Korpusus var izveidot arī ar vienu elementu, taču tas ir nedaudz sarežģīti. Nepietiek ar vienu elementu iekavās; beigās ir jābūt “komatam”, lai padarītu to par virkni.

Piemērs: Python Tuple Operations

Python3

# Creating a Tuple with> # the use of Strings> Tuple> => (> 'Geeks'> ,> 'For'> )> print> (> ' Tuple with the use of String: '> )> print> (> Tuple> )> > # Creating a Tuple with> # the use of list> list1> => [> 1> ,> 2> ,> 4> ,> 5> ,> 6> ]> print> (> ' Tuple using List: '> )> Tuple> => tuple> (list1)> # Accessing element using indexing> print> (> 'First element of tuple'> )> print> (> Tuple> [> 0> ])> # Accessing element from last> # negative indexing> print> (> ' Last element of tuple'> )> print> (> Tuple> [> -> 1> ])> > print> (> ' Third last element of tuple'> )> print> (> Tuple> [> -> 3> ])>

Izvade

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Iestatīt

Python komplekts ir nesakārtota datu kolekcija, kas ir mainīga un nepieļauj elementu dublikātus. Kopas pamatā tiek izmantotas, lai iekļautu dalības testēšanu un dublēto ierakstu novēršanu. Šajā procesā izmantotā datu struktūra ir jaukšana — populārs paņēmiens, lai vidēji O(1) veiktu ievietošanu, dzēšanu un šķērsošanu.

Ja vienā indeksa pozīcijā ir vairākas vērtības, vērtība tiek pievienota šai indeksa pozīcijai, lai izveidotu saistīto sarakstu. CPython komplekti tiek ieviesti, izmantojot vārdnīcu ar fiktīviem mainīgajiem, kur galvenās būtnes dalībnieki iestata ar lielāku laika sarežģītības optimizāciju.

Iestatījuma ieviešana:

Komplekti ar daudzām darbībām vienā HashTable:

Piemērs: Python Set Operations

Python3

# Creating a Set with> # a mixed type of values> # (Having numbers and strings)> Set> => set> ([> 1> ,> 2> ,> 'Geeks'> ,> 4> ,> 'For'> ,> 6> ,> 'Geeks'> ])> print> (> ' Set with the use of Mixed Values'> )> print> (> Set> )> # Accessing element using> # for loop> print> (> ' Elements of set: '> )> for> i> in> Set> :> > print> (i, end> => ' '> )> print> ()> # Checking the element> # using in keyword> print> (> 'Geeks'> in> Set> )>

Izvade

Set with the use of Mixed Values {1, 2, 'Geeks', 4, 6, 'For'} Elements of set: 1 2 Geeks 4 6 For True 

Saldēti komplekti

Iesaldētās kopas Python ir nemainīgi objekti, kas atbalsta tikai metodes un operatorus, kas rada rezultātu, neietekmējot iesaldēto kopu vai kopas, kurām tās tiek lietotas. Lai gan kopas elementus var mainīt jebkurā laikā, iesaldētās kopas elementi pēc izveides paliek nemainīgi.

Ja parametri netiek nodoti, tas atgriež tukšu iesaldēto kopu.

Python3

# Same as {'a', 'b','c'}> normal_set> => set> ([> 'a'> ,> 'b'> ,> 'c'> ])> print> (> 'Normal Set'> )> print> (normal_set)> # A frozen set> frozen_set> => frozenset> ([> 'e'> ,> 'f'> ,> 'g'> ])> print> (> ' Frozen Set'> )> print> (frozen_set)> # Uncommenting below line would cause error as> # we are trying to add element to a frozen set> # frozen_set.add('h')>

Izvade

Normal Set {'a', 'c', 'b'} Frozen Set frozenset({'g', 'e', 'f'}) 

Stīga

Python virknes ir baitu masīvi, kas attēlo unikoda rakstzīmes. Vienkāršāk sakot, virkne ir nemainīgs rakstzīmju masīvs. Python nav rakstzīmju datu tipa, viena rakstzīme ir vienkārši virkne, kuras garums ir 1.

Piezīme: Tā kā virknes ir nemainīgas, virknes modificēšanas rezultātā tiks izveidota jauna kopija.

Piemērs: Python stīgu darbības

Python3

String> => 'Welcome to GeeksForGeeks'> print> (> 'Creating String: '> )> print> (String)> > # Printing First character> print> (> ' First character of String is: '> )> print> (String[> 0> ])> > # Printing Last character> print> (> ' Last character of String is: '> )> print> (String[> -> 1> ])>

Izvade

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Bytearray

Python Bytearray sniedz mainīgu veselu skaitļu secību diapazonā 0 <= x < 256.

Piemērs: Python Bytearray operācijas

Python3

# Creating bytearray> a> => bytearray((> 12> ,> 8> ,> 25> ,> 2> ))> print> (> 'Creating Bytearray:'> )> print> (a)> # accessing elements> print> (> ' Accessing Elements:'> , a[> 1> ])> # modifying elements> a[> 1> ]> => 3> print> (> ' After Modifying:'> )> print> (a)> # Appending elements> a.append(> 30> )> print> (> ' After Adding Elements:'> )> print> (a)>

Izvade

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Līdz šim mēs esam pētījuši visas datu struktūras, kas ir iebūvētas Python galvenajā sistēmā. Tagad iedziļinieties Python un skatiet kolekciju moduli, kas nodrošina dažus konteinerus, kas ir noderīgi daudzos gadījumos un nodrošina vairāk funkciju nekā iepriekš definētās funkcijas.

Kolekciju modulis

Python kolekcijas modulis tika ieviests, lai uzlabotu iebūvēto datu tipu funkcionalitāti. Tas nodrošina dažādus konteinerus, apskatīsim katru no tiem sīkāk.

Skaitītāji

Skaitītājs ir vārdnīcas apakšklase. To izmanto, lai saglabātu iterējamā elementu skaitu nesakārtotas vārdnīcas veidā, kur atslēga apzīmē elementu iterējamā un vērtība apzīmē šī elementa skaitu iterējamā. Tas ir līdzvērtīgs citu valodu kopumam vai vairākām valodām.

Piemērs: Python skaitītāja darbības

Python3

from> collections> import> Counter> > # With sequence of items> print> (Counter([> 'B'> ,> 'B'> ,> 'A'> ,> 'B'> ,> 'C'> ,> 'A'> ,> 'B'> ,> 'B'> ,> 'A'> ,> 'C'> ]))> > # with dictionary> count> => Counter({> 'A'> :> 3> ,> 'B'> :> 5> ,> 'C'> :> 2> })> print> (count)> count.update([> 'A'> ,> 1> ])> print> (count)>

Izvade

Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 3, 'C': 2}) Counter({'B': 5, 'A': 4, 'C': 2, 1: 1}) 

PasūtītsDikts

An PasūtītsDikts ir arī vārdnīcas apakšklase, taču atšķirībā no vārdnīcas tā atceras secību, kādā tika ievietoti taustiņi.

Piemērs: Python OrderedDict operācijas

Python3

from> collections> import> OrderedDict> print> (> 'Before deleting: '> )> od> => OrderedDict()> od[> 'a'> ]> => 1> od[> 'b'> ]> => 2> od[> 'c'> ]> => 3> od[> 'd'> ]> => 4> for> key, value> in> od.items():> > print> (key, value)> print> (> ' After deleting: '> )> od.pop(> 'c'> )> for> key, value> in> od.items():> > print> (key, value)> print> (> ' After re-inserting: '> )> od[> 'c'> ]> => 3> for> key, value> in> od.items():> > print> (key, value)>

Izvade

Before deleting: a 1 b 2 c 3 d 4 After deleting: a 1 b 2 d 4 After re-inserting: a 1 b 2 d 4 c 3 

DefaultDict

DefaultDict tiek izmantots, lai nodrošinātu dažas noklusējuma vērtības atslēgai, kas neeksistē un nekad neizraisa KeyError. Tās objektus var inicializēt, izmantojot DefaultDict() metodi, nododot datu tipu kā argumentu.

Piezīme: default_factory ir funkcija, kas nodrošina izveidotās vārdnīcas noklusējuma vērtību. Ja šī parametra nav, tiek parādīts KeyError.

Piemērs: Python DefaultDict operācijas

Python3

from> collections> import> defaultdict> > # Defining the dict> d> => defaultdict(> int> )> > L> => [> 1> ,> 2> ,> 3> ,> 4> ,> 2> ,> 4> ,> 1> ,> 2> ]> > # Iterate through the list> # for keeping the count> for> i> in> L:> > > # The default value is 0> > # so there is no need to> > # enter the key first> > d[i]> +> => 1> > print> (d)>

Izvade

defaultdict(, {1: 2, 2: 3, 3: 1, 4: 2}) 

Ķēdes karte

ChainMap iekapsulē daudzas vārdnīcas vienā vienībā un atgriež vārdnīcu sarakstu. Ja ir jāatrod atslēga, tad visas vārdnīcas tiek meklētas pa vienai, līdz tiek atrasta atslēga.

Piemērs: Python ChainMap operācijas

Python3

from> collections> import> ChainMap> > > d1> => {> 'a'> :> 1> ,> 'b'> :> 2> }> d2> => {> 'c'> :> 3> ,> 'd'> :> 4> }> d3> => {> 'e'> :> 5> ,> 'f'> :> 6> }> > # Defining the chainmap> c> => ChainMap(d1, d2, d3)> print> (c)> print> (c[> 'a'> ])> print> (c[> 'g'> ])>

Izvade

ChainMap({'a': 1, 'b': 2}, {'c': 3, 'd': 4}, {'e': 5, 'f': 6}) 1 

KeyError: 'g' 

Nosaukts Tuple

A Nosaukts Tuple atgriež korešu objektu ar nosaukumiem katrai pozīcijai, kuras trūkst parastajiem kortežiem. Piemēram, apsveriet studentu nosaukumi, kur pirmais elements apzīmē fname, otrais apzīmē lname un trešais elements apzīmē DOB. Pieņemsim, ka, lai izsauktu fname, nevis atcerētos indeksa pozīciju, jūs faktiski varat izsaukt elementu, izmantojot argumentu fname, tad būs ļoti viegli piekļūt elementam korteži. Šo funkcionalitāti nodrošina NamedTuple.

Piemērs: Python NamedTuple operācijas

Python3

from> collections> import> namedtuple> > # Declaring namedtuple()> Student> => namedtuple(> 'Student'> ,[> 'name'> ,> 'age'> ,> 'DOB'> ])> > # Adding values> S> => Student(> 'Nandini'> ,> '19'> ,> '2541997'> )> > # Access using index> print> (> 'The Student age using index is : '> ,end> => '')> print> (S[> 1> ])> > # Access using name> print> (> 'The Student name using keyname is : '> ,end> => '')> print> (S.name)>

Izvade

The Student age using index is : 19 The Student name using keyname is : Nandini 

Par ko

Deque (dubultā rinda) ir optimizēts saraksts ātrākām pievienošanas un pop operācijām no abām konteinera pusēm. Tas nodrošina O(1) laika sarežģītību pievienošanas un pop operācijām, salīdzinot ar sarakstu ar O(n) laika sarežģītību.

Python Deque tiek ieviests, izmantojot divkārši saistītus sarakstus, tāpēc veiktspēja nejaušai piekļuvei elementiem ir O(n).

Piemērs: Python Deque operācijas

Python3

# importing 'collections' for deque operations> import> collections> # initializing deque> de> => collections.deque([> 1> ,> 2> ,> 3> ])> # using append() to insert element at right end> # inserts 4 at the end of deque> de.append(> 4> )> # printing modified deque> print> (> 'The deque after appending at right is : '> )> print> (de)> # using appendleft() to insert element at left end> # inserts 6 at the beginning of deque> de.appendleft(> 6> )> # printing modified deque> print> (> 'The deque after appending at left is : '> )> print> (de)> # using pop() to delete element from right end> # deletes 4 from the right end of deque> de.pop()> # printing modified deque> print> (> 'The deque after deleting from right is : '> )> print> (de)> # using popleft() to delete element from left end> # deletes 6 from the left end of deque> de.popleft()> # printing modified deque> print> (> 'The deque after deleting from left is : '> )> print> (de)>

Izvade

The deque after appending at right is : deque([1, 2, 3, 4]) The deque after appending at left is : deque([6, 1, 2, 3, 4]) The deque after deleting from right is : deque([6, 1, 2, 3]) The deque after deleting from left is : deque([1, 2, 3]) 

UserDict

UserDict ir vārdnīcai līdzīgs konteiners, kas darbojas kā iesaiņojums ap vārdnīcas objektiem. Šis konteiners tiek izmantots, ja kāds vēlas izveidot savu vārdnīcu ar kādu modificētu vai jaunu funkcionalitāti.

Piemērs: Python UserDict

Python3

from> collections> import> UserDict> # Creating a Dictionary where> # deletion is not allowed> class> MyDict(UserDict):> > > # Function to stop deletion> > # from dictionary> > def> __del__(> self> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop pop from> > # dictionary> > def> pop(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop popitem> > # from Dictionary> > def> popitem(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > # Driver's code> d> => MyDict({> 'a'> :> 1> ,> > 'b'> :> 2> ,> > 'c'> :> 3> })> print> (> 'Original Dictionary'> )> print> (d)> d.pop(> 1> )>

Izvade

Original Dictionary {'a': 1, 'b': 2, 'c': 3} 

RuntimeError: Deletion not allowed 

Lietotāju saraksts

UserList ir sarakstam līdzīgs konteiners, kas darbojas kā iesaiņojums ap saraksta objektiem. Tas ir noderīgi, ja kāds vēlas izveidot savu sarakstu ar kādu modificētu vai papildu funkcionalitāti.

Piemēri: Python UserList

Python3

# Python program to demonstrate> # userlist> from> collections> import> UserList> # Creating a List where> # deletion is not allowed> class> MyList(UserList):> > > # Function to stop deletion> > # from List> > def> remove(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > > # Function to stop pop from> > # List> > def> pop(> self> , s> => None> ):> > raise> RuntimeError(> 'Deletion not allowed'> )> > # Driver's code> L> => MyList([> 1> ,> 2> ,> 3> ,> 4> ])> print> (> 'Original List'> )> print> (L)> # Inserting to List'> L.append(> 5> )> print> (> 'After Insertion'> )> print> (L)> # Deleting From List> L.remove()>

Izvade

Original List [1, 2, 3, 4] After Insertion [1, 2, 3, 4, 5] 

RuntimeError: Deletion not allowed 

UserString

UserString ir virknei līdzīgs konteiners, un tāpat kā UserDict un UserList tas darbojas kā iesaiņojums ap virknes objektiem. To izmanto, ja kāds vēlas izveidot savas virknes ar kādu modificētu vai papildu funkcionalitāti.

Piemērs: Python UserString

Python3

from> collections> import> UserString> # Creating a Mutable String> class> Mystring(UserString):> > > # Function to append to> > # string> > def> append(> self> , s):> > self> .data> +> => s> > > # Function to remove from> > # string> > def> remove(> self> , s):> > self> .data> => self> .data.replace(s, '')> > # Driver's code> s1> => Mystring(> 'Geeks'> )> print> (> 'Original String:'> , s1.data)> # Appending to string> s1.append(> 's'> )> print> (> 'String After Appending:'> , s1.data)> # Removing from string> s1.remove(> 'e'> )> print> (> 'String after Removing:'> , s1.data)>

Izvade

Original String: Geeks String After Appending: Geekss String after Removing: Gkss 

Tagad, izpētot visas datu struktūras, apskatīsim dažas uzlabotas datu struktūras, piemēram, steku, rindu, grafiku, saistīto sarakstu utt., ko var izmantot Python valodā.

Saistītais saraksts

Saistītais saraksts ir lineāra datu struktūra, kurā elementi netiek glabāti blakus esošās atmiņas vietās. Saistītā saraksta elementi ir saistīti, izmantojot norādes, kā parādīts zemāk esošajā attēlā:

Saistīts saraksts tiek attēlots ar rādītāju uz saistītā saraksta pirmo mezglu. Pirmo mezglu sauc par galvu. Ja saistītais saraksts ir tukšs, galvas vērtība ir NULL. Katrs mezgls sarakstā sastāv no vismaz divām daļām:

• Dati
• Rādītājs (vai atsauce) uz nākamo mezglu

Piemērs: Saistītā saraksta definēšana programmā Python

Python3

# Node class> class> Node:> > # Function to initialize the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize> > # next as null> # Linked List class> class> LinkedList:> > > # Function to initialize the Linked> > # List object> > def> __init__(> self> ):> > self> .head> => None>

Izveidosim vienkāršu saistīto sarakstu ar 3 mezgliem.

Python3

# A simple Python program to introduce a linked list> # Node class> class> Node:> > # Function to initialise the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize next as null> # Linked List class contains a Node object> class> LinkedList:> > # Function to initialize head> > def> __init__(> self> ):> > self> .head> => None> # Code execution starts here> if> __name__> => => '__main__'> :> > # Start with the empty list> > list> => LinkedList()> > list> .head> => Node(> 1> )> > second> => Node(> 2> )> > third> => Node(> 3> )> > '''> > Three nodes have been created.> > We have references to these three blocks as head,> > second and third> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | None | | 2 | None | | 3 | None |> > +----+------+ +----+------+ +----+------+> > '''> > list> .head.> next> => second;> # Link first node with second> > '''> > Now next of first Node refers to second. So they> > both are linked.> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | o-------->| 2 | null | | 3 | null |> > +----+------+ +----+------+ +----+------+> > '''> > second.> next> => third;> # Link second node with the third node> > '''> > Now next of second Node refers to third. So all three> > nodes are linked.> > list.head second third> > | | |> > | | |> > +----+------+ +----+------+ +----+------+> > | 1 | o-------->| 2 | o-------->| 3 | null |> > +----+------+ +----+------+ +----+------+> > '''>

Saistītā saraksta apceļošana

Iepriekšējā programmā mēs esam izveidojuši vienkāršu saistīto sarakstu ar trim mezgliem. Izbrauksim izveidoto sarakstu un izdrukāsim katra mezgla datus. Lai veiktu pārvietošanos, uzrakstīsim vispārējas nozīmes funkciju printList(), kas izdrukā jebkuru sarakstu.

Python3

# A simple Python program for traversal of a linked list> # Node class> class> Node:> > # Function to initialise the node object> > def> __init__(> self> , data):> > self> .data> => data> # Assign data> > self> .> next> => None> # Initialize next as null> # Linked List class contains a Node object> class> LinkedList:> > # Function to initialize head> > def> __init__(> self> ):> > self> .head> => None> > # This function prints contents of linked list> > # starting from head> > def> printList(> self> ):> > temp> => self> .head> > while> (temp):> > print> (temp.data)> > temp> => temp.> next> # Code execution starts here> if> __name__> => => '__main__'> :> > # Start with the empty list> > list> => LinkedList()> > list> .head> => Node(> 1> )> > second> => Node(> 2> )> > third> => Node(> 3> )> > list> .head.> next> => second;> # Link first node with second> > second.> next> => third;> # Link second node with the third node> > list> .printList()>

Izvade

1 2 3 

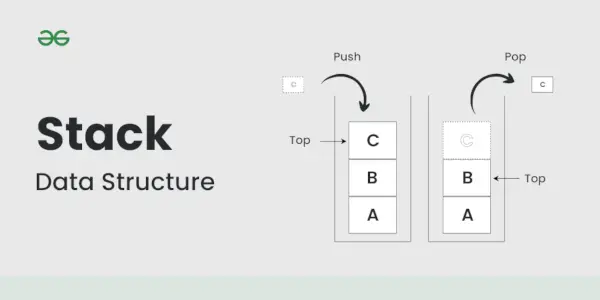
Kaudze

A kaudze ir lineāra datu struktūra, kas saglabā vienumus pēdējā ienākošā/pirmā ārā (LIFO) vai First-In/Last-Out (FILO) veidā. Kaudzē jauns elements tiek pievienots vienā galā un elements tiek noņemts tikai no šī gala. Ievietošanas un dzēšanas darbības bieži sauc par push un pop.

Ar steku saistītās funkcijas ir:

tukšs() – atgriež, vai kaudze ir tukša – laika sarežģītība: O(1) izmērs() – atgriež kaudzes izmēru – laika sarežģītība: O(1) top() – atgriež atsauci uz kaudzes augšējo elementu. – Laika sarežģītība: O(1) push(a) – ievieto elementu “a” kaudzes augšdaļā – Laika sarežģītība: O(1) pop() – dzēš kaudzes augšējo elementu – Laika sarežģītība: O( 1)

Python Stack ieviešana

Stack programmā Python var ieviest, izmantojot šādus veidus:

• sarakstu
• Kolekcijas.deque
• rinda.LifoQueue

Īstenošana, izmantojot sarakstu

Python iebūvēto datu struktūru sarakstu var izmantot kā kaudzi. Push() vietā tiek izmantots append(), lai pievienotu elementus kaudzes augšpusē, savukārt pop() noņem elementu LIFO secībā.

Python3

stack> => []> # append() function to push> # element in the stack> stack.append(> 'g'> )> stack.append(> 'f'> )> stack.append(> 'g'> )> print> (> 'Initial stack'> )> print> (stack)> # pop() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from stack:'> )> print> (stack.pop())> print> (stack.pop())> print> (stack.pop())> print> (> ' Stack after elements are popped:'> )> print> (stack)> # uncommenting print(stack.pop())> # will cause an IndexError> # as the stack is now empty>

Izvade

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Ieviešana, izmantojot collections.deque:

Python steku var ieviest, izmantojot deque klasi no kolekciju moduļa. Deque ir priekšroka salīdzinājumā ar sarakstu gadījumos, kad mums ir nepieciešamas ātrākas pievienošanas un pop operācijas no abiem konteinera galiem, jo ​​deque nodrošina O(1) laika sarežģītību pievienošanas un pop operācijām, salīdzinot ar sarakstu, kas nodrošina O(n) laika sarežģītība.

Python3

from> collections> import> deque> stack> => deque()> # append() function to push> # element in the stack> stack.append(> 'g'> )> stack.append(> 'f'> )> stack.append(> 'g'> )> print> (> 'Initial stack:'> )> print> (stack)> # pop() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from stack:'> )> print> (stack.pop())> print> (stack.pop())> print> (stack.pop())> print> (> ' Stack after elements are popped:'> )> print> (stack)> # uncommenting print(stack.pop())> # will cause an IndexError> # as the stack is now empty>

Izvade

Initial stack: deque(['g', 'f', 'g']) Elements popped from stack: g f g Stack after elements are popped: deque([]) 

Īstenošana, izmantojot rindas moduli

Rindas modulim ir arī LIFO rinda, kas būtībā ir Stack. Dati tiek ievietoti rindā, izmantojot funkciju put() un get() izņem datus no rindas.

Python3

from> queue> import> LifoQueue> # Initializing a stack> stack> => LifoQueue(maxsize> => 3> )> # qsize() show the number of elements> # in the stack> print> (stack.qsize())> # put() function to push> # element in the stack> stack.put(> 'g'> )> stack.put(> 'f'> )> stack.put(> 'g'> )> print> (> 'Full: '> , stack.full())> print> (> 'Size: '> , stack.qsize())> # get() function to pop> # element from stack in> # LIFO order> print> (> ' Elements popped from the stack'> )> print> (stack.get())> print> (stack.get())> print> (stack.get())> print> (> ' Empty: '> , stack.empty())>

Izvade

0 Full: True Size: 3 Elements popped from the stack g f g Empty: True 

Rinda

Kā kaudze, rindā ir lineāra datu struktūra, kas glabā vienumus FIFO (First In First Out) veidā. Ja ir rinda, vispirms tiek noņemts vismazāk pievienotais vienums. Labs rindas piemērs ir jebkura resursa patērētāju rinda, kurā vispirms tiek apkalpots patērētājs, kurš bija pirmais.

Ar rindu saistītās darbības ir:

Rinda: pievieno rindai vienumu. Ja rinda ir pilna, tiek uzskatīts, ka tas ir pārpildes nosacījums — laika sarežģītība: O(1) Rinda: noņem no rindas vienumu. Vienumi tiek izspiesti tādā pašā secībā, kādā tie tiek stumti. Ja rinda ir tukša, tiek uzskatīts, ka tas ir nepietiekamas plūsmas nosacījums — laika sarežģītība: O(1) priekšpuse: iegūstiet priekšējo vienumu no rindas — laika sarežģītība: O(1) aizmugurē: iegūstiet pēdējo vienumu no rindas — laika sarežģītība. : O(1)

Python rindas ieviešana

Python rindu var ieviest šādos veidos:

• sarakstu
• kolekcijas.deque
• aste.aste

Īstenošana, izmantojot sarakstu

enqueue() un dequeue() vietā tiek izmantotas funkcijas append() un pop().

Python3

# Initializing a queue> queue> => []> # Adding elements to the queue> queue.append(> 'g'> )> queue.append(> 'f'> )> queue.append(> 'g'> )> print> (> 'Initial queue'> )> print> (queue)> # Removing elements from the queue> print> (> ' Elements dequeued from queue'> )> print> (queue.pop(> 0> ))> print> (queue.pop(> 0> ))> print> (queue.pop(> 0> ))> print> (> ' Queue after removing elements'> )> print> (queue)> # Uncommenting print(queue.pop(0))> # will raise and IndexError> # as the queue is now empty>

Izvade

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Īstenošana, izmantojot collections.deque

Deque ir priekšroka salīdzinājumā ar sarakstu gadījumos, kad mums ir nepieciešamas ātrākas pievienošanas un pop operācijas no abiem konteinera galiem, jo ​​deque nodrošina O(1) laika sarežģītību pievienošanas un pop operācijām, salīdzinot ar sarakstu, kas nodrošina O(n) laika sarežģītība.

Python3

from> collections> import> deque> # Initializing a queue> q> => deque()> # Adding elements to a queue> q.append(> 'g'> )> q.append(> 'f'> )> q.append(> 'g'> )> print> (> 'Initial queue'> )> print> (q)> # Removing elements from a queue> print> (> ' Elements dequeued from the queue'> )> print> (q.popleft())> print> (q.popleft())> print> (q.popleft())> print> (> ' Queue after removing elements'> )> print> (q)> # Uncommenting q.popleft()> # will raise an IndexError> # as queue is now empty>

Izvade

Initial queue deque(['g', 'f', 'g']) Elements dequeued from the queue g f g Queue after removing elements deque([]) 

Īstenošana, izmantojot rindu.Rinda

queue.Queue(maxsize) inicializē mainīgo līdz maksimālajam izmēram maxsize. Ja maksimālais lielums ir nulle “0”, tas nozīmē bezgalīgu rindu. Šī rinda atbilst FIFO likumam.

Python3

from> queue> import> Queue> # Initializing a queue> q> => Queue(maxsize> => 3> )> # qsize() give the maxsize> # of the Queue> print> (q.qsize())> # Adding of element to queue> q.put(> 'g'> )> q.put(> 'f'> )> q.put(> 'g'> )> # Return Boolean for Full> # Queue> print> (> ' Full: '> , q.full())> # Removing element from queue> print> (> ' Elements dequeued from the queue'> )> print> (q.get())> print> (q.get())> print> (q.get())> # Return Boolean for Empty> # Queue> print> (> ' Empty: '> , q.empty())> q.put(> 1> )> print> (> ' Empty: '> , q.empty())> print> (> 'Full: '> , q.full())> # This would result into Infinite> # Loop as the Queue is empty.> # print(q.get())>

Izvade

0 Full: True Elements dequeued from the queue g f g Empty: True Empty: False Full: False 

Prioritātes rinda

Prioritārās rindas ir abstraktas datu struktūras, kur katram rindas datiem/vērtībai ir noteikta prioritāte. Piemēram, aviokompānijās bagāža ar nosaukumu Business vai First Class pienāk agrāk nekā pārējā. Prioritātes rinda ir rindas paplašinājums ar tālāk norādītajiem rekvizītiem.

• Elements ar augstu prioritāti tiek izslēgts no rindas pirms elementa ar zemu prioritāti.
• Ja diviem elementiem ir vienāda prioritāte, tie tiek apkalpoti atbilstoši to secībai rindā.

Python3

# A simple implementation of Priority Queue> # using Queue.> class> PriorityQueue(> object> ):> > def> __init__(> self> ):> > self> .queue> => []> > def> __str__(> self> ):> > return> ' '> .join([> str> (i)> for> i> in> self> .queue])> > # for checking if the queue is empty> > def> isEmpty(> self> ):> > return> len> (> self> .queue)> => => 0> > # for inserting an element in the queue> > def> insert(> self> , data):> > self> .queue.append(data)> > # for popping an element based on Priority> > def> delete(> self> ):> > try> :> > max> => 0> > for> i> in> range> (> len> (> self> .queue)):> > if> self> .queue[i]>>> :> > myQueue> => PriorityQueue()> > myQueue.insert(> 12> )> > myQueue.insert(> 1> )> > myQueue.insert(> 14> )> > myQueue.insert(> 7> )> > print> (myQueue)> > while> not> myQueue.isEmpty():> > print> (myQueue.delete())>

Izvade

12 1 14 7 14 12 7 1 

Kaudzes rinda (vai kaudzes q)

heapq modulis Python nodrošina kaudzes datu struktūru, ko galvenokārt izmanto, lai attēlotu prioritāro rindu. Šīs Python datu struktūras īpašība ir tāda, ka katru reizi tiek parādīts mazākais kaudzes elements (min-heap). Ikreiz, kad elementi tiek stumti vai izspiesti, kaudzes struktūra tiek saglabāta. Elements hep[0] katru reizi atgriež arī mazāko elementu.

Tas atbalsta mazākā elementa ekstrakciju un ievietošanu O(log n) laikos.

Python3

# importing 'heapq' to implement heap queue> import> heapq> # initializing list> li> => [> 5> ,> 7> ,> 9> ,> 1> ,> 3> ]> # using heapify to convert list into heap> heapq.heapify(li)> # printing created heap> print> (> 'The created heap is : '> ,end> => '')> print> (> list> (li))> # using heappush() to push elements into heap> # pushes 4> heapq.heappush(li,> 4> )> # printing modified heap> print> (> 'The modified heap after push is : '> ,end> => '')> print> (> list> (li))> # using heappop() to pop smallest element> print> (> 'The popped and smallest element is : '> ,end> => '')> print> (heapq.heappop(li))>

Izvade

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Binārais koks

Koks ir hierarhiska datu struktūra, kas izskatās šādi:

 tree ---- j  <-- root /  f k /   a h z  <-- leaves 

Koka augšējo mezglu sauc par sakni, savukārt apakšējos mezglus vai mezglus bez bērniem sauc par lapu mezgliem. Mezglus, kas atrodas tieši zem mezgla, sauc par tā bērniem, un mezglus, kas atrodas tieši virs kaut kā, sauc par tā vecākiem.

Binārais koks ir koks, kura elementos var būt gandrīz divi bērni. Tā kā katram binārā koka elementam var būt tikai 2 bērni, mēs tos parasti nosaucam par kreiso un labo bērnu. Binārā koka mezglā ir šādas daļas.

• Dati
• Rādītājs uz kreiso bērnu
• Norādiet uz pareizo bērnu

Piemērs: mezgla klases definēšana

Python3

# A Python class that represents an individual node> # in a Binary Tree> class> Node:> > def> __init__(> self> ,key):> > self> .left> => None> > self> .right> => None> > self> .val> => key>

Tagad izveidosim koku ar 4 mezgliem Python. Pieņemsim, ka koka struktūra izskatās šādi -

 tree ---- 1  <-- root /  2 3 / 4 

Piemērs: datu pievienošana kokam

Python3

# Python program to introduce Binary Tree> # A class that represents an individual node in a> # Binary Tree> class> Node:> > def> __init__(> self> ,key):> > self> .left> => None> > self> .right> => None> > self> .val> => key> # create root> root> => Node(> 1> )> ''' following is the tree after above statement> > 1> > /> > None None'''> root.left> => Node(> 2> );> root.right> => Node(> 3> );> ''' 2 and 3 become left and right children of 1> > 1> > /> > 2 3> > / /> None None None None'''> root.left.left> => Node(> 4> );> '''4 becomes left child of 2> > 1> > /> > 2 3> > / /> 4 None None None> /> None None'''>

Koku šķērsošana

Kokus var šķērsot dažādos veidos. Tālāk ir norādīti parasti izmantotie koku šķērsošanas veidi. Apskatīsim zemāk esošo koku -

 tree ---- 1  <-- root /  2 3 /  4 5 

Pirmās dziļuma šķērsošanas reizes:

• Kārtība (pa kreisi, sakne, pa labi): 4 2 5 1 3
• Iepriekšēja pasūtīšana (sakne, pa kreisi, pa labi): 1 2 4 5 3
• Postorder (pa kreisi, pa labi, sakne): 4 5 2 3 1

Algoritma secība (koks)

• Pārejiet pa kreiso apakškoku, t.i., izsauciet Inorder(kreisais apakškoks)
• Apmeklējiet sakni.
• Pārejiet pa labo apakškoku, t.i., izsauciet Inorder(labais-apakškoks)

Algoritma priekšpasūtīšana (koks)

• Apmeklējiet sakni.
• Pārvietojiet kreiso apakškoku, t.i., izsauciet Preorder(left-subtree)
• Pārejiet pa labo apakškoku, t.i., izsauciet Preorder(labais-apakškoks)

Algoritms Pasta pasūtījums (koks)

• Pārejiet pa kreiso apakškoku, t.i., izsauciet Postorder(left-subtree)
• Pārejiet pa labo apakškoku, t.i., izsauciet Postorder(labais-apakškoks)
• Apmeklējiet sakni.

Python3

# Python program to for tree traversals> # A class that represents an individual node in a> # Binary Tree> class> Node:> > def> __init__(> self> , key):> > self> .left> => None> > self> .right> => None> > self> .val> => key> # A function to do inorder tree traversal> def> printInorder(root):> > if> root:> > # First recur on left child> > printInorder(root.left)> > # then print the data of node> > print> (root.val),> > # now recur on right child> > printInorder(root.right)> # A function to do postorder tree traversal> def> printPostorder(root):> > if> root:> > # First recur on left child> > printPostorder(root.left)> > # the recur on right child> > printPostorder(root.right)> > # now print the data of node> > print> (root.val),> # A function to do preorder tree traversal> def> printPreorder(root):> > if> root:> > # First print the data of node> > print> (root.val),> > # Then recur on left child> > printPreorder(root.left)> > # Finally recur on right child> > printPreorder(root.right)> # Driver code> root> => Node(> 1> )> root.left> => Node(> 2> )> root.right> => Node(> 3> )> root.left.left> => Node(> 4> )> root.left.right> => Node(> 5> )> print> (> 'Preorder traversal of binary tree is'> )> printPreorder(root)> print> (> ' Inorder traversal of binary tree is'> )> printInorder(root)> print> (> ' Postorder traversal of binary tree is'> )> printPostorder(root)>

Izvade

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Laika sarežģītība — O(n)

Platuma pirmā vai līmeņa pasūtījuma izbraukšana

Līmeņa pasūtījuma šķērsošana koks ir koka šķērsošana platumā. Iepriekš minētā koka līmeņa secības šķērsošana ir 1 2 3 4 5.

Katram mezglam vispirms tiek apmeklēts mezgls un pēc tam tā pakārtotie mezgli tiek ievietoti FIFO rindā. Zemāk ir algoritms tam pašam -

• Izveidojiet tukšu rindu q
• temp_node = sakne /*sākt no saknes*/
• Cilpa, kamēr temp_node nav NULL
  • drukāt temp_node->data.
  • Ievietojiet temp_node bērnu rindas (vispirms kreisās, pēc tam labās puses atvases) uz q
  • Atvienojiet mezglu no q

Python3

# Python program to print level> # order traversal using Queue> # A node structure> class> Node:> > > # A utility function to create a new node> > def> __init__(> self> ,key):> > self> .data> => key> > self> .left> => None> > self> .right> => None> # Iterative Method to print the> # height of a binary tree> def> printLevelOrder(root):> > > # Base Case> > if> root> is> None> :> > return> > > # Create an empty queue> > # for level order traversal> > queue> => []> > # Enqueue Root and initialize height> > queue.append(root)> > while> (> len> (queue)>>> )> printLevelOrder(root)>

Izvade

Level Order Traversal of binary tree is - 1 2 3 4 5 

Laika sarežģītība: O(n)

Grafiks

A grafikā ir nelineāra datu struktūra, kas sastāv no mezgliem un malām. Mezgli dažreiz tiek saukti arī par virsotnēm, un malas ir līnijas vai loki, kas savieno jebkurus divus grafa mezglus. Formālāk grafiku var definēt kā grafiku, kas sastāv no ierobežotas virsotņu (vai mezglu) kopas un malu kopas, kas savieno mezglu pāri.

Iepriekš minētajā grafikā virsotņu kopa V = {0,1,2,3,4} un malu kopa E = {01, 12, 23, 34, 04, 14, 13}.

Tālāk minētie divi ir visbiežāk izmantotie grafika attēlojumi.

• Blakus matrica
• Blakus esošo vietu saraksts

Blakus matrica

Blakusmatrica ir 2D masīvs ar izmēru V x V, kur V ir grafa virsotņu skaits. Lai 2D masīvs ir adj[][], sprauga adj[i][j] = 1 norāda, ka ir mala no virsotnes i līdz virsotnei j. Blakusuma matrica nevirzītam grafikam vienmēr ir simetriska. Blakusuma matricu izmanto arī svērto grafiku attēlošanai. Ja adj[i][j] = w, tad ir mala no virsotnes i līdz virsotnei j ar svaru w.

Python3

# A simple representation of graph using Adjacency Matrix> class> Graph:> > def> __init__(> self> ,numvertex):> > self> .adjMatrix> => [[> -> 1> ]> *> numvertex> for> x> in> range> (numvertex)]> > self> .numvertex> => numvertex> > self> .vertices> => {}> > self> .verticeslist> => [> 0> ]> *> numvertex> > def> set_vertex(> self> ,vtx,> id> ):> > if> 0> <> => vtx <> => self> .numvertex:> > self> .vertices[> id> ]> => vtx> > self> .verticeslist[vtx]> => id> > def> set_edge(> self> ,frm,to,cost> => 0> ):> > frm> => self> .vertices[frm]> > to> => self> .vertices[to]> > self> .adjMatrix[frm][to]> => cost> > > # for directed graph do not add this> > self> .adjMatrix[to][frm]> => cost> > def> get_vertex(> self> ):> > return> self> .verticeslist> > def> get_edges(> self> ):> > edges> => []> > for> i> in> range> (> self> .numvertex):> > for> j> in> range> (> self> .numvertex):> > if> (> self> .adjMatrix[i][j]!> => -> 1> ):> > edges.append((> self> .verticeslist[i],> self> .verticeslist[j],> self> .adjMatrix[i][j]))> > return> edges> > > def> get_matrix(> self> ):> > return> self> .adjMatrix> G> => Graph(> 6> )> G.set_vertex(> 0> ,> 'a'> )> G.set_vertex(> 1> ,> 'b'> )> G.set_vertex(> 2> ,> 'c'> )> G.set_vertex(> 3> ,> 'd'> )> G.set_vertex(> 4> ,> 'e'> )> G.set_vertex(> 5> ,> 'f'> )> G.set_edge(> 'a'> ,> 'e'> ,> 10> )> G.set_edge(> 'a'> ,> 'c'> ,> 20> )> G.set_edge(> 'c'> ,> 'b'> ,> 30> )> G.set_edge(> 'b'> ,> 'e'> ,> 40> )> G.set_edge(> 'e'> ,> 'd'> ,> 50> )> G.set_edge(> 'f'> ,> 'e'> ,> 60> )> print> (> 'Vertices of Graph'> )> print> (G.get_vertex())> print> (> 'Edges of Graph'> )> print> (G.get_edges())> print> (> 'Adjacency Matrix of Graph'> )> print> (G.get_matrix())>

Izvade

Grafika virsotnes

[“a”, “b”, “c”, “d”, “e”, “f”]

Grafika malas

[('a', 'c', 20), ('a', 'e', ​​10), ('b', 'c', 30), ('b', 'e', 40), ( 'c', 'a', 20), ('c', 'b', 30), ('d', 'e', ​​50), ('e', 'a', 10), ('e' ', 'b', 40), ('e', 'd', 50), ('e', 'f', 60), ('f', 'e', ​​60)]

Grafika blakus matrica

[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]

Blakus esošo vietu saraksts

Tiek izmantots sarakstu masīvs. Masīva lielums ir vienāds ar virsotņu skaitu. Ļaujiet masīvam būt masīvam[]. Ieraksta masīvs [i] attēlo virsotņu sarakstu, kas atrodas blakus i-tajai virsotnei. Šo attēlojumu var izmantot arī svērta grafika attēlošanai. Malu svarus var attēlot kā pāru sarakstus. Tālāk ir parādīts iepriekš minētās diagrammas blakus esošo sarakstu attēlojums.

Python3

# A class to represent the adjacency list of the node> class> AdjNode:> > def> __init__(> self> , data):> > self> .vertex> => data> > self> .> next> => None> # A class to represent a graph. A graph> # is the list of the adjacency lists.> # Size of the array will be the no. of the> # vertices 'V'> class> Graph:> > def> __init__(> self> , vertices):> > self> .V> => vertices> > self> .graph> => [> None> ]> *> self> .V> > # Function to add an edge in an undirected graph> > def> add_edge(> self> , src, dest):> > > # Adding the node to the source node> > node> => AdjNode(dest)> > node.> next> => self> .graph[src]> > self> .graph[src]> => node> > # Adding the source node to the destination as> > # it is the undirected graph> > node> => AdjNode(src)> > node.> next> => self> .graph[dest]> > self> .graph[dest]> => node> > # Function to print the graph> > def> print_graph(> self> ):> > for> i> in> range> (> self> .V):> > print> (> 'Adjacency list of vertex {} head'> .> format> (i), end> => '')> > temp> => self> .graph[i]> > while> temp:> > print> (> ' ->{}'> .> format> (temp.vertex), end> => '')> > temp> => temp.> next> > print> (> ' '> )> # Driver program to the above graph class> if> __name__> => => '__main__'> :> > V> => 5> > graph> => Graph(V)> > graph.add_edge(> 0> ,> 1> )> > graph.add_edge(> 0> ,> 4> )> > graph.add_edge(> 1> ,> 2> )> > graph.add_edge(> 1> ,> 3> )> > graph.add_edge(> 1> ,> 4> )> > graph.add_edge(> 2> ,> 3> )> > graph.add_edge(> 3> ,> 4> )> > graph.print_graph()>

Izvade

Adjacency list of vertex 0 head ->4 -> 1 virsotnes blakus esošo saraksts 1 galva -> 4 -> 3 -> 2 -> 0 virsotnes blakus saraksts 2 galva -> 3 -> 1 virsotnes blakus saraksts 3 galva -> 4 -> 2 -> 1 blakus esošais punkts virsotņu saraksts 4 galva -> 3 -> 1 -> 0>>   
Grafika šķērsošana 
  
  Breadth-First meklēšana vai BFS   
  
  Breadth-First Traversal jo grafiks ir līdzīgs koka platuma šķērsošanai. Vienīgā fiksācija šeit ir tāda, ka atšķirībā no kokiem grafikos var būt cikli, tāpēc mēs varam atkal nonākt pie tā paša mezgla. Lai izvairītos no mezgla apstrādes vairāk nekā vienu reizi, mēs izmantojam Būla apmeklēto masīvu. Vienkāršības labad tiek pieņemts, ka visas virsotnes ir sasniedzamas no sākuma virsotnes. 
  
Piemēram, nākamajā grafikā mēs sākam šķērsošanu no 2. virsotnes. Kad nonākam līdz virsotnei 0, mēs meklējam visas tai blakus esošās virsotnes. 2 ir arī blakus virsotne ar 0. Ja mēs neatzīmēsim apmeklētās virsotnes, tad 2 tiks apstrādāts vēlreiz un tas kļūs par procesu, kas nebeidzas. Sekojošā diagrammas pirmā šķērsošana platumā ir 2, 0, 3, 1. 
  
   
  
Python3 
     
 
  
     
   
  
     
  
     
     
     
  
 
  
  
  
  
  # Python3 Program to print BFS traversal>   # from a given source vertex. BFS(int s)>   # traverses vertices reachable from s.>   from>   collections>  import>   defaultdict>   # This class represents a directed graph>   # using adjacency list representation>   class>   Graph:>   >  # Constructor>   >  def>   __init__(>  self>  ):>   >  # default dictionary to store graph>   >  self>  .graph>  =>   defaultdict(>  list>  )>   >  # function to add an edge to graph>   >  def>   addEdge(>  self>  ,u,v):>   >  self>  .graph[u].append(v)>   >  # Function to print a BFS of graph>   >  def>   BFS(>  self>  , s):>   >  # Mark all the vertices as not visited>   >  visited>  =>   [>  False>  ]>  *>   (>  max>  (>  self>  .graph)>  +>   1>  )>   >  # Create a queue for BFS>   >  queue>  =>   []>   >  # Mark the source node as>   >  # visited and enqueue it>   >  queue.append(s)>   >  visited[s]>  =>   True>   >  while>   queue:>   >  # Dequeue a vertex from>   >  # queue and print it>   >  s>  =>   queue.pop(>  0>  )>   >  print>   (s, end>  =>   ' '>  )>   >  # Get all adjacent vertices of the>   >  # dequeued vertex s. If a adjacent>   >  # has not been visited, then mark it>   >  # visited and enqueue it>   >  for>   i>  in>   self>  .graph[s]:>   >  if>   visited[i]>  =>  =>   False>  :>   >  queue.append(i)>   >  visited[i]>  =>   True>   # Driver code>   # Create a graph given in>   # the above diagram>   g>  =>   Graph()>   g.addEdge(>  0>  ,>  1>  )>   g.addEdge(>  0>  ,>  2>  )>   g.addEdge(>  1>  ,>  2>  )>   g.addEdge(>  2>  ,>  0>  )>   g.addEdge(>  2>  ,>  3>  )>   g.addEdge(>  3>  ,>  3>  )>   print>   (>  'Following is Breadth First Traversal'>   >  ' (starting from vertex 2)'>  )>   g.BFS(>  2>  )>   # This code is contributed by Neelam Yadav>   
  
  
  
  
 
     
 
     
 
   
 
  Izvade   
 
  
Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1 
  
Laika sarežģītība: O(V+E), kur V ir grafa virsotņu skaits un E ir grafa malu skaits. 
  
  Pirmā dziļuma meklēšana vai DFS   
  
  Pirmā dziļuma šķērsošana jo grafiks ir līdzīgs koka pirmajam dziļumam. Vienīgā fiksācija šeit ir tāda, ka atšķirībā no kokiem grafikos var būt cikli, mezglu var apmeklēt divas reizes. Lai izvairītos no mezgla apstrādes vairāk nekā vienu reizi, izmantojiet Būla apmeklēto masīvu. 
  
  Algoritms:   
  
  
Izveidojiet rekursīvu funkciju, kas ņem mezgla indeksu un apmeklēto masīvu. 
  
Atzīmējiet pašreizējo mezglu kā apmeklētu un izdrukājiet mezglu. 
  
Pārvietojiet visus blakus esošos un neatzīmētos mezglus un izsauciet rekursīvo funkciju ar blakus esošā mezgla indeksu. 
  
  
Python3 
     
 
  
     
   
  
     
  
     
     
     
  
 
  
  
  
  
  # Python3 program to print DFS traversal>   # from a given graph>   from>   collections>  import>   defaultdict>   # This class represents a directed graph using>   # adjacency list representation>   class>   Graph:>   >  # Constructor>   >  def>   __init__(>  self>  ):>   >  # default dictionary to store graph>   >  self>  .graph>  =>   defaultdict(>  list>  )>   >  # function to add an edge to graph>   >  def>   addEdge(>  self>  , u, v):>   >  self>  .graph[u].append(v)>   >  # A function used by DFS>   >  def>   DFSUtil(>  self>  , v, visited):>   >  # Mark the current node as visited>   >  # and print it>   >  visited.add(v)>   >  print>  (v, end>  =>  ' '>  )>   >  # Recur for all the vertices>   >  # adjacent to this vertex>   >  for>   neighbour>  in>   self>  .graph[v]:>   >  if>   neighbour>  not>   in>   visited:>   >  self>  .DFSUtil(neighbour, visited)>   >  # The function to do DFS traversal. It uses>   >  # recursive DFSUtil()>   >  def>   DFS(>  self>  , v):>   >  # Create a set to store visited vertices>   >  visited>  =>   set>  ()>   >  # Call the recursive helper function>   >  # to print DFS traversal>   >  self>  .DFSUtil(v, visited)>   # Driver code>   # Create a graph given>   # in the above diagram>   g>  =>   Graph()>   g.addEdge(>  0>  ,>  1>  )>   g.addEdge(>  0>  ,>  2>  )>   g.addEdge(>  1>  ,>  2>  )>   g.addEdge(>  2>  ,>  0>  )>   g.addEdge(>  2>  ,>  3>  )>   g.addEdge(>  3>  ,>  3>  )>   print>  (>  'Following is DFS from (starting from vertex 2)'>  )>   g.DFS(>  2>  )>   
  
  
  
  
 
     
 
   
 
     
 
   
 
  Izvade   
 
  
Following is DFS from (starting from vertex 2) 2 0 1 3 
  
Laika sarežģītība: O(V + E), kur V ir virsotņu skaits un E ir grafa malu skaits.