Inerces moments ir ķermeņa īpašība rotācijas kustībā. Inerces moments ir rotējošo ķermeņu īpašība, kas tiecas pretoties ķermeņa rotācijas kustības izmaiņām. Tas ir līdzīgs jebkura ķermeņa inercei translācijas kustībā. Matemātiski inerces moments ir norādīts kā katras daļiņas masas un attāluma no rotācijas ass kvadrāta reizinājuma summa. To mēra vienībās kgm ² .

Tālāk esošajā rakstā sīkāk uzzināsim par inerces momentu.

Satura rādītājs

• Inerces momenta definīcija
• Inerces momenta formula
• Faktori, kas ietekmē inerces momentu
• Kā aprēķināt inerces momentu?
• Inerces momenta formula dažādām formām
• Ģirācijas rādiuss
• Inerces momenta teorēmas
• Inerces mirkļi dažādiem objektiem

Inerces momenta definīcija

Inerces moments ir ķermeņa tendence rotācijas kustībā, kas iebilst pret tā izmaiņām rotācijas kustība ārējo spēku dēļ. Inerces moments darbojas kā leņķiskā masa, un to sauc par rotācijas inerci. Inerces moments ir līdzīgs mehāniskajam Inerce no ķermeņa.

MOI ir definēts kā daudzums, kas izteikts ar reizinājuma summu masu katras daļiņas kvadrāts ar attālumu no rotācijas ass jebkurai daļiņai, kas veic rotācijas kustību.

Inerces momenta mērvienība

Inerces moments ir skalārs lielums, un inerces momenta SI vienība ir kgm ² .

Inerces momenta dimensiju formula

Tā kā inerces moments ir dots kā masas un attāluma kvadrāta reizinājums. Tās izmēru formula tiek iegūts ar masas izmēru formulas un garuma izmēru formulas kvadrāta reizinājumu. Inerces momenta izmēru formula ir: ML ²

Kas ir inerce?

Inerce ir matērijas īpašība, kuras dēļ tai ir tendence pretoties tās kustības stāvokļa izmaiņām. Tas nozīmē, ka ķermenis miera stāvoklī mēģina palikt miera stāvoklī un pretoties jebkuram spēkam, kas mēģina to iekustināt, un kustībā esošais ķermenis mēģina turpināt kustību un pretoties jebkuram spēkam, kas mēģina to panākt, lai mainītu kustības apjomu. Daudzuma ziņā tas ir vienāds ar maksimālo spēku, kas mēģina mainīt tā stāvokli kustība .

Uzziniet vairāk par Inerce .

Inerces momenta formula

Inerces moments ir a skalārais daudzums . Matemātiski daļiņas masas un attāluma no rotācijas ass kvadrāta reizinājumu sauc par daļiņas inerces momentu ap rotācijas asi.

Vispārējā formula jebkura objekta inerces momenta atrašanai ir:

Es = kungs ²

kur,
m ir objekta masa'
r ir attālums no rotācijas ass

Ķermenim, kas sastāv no nepārtrauktām bezgalīgi mazām daļiņām, inerces momenta aprēķināšanai izmanto inerces momenta integrālo formu.

I = ∫dI

es = int_{0}^{M} r^2 dm

Daļiņu sistēmas inerces moments

Daļiņu sistēmas inerces momentu nosaka pēc formulas,

I = ∑m _i r _i ²

kur,
r _i ir perpendikulārais attālums no i ^th daļiņa no ass
m _i ir i masa ^th daļiņa

Iepriekš minētais Inerces momenta vienādojums norāda, ka daļiņu sistēmas inerces moments ir vienāds ar katras daļiņas masas un attāluma kvadrāta no katras daļiņas rotācijas ass reizinājuma summu.

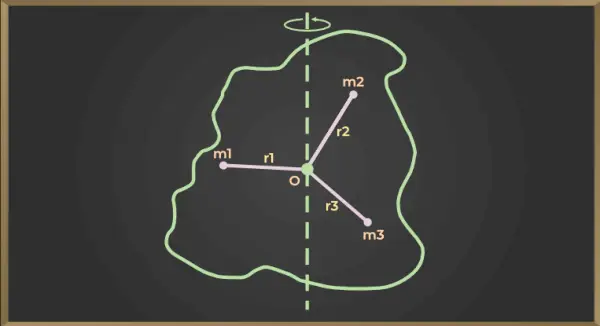
Tālāk norādītajam skaitlim

Pirmās daļiņas inerces moments = m ₁ ×r ₁ ²

Otrās daļiņas inerces moments = m ₂ ×r ₂ ²

Trešās daļiņas inerces moments = m ₃ ×r ₃ ²

Līdzīgi,

Inerces moments n ^th daļiņa = m _n ×r _n ²

Tagad visa ķermeņa inerces moments ap rotācijas asi AB būs vienāds ar visu daļiņu inerces momentu summu, tātad

I = m ₁ ×r ₁ ² + m ₂ ×r ₂ ² + m ₃ ×r ₃ ² +……+m _n ×r _n ²

I = Σm _i ×r _i ²

kur,
es apzīmē ķermeņa inerces momentu ap griešanās asi
m _i ir i masa ^th daļiņa,
r _i ir i rādiuss ^th daļiņa
S atspoguļo summu.

No vienādojuma mēs varam teikt, ka ķermeņa inerces moments ap fiksētu asi ir vienāds ar katras šī ķermeņa daļiņas masas un tās perpendikulārā attāluma no fiksētās ass reizinājuma summu.

Faktori, kas ietekmē inerces momentu

Jebkura objekta inerces moments ir atkarīgs no šādām vērtībām:

• Objekta forma un izmērs
• Objekta materiāla blīvums
• Rotācijas ass

Kā aprēķināt inerces momentu?

Tiek izmantoti vairāki veidi aprēķināt inerces momentu jebkura rotējoša objekta.

• Vienveidīgiem objektiem inerces momentu aprēķina, ņemot to masas reizinājumu ar attāluma no rotācijas ass kvadrātu (r ² ).
• Nevienmērīgiem objektiem mēs aprēķinām inerces momentu, ņemot atsevišķu punktu masu reizinājumu katrā dažādā rādiusā, lai izmantotu formulu:

I = ∑m _i r _i ²

Inerces momenta formula dažādām formām

Šajā tabulā ir aplūkotas dažu simetrisku objektu inerces momenta izteiksmes kopā ar to rotācijas asi:

Objekts	Ass	Inerces momenta izpausme
Dobs cilindrs Plānas sienas	Centrālā	Es = kungs 2
Plāns gredzens	Diametrs	I = 1/2 Mr 2
Gredzenveida gredzens vai dobs cilindrs	Centrālā	I = 1/2 M(r 2 2 + r 1 2 )
Ciets cilindrs	Centrālā	I = 1/2 Mr 2
Vienots disks	Diametrs	I = 1/4 Mr 2
Doba sfēra	Centrālā	I = 2/3 Mr 2
Cieta sfēra	Centrālā	I = 2/5 Mr 2
Vienots simetrisks sfērisks apvalks	Centrālā	I = frac{2}{5}Mfrac{(r_2^5-r_1^5)}{(r_2^3-r_1^3)}
Vienveidīga plāksne vai taisnstūrveida paralēlskaldnis	Centrālā	I = 1/12 M(a 2 + b 2 )
Plāns stienis	Centrālā	I = 1/12 Mr 2
Plāns stienis	Stieņa galā	I = 1/3 Mr 2

Ģirācijas rādiuss

The Ģirācijas rādiuss ķermeņa ir definēts kā perpendikulārs attālums no rotācijas ass līdz masas punktam, kura masa ir vienāda ar visa ķermeņa masu un inerces moments ir vienāds ar objekta faktisko inerces momentu, kāds tas ir bijis. pieņemts, ka tur ir koncentrēta kopējā ķermeņa masa. Tas ir iedomāts attālums. Žirācijas rādiuss ir apzīmēts ar K.

Ja ķermeņa masa un griešanās rādiuss ir attiecīgi M un K, tad ķermeņa inerces moments ir

I = MK ² ……(1)

Tādējādi ķermeņa griešanās rādiuss ir perpendikulārs rotācijas asij, kuras kvadrāts, reizināts ar šī ķermeņa masu, dod ķermeņa inerces momentu ap šo asi.

Atkal ar (1) vienādojumu K ² = I/M

K = √(I/m)

Tādējādi ķermeņa griešanās rādiuss ap asi ir vienāds ar kvadrātsakni no ķermeņa attiecības ap šo asi.

Inerces momenta teorēmas

Ir divu veidu teorēmas, kas ir ļoti svarīgas attiecībā uz inerces momentu:

• Paralēlās ass teorēma
• Perpendikulārās ass teorēma

Perpendikulārās ass teorēma

Perpendikulārās ass teorēma nosaka, ka ķermeņa inerces momenta summa ap divām savstarpēji perpendikulārām asīm, kas atrodas ķermeņa plaknē, ir vienāda ar ķermeņa inerces momentu ap trešo asi, kas ir perpendikulāra abām asīm un iet caur to punktu no krustojuma.

Iepriekš redzamajā attēlā VĒRSIS un LTD ir divas asis ķermeņa plaknē, kas ir perpendikulāras viena otrai. Trešā ass ir OZ kas ir perpendikulāra ķermeņa plaknei un iet caur krustošanās punktu VĒRSIS un LTD cirvji. Ja es _x , es _un , un es _Ar ir ķermeņa inerces momenti ap asi VĒRSIS , LTD , un OZ asis attiecīgi, tad saskaņā ar šo teorēmu

es _x + es _un = es _Ar

Paralēlās ass teorēma

Saskaņā ar Paralēlās ass teorēma , ķermeņa inerces moments ap noteiktu asi ir inerces momenta summa ap asi, kas iet caur šī ķermeņa masas centru, un ķermeņa masas kvadrāta un perpendikulārā attāluma reizinājums starp divas asis.

Ļaujiet parādīties iepriekš minētajā attēlā, mums ir jāatrod inerces moments es _O ķermeņa, kas iet caur punktu O un ap asi, kas ir perpendikulāra plaknei, kamēr ķermeņa inerces moments iet caur masas centru C un ap asi, kas ir paralēla dotajai asij, ir es _C , tad saskaņā ar šo teorēmu

es _O = es _C + ml ²

kur
M ir visa ķermeņa masa
l ir perpendikulārs attālums starp divām asīm.

Inerces mirkļi dažādiem objektiem

Dažādu objektu inerces momenti ir aplūkoti turpmāk šajā rakstā

Taisnstūra plāksnes inerces moments

Ja plāksnes masa ir M, garums l un platums b, tad inerces moments iet caur smaguma centru un ap asi, kas ir perpendikulāra plāksnes plaknei.

I = M(l ² + b ² / 12)

Diska inerces moments

Ja diskam ir masa M un rādiuss r, tad inerces moments ap diska ģeometrisko asi ir

I = 1/2 (Mr ² )

Stieņa inerces moments

Ja stieņa masa ir M un garums ir l, tad inerces moments ap asi, kas ir perpendikulāra stieņa garumam un iet caur tā smaguma centru

I = ML ² /12

Apļa inerces moments

Ja gredzena masa ir M un gredzena rādiuss ir r, tad inerces moments ap asi, kas iet cauri perpendikulāri gredzena centram, ir

Es = kungs ²

Lodes inerces moments

Ja cietas sfēras masa ir M un rādiuss ir r, tad inerces moments ap tās diametru ir

I = 2/5 kungs ²

Cietā cilindra inerces moments

Cieta cilindra ar rādiusu “R” un masu M inerces momentu nosaka ar

I = 1/2MR ²

Doba cilindra inerces moments

Dobajam cilindram ir divi rādiusi, proti, iekšējais rādiuss un ārējais rādiuss. Doba cilindra, kura masa ir M, ārējais rādiuss R, inerces moments ₁ , un iekšējais rādiuss R ₂ tiek dota kā

I = 1/2M(R ₁ ² + R ₂ ² )

Cietas sfēras inerces moments

Masas “M” un rādiusa “R” cietas sfēras inerces moments ir norādīts kā

I = 2/5MR ²

Dobas sfēras inerces moments

Dobas lodes ar masu M un rādiusu “R” inerces moments ir norādīts kā

I = 2/3MR ²

Gredzena inerces moments

Gredzena inerces moments ir dots diviem gadījumiem, kad griešanās ass iet caur centru un kad rotācijas ass iet caur diametru.

Gredzena inerces moments ap asi, kas iet caur centru, ir norādīts ar

I = MR ²

Gredzena inerces moments ap asi, kas iet caur diametru, ir norādīts ar

Es = kungs ² /2

Kvadrāta inerces moments

Malas “a” kvadrāta inerces moments ir dots kā

I = a ⁴ /12

Inerces moments kvadrātveida plāksnei, kuras malas garums ir “l” un masa M, ir norādīts kā

I = 1/6 ml ²

Trijstūra inerces moments

Trijstūra inerces moments ir norādīts 3 situācijās, pirmkārt, kad ass iet caur centru, otrkārt, kad ass iet caur pamatni un treškārt, kad ass ir perpendikulāra pamatnei. Apskatīsim to formulu pa vienam. Trīsstūrim ar pamatni “b” un augstumu “h” inerces momenta formula ir dota šādi

Kad ass iziet cauri centram

I = bh ³ /36

Kad ass iet caur bāzi

I = bh ³ /12

Kad ass ir perpendikulāra pamatnei

I = (hb/36) (b ² – b ₁ b+b ₁ ² )

Atšķirība starp inerces momentu un inerci

Atšķirība starp inerci un inerces momentu ir parādīta tabulā zemāk:

Jā nē.	Inerce	Inerces moments
1.	Tās nozīme ir lineārā kustībā.	Tās nozīme ir rotācijas kustībā.
2.	Tā ir objekta īpašība, kas iebilst pret objekta stāvokļa maiņu lineārā kustībā.	Inerces moments ir objekta īpašība, kas iebilst pret objekta stāvokļa maiņu rotācijas kustībā.
3.	Objekta inerce ir atkarīga tikai no tā masas.	Objekta inerces moments ir atkarīgs no tā masas un masas sadalījuma attiecībā pret rotācijas asi.
4.	Objekta inerce ir fiksēta.	Objekta inerces moments mainās atkarībā no dažādām rotācijas asīm.

Rotējošā ķermeņa kinētiskā enerģija

Pieņemsim, ka ķermenis ar masu “m” griežas ar ātrumu v attālumā “r” no rotācijas ass. Tās leņķiskais ātrums tiek dots ar ω = v/r, tad v = rω. Tagad mēs zinām, ka Kinētiskā enerģija ķermeņa tiek dota ar

KE = 1/2mv ²

⇒ KE = 1/2m(rω) ²

⇒ KE = 1/2mr ² ak ²

⇒ KE = 1/2Iω ²

Tādējādi rotējoša ķermeņa kinētisko enerģiju nosaka puse no inerces momenta un leņķiskais ātrums no ķermeņa. To sauc arī par rotējošā ķermeņa kinētisko enerģiju Rotācijas kinētiskā enerģija . Rotācijas kinētiskās enerģijas formula ir dota kā

KE = 1/2Iω ²

Inerces moments (I) nav atkarīgs no ķermeņa leņķiskā ātruma. Tā ir funkcija no rotējošā ķermeņa masas un ķermeņa attāluma no rotācijas ass. Tādējādi mēs novērojam, ka leņķiskā kustība ir analoga lineārajai kustībai, tas nozīmē, ka inerces momenta nozīme ir tāda, ka tas sniedz priekšstatu par to, kā masas tiek sadalītas dažādos attālumos no rotācijas ass rotējošā ķermenī.

Inerces momenta pielietojums

Inerces momentam ir dažādi pielietojumi, no kuriem daži ir apskatīti tālāk:

• Lielāka inerces momenta dēļ zeme griežas ap savu asi ar tādu pašu leņķisko ātrumu.
• Zem bērnu rotaļu motora ir novietots neliels kustīgs ritenis. Pēc šī riteņa berzēšanas ar zemi un atstāšanas no motora riteņa inerces momenta dēļ motors kādu laiku turpina darboties.
• Katrs dzinējs sastāv no liela un smaga riteņa, kas piestiprināts pie vārpstas, un lielākā daļa tā masas atrodas uz tā apkārtmēra. Tāpēc tā inerces moments ir augsts. Šo riteni sauc par spararatu. Griezes moments, kas virza dzinēja vārpstu, turpina pieaugt. Tāpēc vārpstas rotācija var nebūt vienmērīga, bet kustīga riteņa klātbūtnes dēļ ar lielāku inerci vārpsta turpina griezties ar gandrīz vienmērīgu ātrumu.
• Vēršu pajūgu, rikšu, skrejriteņu, velosipēdu utt. ritenī lielākā masas daļa ir koncentrēta uz tā apļa vai loka. šī stīpa vai rutīna ir piestiprināta pie riteņa ass ar stingriem spieķiem. To darot, palielinās tā inerces moments. Tāpēc, kad riteņbraukšanas laikā kājas pārstāj kustēties, ritenis kādu laiku turpina griezties.

Tāpat pārbaudiet

• Rotācijas kustības kinemātika
• Stingra ķermeņa kustība
• Ritošā kustība

Atrisināti piemēri par inerces momentiem

1. piemērs: ķermenis, kura masa ir 500 g, griežas ap asi. ķermeņa masas centra attālums no rotācijas ass ir 1,2 m. atrast ķermeņa inerces momentu ap griešanās asi.

Risinājums:

Ņemot vērā, ka M = 500 g = 0,5 kg, r = 1,2 m.

Acīmredzot var pieņemt, ka visa ķermeņa masa atrodas tā masas centrā. Tad ķermeņa inerces moments ap griešanās asi.

Es = kungs ²

I = 0,5 × (1,2) ²

I = 0,72 kg m ²

2. piemērs. Apgrieziena rādiuss ap asi, kas atrodas 12 cm attālumā no ķermeņa, kura masa ir 1,2 kg, masas centra ir 13 cm. Aprēķiniet apgriezienu rādiuss un inerces moments ap asi, kas iet caur masas centru.

Risinājums:

Ņemot vērā to, ka M = 1,0 kg, K = 13 cm, l = 12 cm, K _CM =?, es _CM = ?

No paralēlās ass teorēmas I = I _CM + ml ²

K ² = K _CM2 + l ²

vai K _CM2 = K ² – l ²

K _CM2 = (13) ² – (12) ² = 25

K _CM = 5

Tagad Inerces moments I _CM = MK _CM2

es _CM = 1,0 × (0,05) ² = 2,5 × 10 ^-3 kg m ²

3. piemērs: ķermenis, kura masa ir 0,1 kg, griežas ap asi. ja ķermeņa masas centra attālums no rotācijas ass ir 0,5 m, tad atrod ķermeņa inerces momentu.

Risinājums:

Ņemot vērā to, M = 0,1 kg un r = 0,5 m

tātad es = Mr ²

I = 0,1 × (0,5) ²

I = 0,025 kg m ²

4. piemērs. Gredzenu inerces moments ap asi, kas iet caur tās centru perpendikulāri riņķveida gredzena plaknei, ir 200 gm cm ² . Kāds būs inerces moments attiecībā uz tā diametru?

Risinājums:

Apļveida gredzena inerces moments ap asi, kas iet caur citu centru, kas ir perpendikulārs tā plaknei

MR ² = 200 gm cm ²

Inerces moments līdz diametram

= 1/2 MR ²

= 1/2 × 200 = 100 gm cm ²

Bieži uzdotie jautājumi par inerces mirkļiem

Kā aprēķināt inerces momentu?

Pamatformula jebkura vienveidīga objekta inerces momenta atrašanai ir:

Es = kungs ²

kur,
m ir objekta masa'
r ir attālums no rotācijas ass

Kā aprēķināt staru kūļa inerces momentu?

Stara inerces momentu pa centru un asi, kas tai horizontāli aprēķina, izmantojot formulu,

I = ML ² / 12

No kā ir atkarīgs ķermeņa inerces moments?

Jebkura objekta inerces moments ir atkarīgs no tālāk norādītajiem faktoriem:

• Ķermeņa masa,
• Rotācijas ass
• Objekta forma un izmērs

Kas ir inerces momenta vienība?

Inerces momenta mērvienība ir Kgm ²

Vai inerces moments var būt negatīvs?

Nē, inerces moments nekad nevar būt negatīvs.

Kas ir masas inerces moments?

Masas inerces moments ir ķermeņa pretestības mērījums pret tā leņķiskā impulsa vai virziena izmaiņām. Masas inerces momentu punktveida masai nosaka ar I = mr ² un daļiņu sistēmai masas inerces moments ir dots kā I = Σ _i m _i r _i ²

Kas ir apgabala inerces moments?

Laukuma inerces moments ir 2D formas plaknes īpašums, kas parāda, kā punkti tiek izkliedēti attiecībā pret patvaļīgu asi plaknē. Apgabala inerces moments ir pazīstams arī kā apgabala otrais moments vai laukuma kvadrātiskais moments. Formula laukuma inerces momentam xy plaknē ir dota kā I _xy = ∫xy dxdxy = ∫xy dA