Loģistiskā regresija R programmēšanā

Loģistiskā regresija R programmēšanā ir klasifikācijas algoritms, ko izmanto, lai noteiktu notikuma veiksmes un notikuma neveiksmes varbūtību. Loģistisko regresiju izmanto, ja atkarīgais mainīgais ir binārs (0/1, patiess/nepatiess, jā/nē). Logit funkcija tiek izmantota kā saites funkcija binomiālā sadalījumā.
Binārā iznākuma mainīgā lieluma varbūtību var paredzēt, izmantojot statistiskās modelēšanas paņēmienu, kas pazīstams kā loģistikas regresija. To plaši izmanto daudzās dažādās nozarēs, tostarp mārketingā, finansēs, sociālajās zinātnēs un medicīnas pētniecībā.
Loģistikas funkcija, ko parasti dēvē par sigmoīdo funkciju, ir loģistikas regresijas pamatideja. Šo sigmoīdo funkciju izmanto loģistikas regresijā, lai aprakstītu korelāciju starp prognozēšanas mainīgajiem un binārā iznākuma iespējamību.

Loģistiskā regresija R programmēšanā
Loģistiskā regresija ir pazīstama arī kā Binomiālā loģistikas regresija . Tas ir balstīts uz sigmoid funkciju, kur izvade ir varbūtība un ievade var būt no -bezgalības līdz +bezgalībai.
Teorija
Loģistikas regresija ir pazīstama arī kā vispārināts lineārs modelis. Tā kā to izmanto kā klasifikācijas paņēmienu, lai prognozētu kvalitatīvu reakciju, y vērtība svārstās no 0 līdz 1, un to var attēlot ar šādu vienādojumu:

Loģistiskā regresija R programmēšanā
lpp ir interesējošā rakstura varbūtība. Izredzes koeficients tiek definēts kā veiksmes varbūtība salīdzinājumā ar neveiksmes varbūtību. Tas ir galvenais loģistikas regresijas koeficientu attēlojums, un tam var būt vērtības no 0 līdz bezgalībai. Izredzes attiecība ir 1, ja veiksmes varbūtība ir vienāda ar neveiksmes varbūtību. Izredzes koeficients 2 ir tad, ja veiksmes varbūtība ir divreiz lielāka par neveiksmes varbūtību. Izredzes koeficients 0,5 ir tad, ja neveiksmes varbūtība ir divreiz lielāka par veiksmes iespējamību.
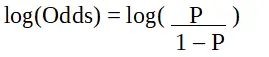
Loģistiskā regresija R programmēšanā
Tā kā mēs strādājam ar binomiālu sadalījumu (atkarīgo mainīgo), mums ir jāizvēlas saišu funkcija, kas ir vislabāk piemērota šim sadalījumam.
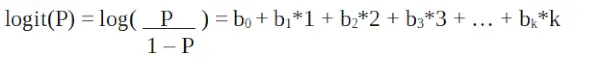
Loģistiskā regresija R programmēšanā
Tas ir logit funkcija . Iepriekš minētajā vienādojumā iekavas ir izvēlētas, lai palielinātu izlases vērtību novērošanas iespējamību, nevis samazinātu kļūdu kvadrātu summu (piemēram, parastā regresija). Logit ir pazīstams arī kā izredžu žurnāls. Logit funkcijai jābūt lineāri saistītai ar neatkarīgiem mainīgajiem. Tas ir no vienādojuma A, kur kreisā puse ir x lineāra kombinācija. Tas ir līdzīgs OLS pieņēmumam, ka y ir lineāri saistīts ar x. Mainīgie lielumi b0, b1, b2 … utt. nav zināmi, un tie ir jānovērtē, pamatojoties uz pieejamajiem apmācības datiem. Loģistiskās regresijas modelī, reizinot b1 ar vienu vienību, logit mainās ar b0. P izmaiņas vienas vienības izmaiņu dēļ būs atkarīgas no vērtības, kas reizināta. Ja b1 ir pozitīvs, tad P palielināsies un, ja b1 ir negatīvs, tad P samazināsies.
Datu kopa
mtcars (motoru tendenču auto ceļa tests) ietver degvielas patēriņu, veiktspēju un 10 automobiļu dizaina aspektus 32 automašīnām. Tas ir iepriekš instalēts ar dplyr iepakojums R.
R
# Installing the package> install.packages> (> 'dplyr'> )> # Loading package> library> (dplyr)> # Summary of dataset in package> summary> (mtcars)> |
Loģistikas regresijas veikšana datu kopā
Loģistiskā regresija tiek realizēta R, izmantojot glm() apmācot modeli, izmantojot datu kopas funkcijas vai mainīgos.
R
# Installing the package> # For Logistic regression> install.packages> (> 'caTools'> )> # For ROC curve to evaluate model> install.packages> (> 'ROCR'> )> > # Loading package> library> (caTools)> library> (ROCR)> |
Datu sadalīšana
R
# Splitting dataset> split <-> sample.split> (mtcars, SplitRatio = 0.8)> split> train_reg <-> subset> (mtcars, split ==> 'TRUE'> )> test_reg <-> subset> (mtcars, split ==> 'FALSE'> )> # Training model> logistic_model <-> glm> (vs ~ wt + disp,> > data = train_reg,> > family => 'binomial'> )> logistic_model> # Summary> summary> (logistic_model)> |
Izvade:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(> --- Signif. kodi: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Dispersijas parametrs binomiālajai ģimenei, kas pieņemts kā 1) Nulles novirze: 34,617 uz 24 brīvības pakāpēm Atlikusī novirze: 21 uz 20 22 brīvības pakāpes AIC: 26,212 Fišera punktu skaita iterāciju skaits: 6
- Izsaukums: tiek parādīts funkcijas izsaukums, kas tiek izmantots loģistikas regresijas modelim, kā arī informācija par ģimeni, formulu un datiem. Deviance Residuals: tie ir novirzes atlikumi, kas nosaka modeļa piemērotības pakāpi. Tie apzīmē neatbilstības starp faktiskajām atbildēm un loģistikas regresijas modeļa prognozēto varbūtību. Koeficienti: šie loģistikas regresijas koeficienti atspoguļo atbildes mainīgā loga izredzes vai logit. Standarta kļūdas, kas saistītas ar aprēķinātajiem koeficientiem, ir parādītas Std. Kļūdu kolonna. Nozīmīguma kodi: katra prognozējamā mainīgā nozīmīguma līmeni norāda ar nozīmīguma kodiem. Izkliedes parametrs: loģistiskajā regresijā dispersijas parametrs kalpo kā binomiālā sadalījuma mērogošanas parametrs. Šajā gadījumā tas ir iestatīts uz 1, norādot, ka pieņemtā dispersija ir 1. Nulles novirze: Nulles novirze aprēķina modeļa novirzi, ja tiek ņemta vērā tikai pārtveršana. Tas simbolizē novirzi, kas rastos no modeļa bez prognozēm. Atlikusī novirze: atlikušā novirze aprēķina modeļa novirzi pēc prognozētāju uzstādīšanas. Tas apzīmē atlikušo novirzi pēc prognozētāju ņemšanas vērā. AIC: Akaike informācijas kritērijs (AIC), kas atspoguļo prognozētāju skaitu, ir modeļa piemērotības rādītājs. Tas soda sarežģītākus modeļus, lai novērstu pārmērīgu pielāgošanu. Par labāk pieguļošiem modeļiem norāda zemākas AIC vērtības. Fišera vērtēšanas iterāciju skaits: iterāciju skaits, kas nepieciešams Fišera vērtēšanas procedūrai, lai novērtētu modeļa parametrus, tiek norādīts ar iterāciju skaitu.
Prognozējiet testa datus, pamatojoties uz modeli
R
predict_reg <-> predict> (logistic_model,> > test_reg, type => 'response'> )> predict_reg> |
Izvade:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943
R
# Changing probabilities> predict_reg <-> ifelse> (predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table> (test_reg$vs, predict_reg)> missing_classerr <-> mean> (predict_reg != test_reg$vs)> print> (> paste> (> 'Accuracy ='> , 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <-> prediction> (predict_reg, test_reg$vs)> ROCPer <-> performance> (ROCPred, measure => 'tpr'> ,> > x.measure => 'fpr'> )> auc <-> performance> (ROCPred, measure => 'auc'> )> auc <- [email protected][[1]]> auc> # Plotting curve> plot> (ROCPer)> plot> (ROCPer, colorize => TRUE> ,> > print.cutoffs.at => seq> (0.1, by = 0.1),> > main => 'ROC CURVE'> )> abline> (a = 0, b = 1)> auc <-> round> (auc, 4)> legend> (.6, .4, auc, title => 'AUC'> , cex = 1)> |
Izvade:
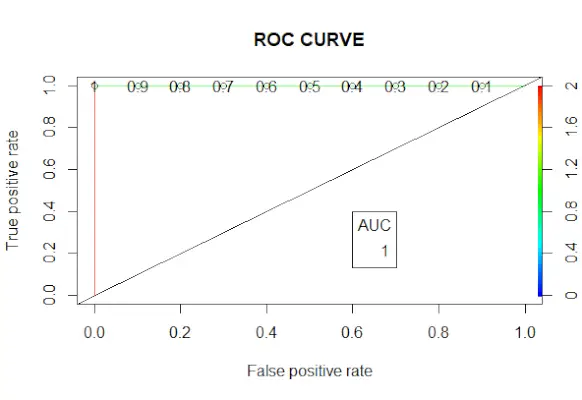
ROC līkne
2. piemērs:
Mēs varam veikt loģistikas regresijas modeļa Titānika datu kopu R.
R
# Load the dataset> data> (Titanic)> # Convert the table to a data frame> data <-> as.data.frame> (Titanic)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary> (model)> |
Izvade:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Pārtvert) 4,022e-16 8,660e-01 0 1 Class2nd -9,762e-16 1,000e+00 0 1 Class3. 00 0 1 DzimumsSieviete -3,140e-16 7,071e-01 0 1 Vecums Pieaugušais 5,103e-16 7,071e-01 0 1 (Izkliedes parametrs binomiālajai ģimenei pieņemts kā 1) Nulle novirze: 44,1361 brīvības novirze 1.6.6. uz 26 brīvības pakāpēm AIC: 56,361 Fišera punktu skaita iterāciju skaits: 2
Uzzīmējiet Titānika datu kopas ROC līkni
R
# Install and load the required packages> install.packages> (> 'ROCR'> )> library> (ROCR)> # Fit the logistic regression model> model <-> glm> (Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <-> predict> (model, type => 'response'> )> # Create a prediction object for ROCR> prediction_objects <-> prediction> (predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <-> performance> (prediction_obj, measure => 'tpr'> , x.measure => 'fpr'> )> # Plot the ROC curve> plot> (roc_object, main => 'ROC Curve'> , col => 'blue'> , lwd = 2)> # Add labels and a legend to the plot> legend> (> 'bottomright'> , legend => > paste> (> 'AUC ='> ,> round> (> performance> (prediction_objects, measure => 'auc'> )> > @y.values[[1]], 2)), col => 'blue'> , lwd = 2)> |
Izvade:
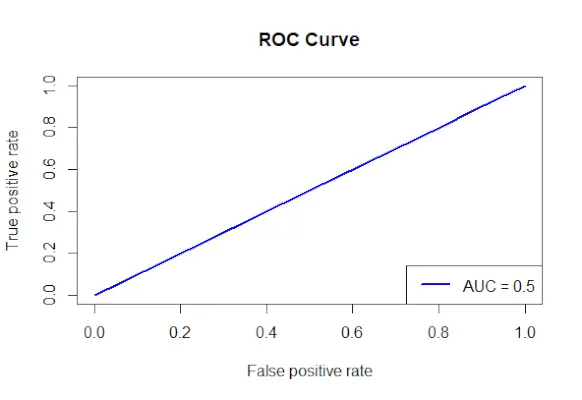
ROC līkne
- Izdzīvojušo prognozēšanai izmantotie faktori ir precizēti, un formula Izdzīvoja klase + dzimums + vecums tiek izmantota, lai izveidotu loģistikas regresijas modeli.
- Izmantojot prognožu () funkciju, prognozes tiek veiktas datu kopā, izmantojot pielāgoto modeli.
- Prognozētās varbūtības tiek apvienotas ar faktiskajām iznākuma vērtībām, lai izveidotu prognozēšanas objektu, izmantojot prognozēšanas () metodi no ROCR pakotnes.
- Ir norādīts patiesā pozitīvā ātruma (tpr) mērs un kļūdaini pozitīvā ātruma (fpr) x-ass mērs, un tiek izveidots ROC līknes objekts, izmantojot funkciju performance () no ROCR pakotnes.
- ROC līknes objekts (roc_obj), kas norāda galveno nosaukumu, krāsu un līnijas platumu, tiek attēlots, izmantojot funkciju plot().
- Tas izmanto funkciju performance() ar mērījumu = auc, lai noteiktu AUC (apgabals zem līknes) vērtību, un diagrammai pievieno etiķetes un leģendu.