Šī apmācība ir iesācējiem draudzīgs ceļvedis datu struktūru un algoritmu apguve izmantojot Python. Šajā rakstā mēs apspriedīsim iebūvētās datu struktūras, piemēram, sarakstus, virknes, vārdnīcas utt., un dažas lietotāja definētas datu struktūras, piemēram, saistītie saraksti , koki , grafiki u.c., kā arī šķērsošanas, kā arī meklēšanas un šķirošanas algoritmus ar labu un labi izskaidrotu piemēru un prakses jautājumu palīdzību.

Saraksti

Python saraksti ir sakārtotas datu kolekcijas tāpat kā masīvi citās programmēšanas valodās. Tas ļauj sarakstā iekļaut dažāda veida elementus. Python List ieviešana ir līdzīga Vectors C++ vai ArrayList Java. Dārgā darbība ir elementa ievietošana vai dzēšana no saraksta sākuma, jo visi elementi ir jāpārvieto. Ievietošana un dzēšana saraksta beigās var kļūt dārga arī gadījumā, ja iepriekš piešķirtā atmiņa kļūst pilna.

Piemērs: Python saraksta izveide

List = [1, 2, 3, 'GFG', 2.3] print(List) 

[1, 2, 3, 'GFG', 2.3] 

Saraksta elementiem var piekļūt, izmantojot piešķirto indeksu. Saraksta python sākuma indeksā secība ir 0 un beigu indekss (ja ir N elementi) N-1.

Piemērs: Python saraksta darbības

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) 

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks 

Tuple

Python korteži ir līdzīgi sarakstiem, bet Tuples ir nemainīgs dabā, t.i., kad tas ir izveidots, to nevar mainīt. Tāpat kā sarakstā, arī Tuple var saturēt dažāda veida elementus.

Programmā Python korteži tiek izveidoti, ievietojot vērtību secību, kas atdalīta ar “komatu”, izmantojot vai neizmantojot iekavas datu secības grupēšanai.

Piezīme: Lai izveidotu viena elementa virkni, beigu komatam ir jābūt. Piemēram, (8,) izveidos virkni, kurā kā elements būs 8.

Piemērs: Python Tuple Operations

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) 

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 

Iestatīt

Python komplekts ir mainīga datu kolekcija, kas nepieļauj dublēšanos. Kopas pamatā tiek izmantotas, lai iekļautu dalības testēšanu un dublēto ierakstu novēršanu. Šajā procesā izmantotā datu struktūra ir jaukšana — populārs paņēmiens, lai vidēji O(1) veiktu ievietošanu, dzēšanu un šķērsošanu.

Ja vienā indeksa pozīcijā ir vairākas vērtības, vērtība tiek pievienota šai indeksa pozīcijai, lai izveidotu saistīto sarakstu. CPython komplekti tiek ieviesti, izmantojot vārdnīcu ar fiktīviem mainīgajiem, kur galvenās būtnes dalībnieki iestata ar lielāku laika sarežģītības optimizāciju.

Iestatījuma ieviešana:

Komplekti ar daudzām darbībām vienā HashTable:

Piemērs: Python Set Operations

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) 

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True 

Saldēti komplekti

Saldēti komplekti Python ir nemainīgi objekti, kas atbalsta tikai metodes un operatorus, kas rada rezultātu, neietekmējot iesaldēto kopu vai kopas, kurām tie tiek lietoti. Lai gan kopas elementus var mainīt jebkurā laikā, iesaldētās kopas elementi pēc izveides paliek nemainīgi.

Piemērs: Python Frozen komplekts

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') 

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) 

Stīga

Python stīgas ir nemainīgs baitu masīvs, kas attēlo unikoda rakstzīmes. Python nav rakstzīmju datu tipa, viena rakstzīme ir vienkārši virkne, kuras garums ir 1.

Piezīme: Tā kā virknes ir nemainīgas, virknes modificēšanas rezultātā tiks izveidota jauna kopija.

Piemērs: Python stīgu darbības

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) 

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s 

Vārdnīca

Python vārdnīca ir nesakārtota datu kolekcija, kas glabā datus atslēgas:vērtības pāra formātā. Tas ir kā hash tabulas jebkurā citā valodā ar laika sarežģītību O(1). Python vārdnīcas indeksācija tiek veikta ar taustiņu palīdzību. Tie ir jebkura veida jaukšanas veidi, t.i., objekti, kas nekad nevar mainīties, piemēram, virknes, skaitļi, korteži utt. Mēs varam izveidot vārdnīcu, izmantojot cirtainus iekavas ({}) vai vārdnīcas izpratni.

Piemērs: Python vārdnīcas darbības

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) 

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} 

Matrica

Matrica ir 2D masīvs, kurā katrs elements ir stingri vienāda izmēra. Lai izveidotu matricu, mēs izmantosim NumPy pakotne .

Piemērs: Python NumPy matricas operācijas

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) 

Izvade

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] 

Bytearray

Python Bytearray sniedz mainīgu veselu skaitļu secību diapazonā 0 <= x < 256.

Piemērs: Python Bytearray operācijas

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) 

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e') 

Saistītais saraksts

A saistītais saraksts ir lineāra datu struktūra, kurā elementi netiek glabāti blakus esošās atmiņas vietās. Saistītā saraksta elementi ir saistīti, izmantojot norādes, kā parādīts zemāk esošajā attēlā:

Saistīto sarakstu attēlo rādītājs uz saistītā saraksta pirmo mezglu. Pirmo mezglu sauc par galvu. Ja saistītais saraksts ir tukšs, galvas vērtība ir NULL. Katrs mezgls sarakstā sastāv no vismaz divām daļām:

• Dati
• Rādītājs (vai atsauce) uz nākamo mezglu

Piemērs: Saistītā saraksta definēšana programmā Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None 

Izveidosim vienkāršu saistīto sarakstu ar 3 mezgliem.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | null | | 3 | null |  +----+------+ +----+------+ +----+------+ ''' otrais.nākamais = trešais ; # Saistiet otro mezglu ar trešo mezglu ''' Tagad nākamais otrajam mezglam attiecas uz trešo. Tātad visi trīs mezgli ir saistīti.  liste.galva otrā trešdaļa | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null |  +----+------+ +----+------+ +----+------+ ''' 

Saistītā saraksta apceļošana

Iepriekšējā programmā mēs esam izveidojuši vienkāršu saistīto sarakstu ar trim mezgliem. Izbrauksim izveidoto sarakstu un izdrukāsim katra mezgla datus. Lai veiktu pārvietošanos, uzrakstīsim vispārējas nozīmes funkciju printList(), kas izdrukā jebkuru sarakstu.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList() 

1 2 3 

Vairāk rakstu par saistīto sarakstu

• Saistītā saraksta ievietošana
• Saistītā saraksta dzēšana (dotās atslēgas dzēšana)
• Saistītā saraksta dzēšana (atslēgas dzēšana dotajā pozīcijā)
• Saistītā saraksta garuma atrašana (iteratīvs un rekursīvs)
• Meklēt elementu saistītajā sarakstā (iteratīvs un rekursīvs)
• N-tais mezgls no saistītā saraksta beigām
• Apgriezt saistīto sarakstu

A kaudze ir lineāra datu struktūra, kas saglabā vienumus pēdējā ienākošā/pirmā ārā (LIFO) vai First-In/Last-Out (FILO) veidā. Kaudzē jauns elements tiek pievienots vienā galā un elements tiek noņemts tikai no šī gala. Ievietošanas un dzēšanas darbības bieži sauc par push un pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty 

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: [] 

Kā kaudze, rindā ir lineāra datu struktūra, kas glabā vienumus FIFO (First In First Out) veidā. Ja ir rinda, vispirms tiek noņemts vismazāk pievienotais vienums. Labs rindas piemērs ir jebkura resursa patērētāju rinda, kurā pirmais tiek apkalpots patērētājs, kurš bija pirmais.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty 

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements [] 

Prioritārās rindas ir abstraktas datu struktūras, kur katram rindas datiem/vērtībai ir noteikta prioritāte. Piemēram, aviokompānijās bagāža ar nosaukumu Business vai First Class pienāk agrāk nekā pārējā. Prioritātes rinda ir rindas paplašinājums ar tālāk norādītajiem rekvizītiem.

• Elements ar augstu prioritāti tiek izslēgts no rindas pirms elementa ar zemu prioritāti.
• Ja diviem elementiem ir vienāda prioritāte, tie tiek apkalpoti atbilstoši to secībai rindā.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] atgriezt vienumu, izņemot IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) manaRinda.ievietot(12) manaRinda.ievietot(1) manaRinda.ievietot(14) manaRinda.ievietot(7) print(manaRinda), bet ne manaRinda.isEmpty(): print(myQueue.delete()) 

12 1 14 7 14 12 7 1 

Kaudze

heapq modulis Python nodrošina kaudzes datu struktūru, ko galvenokārt izmanto, lai attēlotu prioritāro rindu. Šīs datu struktūras īpašība ir tāda, ka tā vienmēr dod mazāko elementu (min kaudze), kad vien elements tiek uzmests. Ikreiz, kad elementi tiek stumti vai izspiesti, kaudzes struktūra tiek saglabāta. Elements hep[0] katru reizi atgriež arī mazāko elementu. Tas atbalsta mazākā elementa ekstrakciju un ievietošanu O(log n) laikos.

Parasti kaudzes var būt divu veidu:

• Maksimālā kaudze: Max-Heap atslēgai, kas atrodas saknes mezglā, ir jābūt vislielākajai starp atslēgām, kas atrodas visās tā atslēgās. Tam pašam rekvizītam ir jābūt rekursīvi patiesam visiem šī binārā koka apakškokiem.
• Minimālā kaudze: Min-Heap atslēgai, kas atrodas saknes mezglā, ir jābūt minimālai starp atslēgām, kas atrodas visos tā pakārtotos. Tam pašam rekvizītam ir jābūt rekursīvi patiesam visiem šī binārā koka apakškokiem.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) 

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1 

Vairāk rakstu par Heap

• Binārā kaudze
• K’th lielākais elements masīvā
• K’th mazākais/lielākais elements nešķirotajā masīvā
• Kārtot gandrīz sakārtotu masīvu
• K-tā lielākā summa blakus esošais apakšgrupa
• Minimālā divu skaitļu summa, kas veidojas no masīva cipariem

Koks ir hierarhiska datu struktūra, kas izskatās šādi:

 tree  ----  j  <-- root  /   f k  /   a h z  <-- leaves 

Koka augšējo mezglu sauc par sakni, savukārt apakšējos mezglus vai mezglus bez bērniem sauc par lapu mezgliem. Mezglus, kas atrodas tieši zem mezgla, sauc par tā bērniem, un mezglus, kas atrodas tieši virs kaut kā, sauc par tā vecākiem.

A binārais koks ir koks, kura elementiem var būt gandrīz divi bērni. Tā kā katram binārā koka elementam var būt tikai 2 bērni, mēs tos parasti nosaucam par kreiso un labo bērnu. Binārā koka mezglā ir šādas daļas.

• Dati
• Rādītājs uz kreiso bērnu
• Norādiet uz pareizo bērnu

Piemērs: mezgla klases definēšana

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key 

Tagad izveidosim koku ar 4 mezgliem Python. Pieņemsim, ka koka struktūra izskatās šādi -

 tree  ----  1  <-- root  /   2 3   /  4 

Piemērs: datu pievienošana kokam

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None''' 

Koku šķērsošana

Kokus var šķērsot dažādos veidos. Tālāk ir norādīti parasti izmantotie koku šķērsošanas veidi. Apskatīsim zemāk esošo koku -

 tree  ----  1  <-- root  /   2 3   /  4 5 

Pirmās dziļuma šķērsošanas reizes:

• Kārtība (pa kreisi, sakne, pa labi): 4 2 5 1 3
• Iepriekšēja pasūtīšana (sakne, pa kreisi, pa labi): 1 2 4 5 3
• Postorder (pa kreisi, pa labi, sakne): 4 5 2 3 1

Algoritma secība (koks)

• Pārejiet pa kreiso apakškoku, t.i., izsauciet Inorder(kreisais apakškoks)
• Apmeklējiet sakni.
• Pārejiet pa labo apakškoku, t.i., izsauciet Inorder(labais-apakškoks)

Algoritma priekšpasūtīšana (koks)

• Apmeklējiet sakni.
• Pārejiet pa kreiso apakškoku, t.i., izsauciet Preorder(left-subtree)
• Pārejiet pa labo apakškoku, t.i., izsauciet Preorder(labais-apakškoks)

Algoritms Pasta pasūtījums (koks)

• Pārejiet pa kreiso apakškoku, t.i., izsauciet Postorder(left-subtree)
• Pārejiet pa labo apakškoku, t.i., izsauciet Postorder(labais-apakškoks)
• Apmeklējiet sakni.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) 

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1 

Laika sarežģītība — O(n)

Platuma pirmā vai līmeņa pasūtījuma izbraukšana

Līmeņa pasūtījuma šķērsošana koks ir koka šķērsošana platumā. Iepriekš minētā koka līmeņa secības šķērsošana ir 1 2 3 4 5.

Katram mezglam vispirms tiek apmeklēts mezgls un pēc tam tā pakārtotie mezgli tiek ievietoti FIFO rindā. Zemāk ir algoritms tam pašam -

• Izveidojiet tukšu rindu q
• temp_node = sakne /*sākt no saknes*/
• Cilpa, kamēr temp_node nav NULL
  • drukāt temp_node->data.
  • Ievietojiet temp_node bērnu rindas (vispirms kreiso, pēc tam labo atvasinājumu) uz q
  • Atvienojiet mezglu no q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Izdrukājiet rindas priekšpusi un # noņemiet to no rindas drukāšanas (rinda[0].data) node = queue.pop(0) # Iekļauts rindas kreisā bērnā, ja node.left nav Nav: queue.append(node.left ) # Iestatīt labo bērnu rindā, ja node.right nav Nav: queue.append(node.right) # Draiverprogramma, lai pārbaudītu iepriekš minēto funkciju root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Mezgls(4) root.left.right = Mezgls(5) print ('Līmeņa secības pārvietošanās binārā koka ir -') printLevelOrder(root) 

Level Order Traversal of binary tree is - 1 2 3 4 5 

Laika sarežģītība: O(n)

Vairāk rakstu par Bināro koku

• Ievietošana binārajā kokā
• Dzēšana binārajā kokā
• Kārtības koka šķērsošana bez rekursijas
• Inorder Tree Traversal bez rekursijas un bez kaudzes!
• Drukāt pēc pasūtījuma šķērsošanu no dotajiem pasūtījuma un priekšpasūtīšanas maršrutiem
• Atrodiet BST šķērsošanu pēc pasūtījuma no priekšpasūtīšanas

Binārais meklēšanas koks ir uz mezgliem balstīta binārā koka datu struktūra, kurai ir šādas īpašības:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val  < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key) 

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val  < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r) 

20 30 40 50 60 70 80 

A grafikā ir nelineāra datu struktūra, kas sastāv no mezgliem un malām. Mezgli dažreiz tiek saukti arī par virsotnēm, un malas ir līnijas vai loki, kas savieno jebkurus divus grafa mezglus. Formālāk grafiku var definēt kā grafiku, kas sastāv no ierobežotas virsotņu (vai mezglu) kopas un malu kopas, kas savieno mezglu pāri.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) 

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Draiveri programma iepriekšminētajai grafiku klasei if __name__ == '__main__' : V = 5 grafiks = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() 

Adjacency list of vertex 0 head ->4 -> 1 virsotnes blakus esošo saraksts 1 galva -> 4 -> 3 -> 2 -> 0 virsotnes blakus saraksts 2 galva -> 3 -> 1 virsotnes blakus saraksts 3 galva -> 4 -> 2 -> 1 blakus esošais punkts virsotņu saraksts 4 galva -> 3 -> 1 -> 0>>   
 Grafika šķērsošana  
 
 Breadth-First meklēšana vai BFS  
  
     Breadth-First Traversal    jo grafiks ir līdzīgs koka platuma šķērsošanai. Atšķirībā no kokiem, grafiki var saturēt ciklus, tāpēc mēs varam atkal nonākt pie tā paša mezgla. Lai izvairītos no mezgla apstrādes vairāk nekā vienu reizi, mēs izmantojam Būla apmeklēto masīvu. Vienkāršības labad tiek pieņemts, ka visas virsotnes ir sasniedzamas no sākuma virsotnes.  
  
 Piemēram, nākamajā grafikā mēs sākam šķērsošanu no 2. virsotnes. Kad nonākam līdz virsotnei 0, mēs meklējam visas tai blakus esošās virsotnes. 2 ir arī blakus virsotne ar 0. Ja mēs neatzīmēsim apmeklētās virsotnes, tad 2 tiks apstrādāts vēlreiz, un tas kļūs par procesu, kas nebeidzas. Sekojošā diagrammas pirmā šķērsošana platumā ir 2, 0, 3, 1.  
  
     
Python3   
# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) 
    
  Izvade    Laika sarežģītība: O(V+E), kur V ir grafa virsotņu skaits un E ir grafa malu skaits.  
  
 Pirmā dziļuma meklēšana vai DFS  
 
   Pirmā dziļuma šķērsošana    jo grafiks ir līdzīgs koka pirmajam dziļumam. Vienīgā fiksācija šeit ir tāda, ka atšķirībā no kokiem grafikos var būt cikli, mezglu var apmeklēt divas reizes. Lai izvairītos no mezgla apstrādes vairāk nekā vienu reizi, izmantojiet Būla apmeklēto masīvu.  
  
    Algoritms:     
  
 
 Izveidojiet rekursīvu funkciju, kas ņem mezgla indeksu un apmeklēto masīvu.  
 
 Atzīmējiet pašreizējo mezglu kā apmeklētu un izdrukājiet mezglu.  
 
 Pārvietojiet visus blakus esošos un neatzīmētos mezglus un izsauciet rekursīvo funkciju ar blakus esošā mezgla indeksu.  
 
Python3   
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) 
    
  Izvade   
Following is DFS from (starting from vertex 2) 2 0 1 3 
  
 Vairāk rakstu par grafiku  
 
 
  Grafiku attēlojumi, izmantojot kopu un jaucējfunkciju   
 
  Grafikā atrodiet mātes virsotni   
 
  Iteratīvā dziļuma pirmā meklēšana   
 
  Saskaitiet mezglu skaitu noteiktā līmenī kokā, izmantojot BFS   
 
  Saskaitiet visus iespējamos ceļus starp divām virsotnēm   
 
 
  Procesu, kurā funkcija tieši vai netieši izsauc sevi, sauc par rekursiju, un atbilstošo funkciju sauc par a    rekursīvā funkcija   . Izmantojot rekursīvos algoritmus, dažas problēmas var atrisināt diezgan vienkārši. Šādu problēmu piemēri ir Hanojas torņi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph utt.   
   
 Kāds ir rekursijas pamatnosacījums?  
 
 Rekursīvajā programmā tiek sniegts bāzes gadījuma risinājums un lielākās problēmas risinājums tiek izteikts mazāku uzdevumu izteiksmē.  
  
def fact(n):  # base case  if (n  <= 1)   return 1  else   return n*fact(n-1) 
 
 Iepriekš minētajā piemērā ir definēts bāzes gadījums n  <= 1, un lielāku skaitļa vērtību var atrisināt, konvertējot uz mazāku, līdz tiek sasniegts bāzes gadījums.  
  
 Kā atmiņa tiek piešķirta dažādiem funkciju izsaukumiem rekursijā?  
 
 Kad jebkura funkcija tiek izsaukta no main(), tai stekā tiek piešķirta atmiņa. Rekursīvā funkcija izsauc sevi, atmiņa izsauktajai funkcijai tiek piešķirta papildus izsaucējai funkcijai piešķirtajai atmiņai, un katram funkcijas izsaukumam tiek izveidota atšķirīga vietējo mainīgo kopija. Kad ir sasniegts bāzes gadījums, funkcija atgriež savu vērtību funkcijai, kas to izsauc, un atmiņa tiek atdalīta, un process turpinās.  
  
 Ņemsim piemēru, kā darbojas rekursija, izmantojot vienkāršu funkciju.  
Python3   
# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test  < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test) 
    
  Izvade   
3 2 1 1 2 3 
  
 Atmiņas kaudze ir parādīta zemāk esošajā diagrammā.  
  
  
  
 Vairāk rakstu par Rekursiju  
  
  
  Rekursija   
  
     Rekursija Python    
 
  Prakses jautājumi par rekursiju | 1. komplekts   
 
  Prakses jautājumi par rekursiju | 2. komplekts   
 
  Prakses jautājumi par rekursiju | 3. komplekts   
 
  Prakses jautājumi par rekursiju | 4. komplekts   
 
  Prakses jautājumi par rekursiju | 5. komplekts   
 
  Prakses jautājumi par rekursiju | 6. komplekts   
 
  Prakses jautājumi par rekursiju | 7. komplekts   
 
 
     >>> Vairāk      
  
    Dinamiskā programmēšana     
 
   Dinamiskā programmēšana    galvenokārt ir optimizācija, izmantojot vienkāršu rekursiju. Visur, kur mēs redzam rekursīvu risinājumu, kurā ir atkārtoti izsaukumi pēc vienas un tās pašas ievades, mēs varam to optimizēt, izmantojot dinamisko programmēšanu. Ideja ir vienkārši saglabāt apakšproblēmu rezultātus, lai mums tie vēlāk nebūtu jāpārrēķina, kad tas ir nepieciešams. Šī vienkāršā optimizācija samazina laika sarežģītību no eksponenciāla līdz polinomam. Piemēram, ja mēs rakstām vienkāršu rekursīvu risinājumu Fibonači skaitļiem, mēs iegūstam eksponenciālu laika sarežģītību un, ja mēs to optimizējam, saglabājot apakšproblēmu risinājumus, laika sarežģītība samazinās līdz lineārai.  
  
  
  
 Tabulēšana pret memoizāciju  
 
 Ir divi dažādi veidi, kā saglabāt vērtības, lai apakšproblēmas vērtības varētu izmantot atkārtoti. Šeit tiks apspriesti divi dinamiskās programmēšanas (DP) problēmas risināšanas modeļi:  
  
 
    Tabula:     No apakšas uz augšu  
 
    Memoization:     No augšas uz leju  
 
 
 Tabulēšana  
 
 Kā jau pats nosaukums liecina, sākt no apakšas un krāt atbildes uz augšu. Parunāsim par valsts pāreju.  
  
 Aprakstīsim mūsu DP problēmas stāvokli dp[x] ar dp[0] kā bāzes stāvokli un dp[n] kā galamērķa stāvokli. Tātad mums ir jāatrod galamērķa stāvokļa vērtība, t.i., dp[n].  
  
 Ja mēs sākam pāreju no mūsu bāzes stāvokļa, t.i., dp[0], un sekojam mūsu stāvokļa pārejas attiecībai, lai sasniegtu galamērķa stāvokli dp[n], mēs to saucam par pieeju no apakšas uz augšu, jo ir pilnīgi skaidrs, ka mēs sākām pāreju no apakšējo bāzes stāvokli un sasniedza augstāko vēlamo stāvokli.  
  
 Tagad, kāpēc mēs to saucam par tabulēšanas metodi?  
  
 Lai to zinātu, vispirms uzrakstīsim kodu, lai aprēķinātu skaitļa faktoriālu, izmantojot augšupēju pieeju. Kā vispārējo procedūru DP risināšanai mēs atkal definējam stāvokli. Šajā gadījumā mēs definējam stāvokli kā dp[x], kur dp[x] ir, lai atrastu x faktoriālu.  
  
 Tagad ir pilnīgi skaidrs, ka dp[x+1] = dp[x] * (x+1)  
  
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i 
 
 Memoizācija  
 
 Vēlreiz aprakstīsim to stāvokļa pārejas izteiksmē. Ja mums ir jāatrod kāda stāvokļa vērtība, sakiet dp[n] un tā vietā, lai sāktu no bāzes stāvokļa, t.i., dp[0], mēs prasām atbildi no stāvokļiem, kas pēc stāvokļa pārejas var sasniegt galamērķa stāvokli dp[n]. attiecības, tad tā ir DP mode no augšas uz leju.  
  
 Šeit mēs sākam savu ceļojumu no augstākā galamērķa stāvokļa un aprēķinām tā atbildi, saskaitot to stāvokļu vērtības, kas var sasniegt galamērķa stāvokli, līdz sasniedzam zemāko bāzes stāvokli.  
  
 Vēlreiz rakstīsim faktoriālās problēmas kodu lejupejošā veidā  
  
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1)) 
 
  
  
 Vairāk rakstu par dinamisko programmēšanu  
 
 
  Optimāla apakšstruktūras īpašība   
 
  Pārklāšanās apakšproblēmu īpašums   
 
   Fibonači skaitļi    
 
  Apakškopa ar summu, kas dalās ar m   
 
  Maksimālā summa, kas palielina secību   
 
  Garākā kopējā apakšvirkne   
 
 
      >>> Vairāk       
  
 Meklēšanas algoritmi  
 
 Lineārā meklēšana  
 
 
 Sāciet no arr[] vistālāk kreisā elementa un pa vienam salīdziniet x ar katru elementu arr[]  
 
 Ja x atbilst elementam, atgrieziet indeksu.  
 
 Ja x neatbilst nevienam no elementiem, atgriež -1.  
 
  
     
Python3   
# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) 
    
  Izvade   
Element is present at index 3 
  
 Iepriekš minētā algoritma laika sarežģītība ir O(n).  
  
 Lai iegūtu papildinformāciju, skatiet   Lineārā meklēšana   .  
  
 Binārā meklēšana  
 
 Meklējiet sakārtotā masīvā, atkārtoti dalot meklēšanas intervālu uz pusēm. Sāciet ar intervālu, kas aptver visu masīvu. Ja meklēšanas taustiņa vērtība ir mazāka par vienumu intervāla vidū, sašauriniet intervālu līdz apakšējai pusei. Pretējā gadījumā sašauriniet to līdz augšējai pusei. Atkārtoti pārbaudiet, līdz tiek atrasta vērtība vai intervāls ir tukšs.  
  
     
Python3   
# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Ja elements atrodas pašā vidū if arr[mid] == x: return mid # Ja elements ir mazāks par vidu, tad tas # var būt tikai kreisajā apakšgrupā elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Citādi elements var atrasties tikai # labajā apakšgrupā else: return binarySearch(arr, mid + 1, r, x ) else: # Elements nav masīvā return -1 # Draivera kods arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funkcijas izsaukuma rezultāts = binarySearch(arr, 0, len(arr)-1 , x) ja rezultāts != -1: drukāt ('Elements atrodas indeksā % d' % rezultāts) else: print ('Elements nav masīvā') 
    
  Izvade   
Element is present at index 3 
  
 Iepriekš minētā algoritma laika sarežģītība ir O(log(n)).  
  
 Lai iegūtu papildinformāciju, skatiet    Binārā meklēšana    .  
  
 Šķirošanas algoritmi  
 
 Atlase Kārtot  
 
 The    atlases kārtošana    algoritms sašķiro masīvu, atkārtoti atrodot minimālo elementu (ņemot vērā augošo secību) no nešķirotās daļas un ievietojot to sākumā. Katrā atlases kārtošanas iterācijā tiek atlasīts minimālais elements (ņemot vērā augošo secību) no nešķirotā apakšgrupas un pārvietots uz sakārtoto apakšgrupu.  
  
 Atlases kārtošanas blokshēma:  
  
     
Python3   
# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Apmainiet atrasto minimālo elementu ar # pirmo elementu A[i], A[min_idx] = A[min_idx], A[i] # Pārbaudāmais draivera kods virs drukas ('Sorted array ') i diapazonā (len(A)): drukāt ('%d' %A[i]), 
    
  Izvade   
Sorted array 11 12 22 25 64 
  
    Laika sarežģītība:     O(n   2   ), jo ir divas ligzdotas cilpas.  
  
    Palīgtelpa:     O(1)  
  
 Burbuļu kārtošana  
 
   Burbuļu kārtošana    ir vienkāršākais kārtošanas algoritms, kas darbojas, atkārtoti apmainot blakus esošos elementus, ja tie atrodas nepareizā secībā.  
  
    Ilustrācija :     
  
     
Python3   
# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Pārbaudāmais draivera kods iepriekš arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Sorted array is:') for i in range(len(arr)): print ('%d' %arr[i]), 
    
  Izvade   
Sorted array is: 11 12 22 25 34 64 90 
  
    Laika sarežģītība:     O(n   2   )  
  
 Ievietošanas kārtošana  
 
 Lai kārtotu n izmēra masīvu augošā secībā, izmantojot    ievietošanas kārtošana    :  
  
 
 Atkārtojiet no arr[1] līdz arr[n] pa masīvu.  
 
 Salīdziniet pašreizējo elementu (atslēgu) ar tā priekšgājēju.  
 
 Ja galvenais elements ir mazāks par tā priekšgājēju, salīdziniet to ar iepriekšējiem elementiem. Pārvietojiet lielākos elementus par vienu pozīciju uz augšu, lai atbrīvotu vietu apmainītajam elementam.  
 
 
    Ilustrācija:     
  
     
Python3   
# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 un atslēga < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) 
    
  Izvade   
 5 6 11 12 13 
  
    Laika sarežģītība:     O(n   2   ))  
  
 Sapludināt Kārtot  
 
 Tāpat kā QuickSort,    Sapludināt Kārtot    ir sadalīt un iekarot algoritms. Tas sadala ievades masīvu divās daļās, izsauc sevi par divām daļām un pēc tam apvieno abas sakārtotās daļas. Funkciju sapludināšana() izmanto divu daļu sapludināšanai. Apvienošana (arr, l, m, r) ir galvenais process, kurā tiek pieņemts, ka arr[l..m] un arr[m+1..r] ir sakārtoti, un apvieno abus sakārtotos apakšmasīvus vienā.  
  
MergeSort(arr[], l, r) If r>l 1. Atrodiet vidējo punktu, lai sadalītu masīvu divās daļās: vidus m = l+ (r-l)/2 2. Izsaukt mergeSort pirmajai pusei: Call mergeSort(arr, l, m) 3. Call mergeSort for second half: Call mergeSort(arr, m+1, r) 4. Apvienojiet abas puses, kas sakārtotas 2. un 3. darbībā: izsauciet merge(arr, l, m, r) 
  
     
Python3   
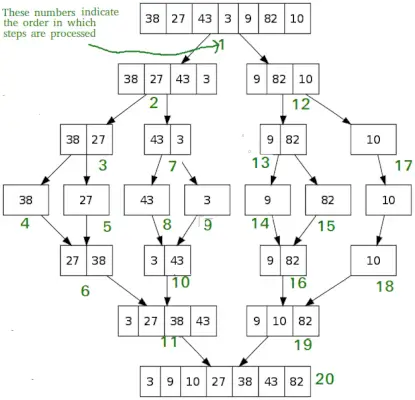
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Masīva vidusdaļas atrašana mid = len(arr)//2 # Masīva elementu L = arr[:mid] # sadalīšana 2 daļās R = arr[mid:] # Pirmās puses kārtošana mergeSort(L) # Otrās puses kārtošana mergeSort(R) i = j = k = 0 # Kopēt datus pagaidu masīvos L[] un R[], kamēr i < len(L) and j  < len(R): if L[i]  < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i  < len(L): arr[k] = L[i] i += 1 k += 1 while j  < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) 
    
  Izvade   
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13 
  
    Laika sarežģītība:     O(n(logn))  
  
 QuickSort  
 
 Tāpat kā sapludināšanas kārtošana,    QuickSort    ir sadalīt un iekarot algoritms. Tas izvēlas elementu kā šarnīra punktu un sadala doto masīvu ap izvēlēto pivotu. Ir daudz dažādu QuickSort versiju, kas izvēlas pagriezienu dažādos veidos.  
  
 Vienmēr izvēlieties pirmo elementu kā rakursu.  
  
 
 Vienmēr izvēlieties pēdējo elementu kā rakursu (ieviests tālāk)  
 
 Izvēlieties izlases elementu kā rakursu.  
 
 Izvēlieties vidējo kā rakursu.  
 
 
 QuickSort galvenais process ir partition (). Sadalījumu mērķis ir, ja tiek dots masīvs un masīva elements x kā pagrieziena punkts, sakārtotajā masīvā novieto x pareizajā vietā un visus mazākos elementus (mazākus par x) novieto pirms x un visus lielākos elementus (lielākus par x) pēc. x. Tas viss jādara lineārā laikā.  
  
/* low -->Sākuma indekss, augsts --> beigu indekss */ quickSort(arr[], zems, augsts) { if (low { /* pi ir sadalīšanas indekss, arr[pi] tagad atrodas pareizajā vietā */ pi = partition(arr, zems, augsts);  
  
  
    Sadalīšanas algoritms     
  
 Sadalīšanas veikšanai var būt daudz veidu, sekojot    pseido kods    izmanto CLRS grāmatā norādīto metodi. Loģika ir vienkārša, mēs sākam no vistālāk kreisā elementa un sekojam mazāku (vai vienādu) elementu indeksam kā i. Braucot, ja atrodam mazāku elementu, pašreizējo elementu apmainām ar arr[i]. Pretējā gadījumā mēs ignorējam pašreizējo elementu.  
  pivot: end -= 1 # Ja sākums un beigas nav krustojušies, # apmainiet sākuma un beigu skaitļus if(sākums < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start  < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') 
    
  Izvade   
Sorted array: [1, 5, 7, 8, 9, 10] 
  
    Laika sarežģītība:     O(n(logn))  
  
 ShellSort  
 
  ShellSort   galvenokārt ir ievietošanas kārtošanas variants. Ievietošanas kārtošanā elementi tiek pārvietoti tikai vienu pozīciju uz priekšu. Ja elements ir jāpārvieto tālu uz priekšu, ir iesaistītas daudzas kustības. ShellSort ideja ir ļaut apmainīties ar tālu vienumiem. Programmā shellSort mēs sakārtojam masīvu h pēc lielas h vērtības. Mēs turpinām samazināt h vērtību, līdz tā kļūst par 1. Tiek uzskatīts, ka masīvs ir sakārtots pēc h, ja visi katra h apakšsaraksti   th   elements ir sakārtots.  
Python3   
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = atstarpe # pārbaudiet masīvu no kreisās puses uz labo # līdz pēdējam iespējamajam j indeksam, kamēr j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # tagad, mēs atskatāmies no i-tā indeksa pa kreisi # mēs apmainām vērtības, kuras nav pareizā secībā. k = i, kamēr k - sprauga> -1: ja arr[k - sprauga]> arr[k]: arr[k-atstarpe],arr[k] = arr[k],arr[k-atstarpe] k -= 1 sprauga //= 2 # draiveris, lai pārbaudītu kodu arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2)>>   
  Izvade       Laika sarežģītība:     O(n   2   ).