EIKLĪDA ALGORITMI (PAMATA UN PAPLAŠINĀTIE) - TECHCODEVIEW.COM

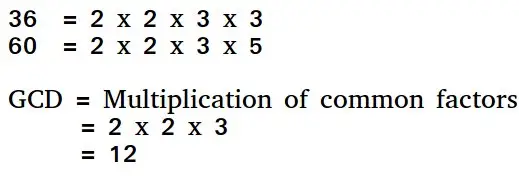
Eiklīda algoritms ir veids, kā atrast divu pozitīvu veselu skaitļu lielāko kopīgo dalītāju. Divu skaitļu GCD ir lielākais skaitlis, kas dala tos abus. Vienkāršs veids, kā atrast GCD, ir faktorizēt gan skaitļus, gan reizināt kopējos primāros faktorus.

GCD

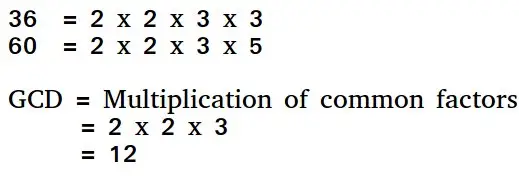
Pamata Eiklīda algoritms GCD:

Algoritms ir balstīts uz tālāk norādītajiem faktiem.

Ja mēs atņemam mazāku skaitli no lielāka (mēs samazinām lielāku skaitli), GCD nemainās. Tātad, ja mēs pastāvīgi atņemam lielāko no diviem, mēs nonākam pie GCD.
Tagad atņemšanas vietā, ja sadalām mazāko skaitli, algoritms apstājas, kad atrodam atlikušo 0.

Zemāk ir rekursīva funkcija, lai novērtētu gcd, izmantojot Eiklida algoritmu:

C

// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 35, b = 10;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > a = 31, b = 2;> > printf> (>

'GCD(%d, %d) = %d
'>

, a, b, gcd(a, b));> > return> 0;> }>

CPP

// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(> int> a,> int> b)> {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> }> // Driver Code> int> main()> {> > int> a = 10, b = 15;> > > // Function call> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 35, b = 10;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > a = 31, b = 2;> > cout < <> 'GCD('> < < a < <> ', '> < < b < <> ') = '> < < gcd(a, b)> > < < endl;> > return> 0;> }>

Java

// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> > // extended Euclidean Algorithm> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a ==> 0> )> > return> b;> > return> gcd(b % a, a);> > }> > // Driver code> > public> static> void> main(String[] args)> > {> > int> a => 10> , b => 15> , g;> > > // Function call> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 35> ;> > b => 10> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a => 31> ;> > b => 2> ;> > g = gcd(a, b);> > System.out.println(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // Code Contributed by Mohit Gupta_OMG>

Python3

# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> > if> a> => => 0> :> > return> b> > return> gcd(b> %> a, a)> # Driver code> if> __name__> => => '__main__'> :> > a> => 10> > b> => 15> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 35> > b> => 10> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> > a> => 31> > b> => 2> > print> (> 'gcd('> , a,> ','> , b,> ') = '> , gcd(a, b))> # Code Contributed By Mohit Gupta_OMG>

C#

// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> > public> static> int> gcd(> int> a,> int> b)> > {> > if> (a == 0)> > return> b;> > return> gcd(b % a, a);> > }> > // Driver Code> > static> public> void> Main()> > {> > int> a = 10, b = 15, g;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 35;> > b = 10;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > a = 31;> > b = 2;> > g = gcd(a, b);> > Console.WriteLine(> 'GCD('> + a +> ' , '> + b> > +> ') = '> + g);> > }> }> // This code is contributed by ajit>

PHP

// php program to demonstrate Basic Euclidean Algorithm>

 // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) {  if ($a == 0)  return $b;  return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ',   gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ',   gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ',   gcd($a, $b); // This code is contributed by m_kit ?>>>

>    
      
      
       
   
       
       
     
     
   
          // JavaScript program to demonstrate>   // Basic Euclidean Algorithm>   // Function to return>   // gcd of a and b>   function>   gcd( a, b)>   {>   >  if>   (a == 0)>   >  return>   b;>   >  return>   gcd(b % a, a);>   }>   // Driver Code>   >  let a = 10, b = 15;>   >  document.write(>  'GCD('>   + a +>  ', '>   >  + b +>  ') = '>   + gcd(a, b) +>  ' '>  );>   >   >  a = 35, b = 10;>   >  document.write(>  'GCD('>   + a +>  ', '>   >  + b +>  ') = '>   + gcd(a, b) +>  ' '>  );>   >   >  a = 31, b = 2;>   >  document.write(>  'GCD('>   + a +>  ', '>   >  + b +>  ') = '>   + gcd(a, b) +>  ' '>  );>   // This code contributed by aashish1995>     
  
  
   
      
    
      
    
  Izvade    
  GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1 
    Laika sarežģītība: O(Žurn. min(a, b)) 
  Palīgtelpa: O(žurnāls (min(a,b)) 
    Paplašinātais Eiklīda algoritms:   
    Paplašinātais Eiklīda algoritms atrod arī veselu skaitļu koeficientus x un y tā, ka: ax + by = gcd(a, b) 
  
    Piemēri:   
      Ievade: a = 30, b = 20 
  Izvade: gcd = 10, x = 1, y = -1 
(Ņemiet vērā, ka 30*1 + 20*(-1) = 10) 
    Ievade: a = 35, b = 15 
  Izvade: gcd = 5, x = 1, y = -2 
(Ņemiet vērā, ka 35*1 + 15*(-2) = 5) 
  
  Paplašinātais Eiklīda algoritms atjaunina gcd(a, b) rezultātus, izmantojot rezultātus, kas aprēķināti ar rekursīvo izsaukumu gcd(b%a, a). Ļaujiet x un y vērtībām, kas aprēķinātas ar rekursīvo zvanu, ir x ₁un y ₁. x un y tiek atjaunināti, izmantojot tālāk norādītās izteiksmes. 
    ax + by = gcd(a, b) 
gcd(a, b) = gcd(b%a, a) 
gcd(b%a, a) = (b%a)x ₁+ ir ₁  
ax + ar = (b%a)x ₁+ ir ₁  
ax + by = (b – [b/a] * a)x ₁+ ir ₁  
ax + by = a(y ₁– [b/a] * x ₁) + bx ₁ 
  Salīdzinot LHS un RHS, 
x = y ₁- ?ba? *x ₁  
y = x ₁ 
  
Ieteicamā prakse paplašinātais eiklīda algoritms Izmēģiniet to! Tālāk ir sniegta iepriekš minētās pieejas īstenošana. 
  C++ 
      
       
   
       
       
     
     
   
          // C++ program to demonstrate working of>   // extended Euclidean Algorithm>   #include>   using>   namespace>   std;>   // Function for extended Euclidean Algorithm>   int>   gcdExtended(>  int>   a,>  int>   b,>  int>   *x,>  int>   *y)>   {>   >  // Base Case>   >  if>   (a == 0)>   >  {>   >  *x = 0;>   >  *y = 1;>   >  return>   b;>   >  }>   >  int>   x1, y1;>  // To store results of recursive call>   >  int>   gcd = gcdExtended(b%a, a, &x1, &y1);>   >  // Update x and y using results of>   >  // recursive call>   >  *x = y1 - (b/a) * x1;>   >  *y = x1;>   >  return>   gcd;>   }>   // Driver Code>   int>   main()>   {>   >  int>   x, y, a = 35, b = 15;>   >  int>   g = gcdExtended(a, b, &x, &y);>   >  cout  < <>  'GCD('>    < < a  < <>  ', '>    < < b>   >   < <>  ') = '>    < < g  < < endl;>   >  return>   0;>   }>     
  
  
   
      
    
      
    
  C 
      
       
   
       
       
     
     
   
          // C program to demonstrate working of extended>   // Euclidean Algorithm>   #include>   // C function for extended Euclidean Algorithm>   int>   gcdExtended(>  int>   a,>  int>   b,>  int>   *x,>  int>   *y)>   {>   >  // Base Case>   >  if>   (a == 0)>   >  {>   >  *x = 0;>   >  *y = 1;>   >  return>   b;>   >  }>   >  int>   x1, y1;>  // To store results of recursive call>   >  int>   gcd = gcdExtended(b%a, a, &x1, &y1);>   >  // Update x and y using results of recursive>   >  // call>   >  *x = y1 - (b/a) * x1;>   >  *y = x1;>   >  return>   gcd;>   }>   // Driver Program>   int>   main()>   {>   >  int>   x, y;>   >  int>   a = 35, b = 15;>   >  int>   g = gcdExtended(a, b, &x, &y);>   >  printf>  (>  'gcd(%d, %d) = %d'>  , a, b, g);>   >  return>   0;>   }>     
  
  
   
      
    
      
    
  Java 
      
       
   
       
       
     
     
   
          // Java program to demonstrate working of extended>   // Euclidean Algorithm>   import>   java.lang.*;>   import>   java.util.*;>   class>   GFG {>   >  // extended Euclidean Algorithm>   >  public>   static>   int>   gcdExtended(>  int>   a,>  int>   b,>  int>   x,>   >  int>   y)>   >  {>   >  // Base Case>   >  if>   (a ==>  0>  ) {>   >  x =>  0>  ;>   >  y =>  1>  ;>   >  return>   b;>   >  }>   >  int>   x1 =>  1>  ,>   >  y1 =>  1>  ;>  // To store results of recursive call>   >  int>   gcd = gcdExtended(b % a, a, x1, y1);>   >  // Update x and y using results of recursive>   >  // call>   >  x = y1 - (b / a) * x1;>   >  y = x1;>   >  return>   gcd;>   >  }>   >  // Driver Program>   >  public>   static>   void>   main(String[] args)>   >  {>   >  int>   x =>  1>  , y =>  1>  ;>   >  int>   a =>  35>  , b =>  15>  ;>   >  int>   g = gcdExtended(a, b, x, y);>   >  System.out.print(>  'gcd('>   + a +>  ' , '>   + b>   >  +>  ') = '>   + g);>   >  }>   }>     
  
  
   
      
    
      
    
  Python3 
      
       
   
       
       
     
     
   
          # Python program to demonstrate working of extended>   # Euclidean Algorithm>   # function for extended Euclidean Algorithm>   def>   gcdExtended(a, b):>   >  # Base Case>   >  if>   a>  =>  =>   0>  :>   >  return>   b,>  0>  ,>  1>   >  gcd, x1, y1>  =>   gcdExtended(b>  %>   a, a)>   >  # Update x and y using results of recursive>   >  # call>   >  x>  =>   y1>  ->   (b>  />  />  a)>  *>   x1>   >  y>  =>   x1>   >  return>   gcd, x, y>   # Driver code>   a, b>  =>   35>  ,>  15>   g, x, y>  =>   gcdExtended(a, b)>   print>  (>  'gcd('>  , a,>  ','>  , b,>  ') = '>  , g)>     
  
  
   
      
    
      
    
  C# 
      
       
   
       
       
     
     
   
          // C# program to demonstrate working>   // of extended Euclidean Algorithm>   using>   System;>   class>   GFG>   {>   >   >  // extended Euclidean Algorithm>   >  public>   static>   int>   gcdExtended(>  int>   a,>  int>   b,>   >  int>   x,>  int>   y)>   >  {>   >  // Base Case>   >  if>   (a == 0)>   >  {>   >  x = 0;>   >  y = 1;>   >  return>   b;>   >  }>   >  // To store results of>   >  // recursive call>   >  int>   x1 = 1, y1 = 1;>   >  int>   gcd = gcdExtended(b % a, a, x1, y1);>   >  // Update x and y using>   >  // results of recursive call>   >  x = y1 - (b / a) * x1;>   >  y = x1;>   >  return>   gcd;>   >  }>   >   >  // Driver Code>   >  static>   public>   void>   Main ()>   >  {>   >  int>   x = 1, y = 1;>   >  int>   a = 35, b = 15;>   >  int>   g = gcdExtended(a, b, x, y);>   >  Console.WriteLine(>  'gcd('>   + a +>  ' , '>   +>   >  b +>  ') = '>   + g);>   >  }>   }>     
  
  
   
      
    
      
    
  PHP 
      
       
   
       
       
     
     
   
           // PHP program to demonstrate  // working of extended  // Euclidean Algorithm // PHP function for  // extended Euclidean  // Algorithm function gcdExtended($a, $b,   $x, $y) {  // Base Case  if ($a == 0)  {  $x = 0;  $y = 1;  return $b;  }  // To store results   // of recursive call  $gcd = gcdExtended($b % $a,   $a, $x, $y);  // Update x and y using  // results of recursive  // call  $x = $y - floor($b / $a) * $x;  $y = $x;  return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>>>    
  
  
   
      
  >    
      
      
       
   
       
       
     
     
   
          >   // Javascript program to demonstrate>   // working of extended>   // Euclidean Algorithm>   // Javascript function for>   // extended Euclidean>   // Algorithm>   function>   gcdExtended(a, b,>   >  x, y)>   {>   >  // Base Case>   >  if>   (a == 0)>   >  {>   >  x = 0;>   >  y = 1;>   >  return>   b;>   >  }>   >  // To store results>   >  // of recursive call>   >  let gcd = gcdExtended(b % a,>   >  a, x, y);>   >  // Update x and y using>   >  // results of recursive>   >  // call>   >  x = y - (b / a) * x;>   >  y = x;>   >  return>   gcd;>   }>   // Driver Code>   let x = 0;>   let y = 0;>   let a = 35;>   let b = 15;>   let g = gcdExtended(a, b, x, y);>   document.write(>  'gcd('>   + a);>   document.write(>  ', '>   + b +>  ')'>  );>   document.write(>  ' = '>   + g);>   >     
  
  
   
      
    
      
    
    Izvade:   
  gcd(35, 15) = 5 
    Laika sarežģītība: O(log N) 
  Palīgtelpa: O(log N) 
    Kā darbojas paplašinātais algoritms?   
    Kā redzams iepriekš, x un y ir ievades a un b rezultāti, 
  a.x + b.y = gcd —-(1) 
  Un x ₁un y ₁ir rezultāti ievadei b%a un a 
  (b%a).x ₁+ a.y ₁= gcd 
  Ja iepriekš ievietojam b%a = (b – (?b/a?).a), 
mēs sekojam. Ņemiet vērā, ka ?b/a? ir stāvs (b/a) 
  (b – (?b/a?).a).x ₁+ a.y ₁= gcd 
  Iepriekš minēto vienādojumu var uzrakstīt arī šādi 
  b.x ₁+ a.(un ₁– (?b/a?).x ₁) = gcd — (2) 
  Pēc “a” un “b” koeficientu salīdzināšanas (1) un 
(2), mēs sekojam, 
x = y ₁- ?ba? *x ₁  
y = x ₁ 
  
    Kā paplašinātais algoritms ir noderīgs?   
  Paplašinātais Eiklīda algoritms ir īpaši noderīgs, ja a un b ir koprime (vai gcd ir 1). Tā kā x ir moduļa b modulārais reizināšanas inverss, un y ir b moduļa a modulārais reizināšanas inverss. Jo īpaši modulārās reizināšanas apgrieztās vērtības aprēķināšana ir būtisks solis RSA publiskās atslēgas šifrēšanas metodē.