N-veida koka diametrs
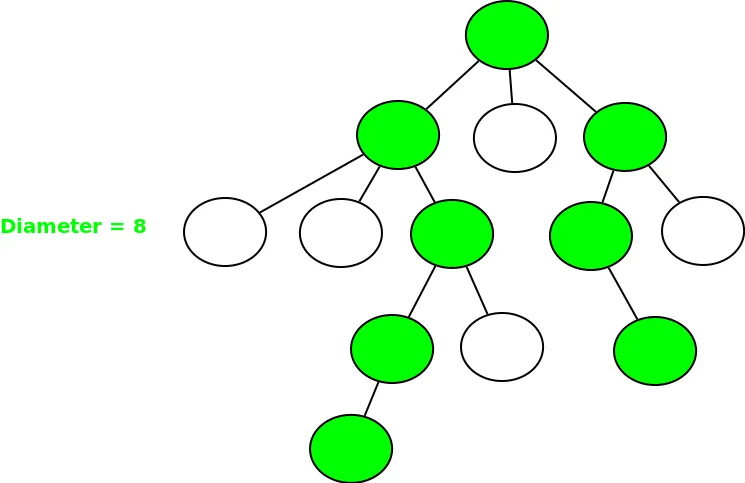
N-veida koka diametrs ir garākais ceļš starp jebkuriem diviem koka mezgliem. Šiem diviem mezgliem jābūt diviem lapu mezgliem. Tālāk norādītajos piemēros ir iekrāsots garākais ceļš[diametrs].
1. piemērs:

2. piemērs:

Priekšnosacījums: Binārā koka diametrs .
Ceļš var sākties no viena no mezgliem un iet uz augšu uz vienu no šo mezglu LCA un atkal nonākt līdz kāda cita apakškoka dziļākajam mezglam. vai var pastāvēt kā viena no pašreizējā mezgla atvasinātajām vērtībām.
Risinājums pastāvēs jebkurā no šiem:
- Diametrs vienam no pašreizējā mezgla bērniem
- Augstāko divu apakškoku augstuma summa + 1
Īstenošana:
C++ // C++ program to find the height of an N-ary // tree #include using namespace std ; // Structure of a node of an n-ary tree struct Node { char key ; vector < Node *> child ; }; // Utility function to create a new tree node Node * newNode ( int key ) { Node * temp = new Node ; temp -> key = key ; return temp ; } // Utility function that will return the depth // of the tree int depthOfTree ( struct Node * ptr ) { // Base case if ( ! ptr ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) maxdepth = max ( maxdepth depthOfTree ( * it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree int diameter ( struct Node * ptr ) { // Base case if ( ! ptr ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) { int h = depthOfTree ( * it ); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) maxChildDia = max ( maxChildDia diameter ( * it )); return max ( maxChildDia max1 + max2 + 1 ); } // Driver program int main () { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node * root = newNode ( 'A' ); ( root -> child ). push_back ( newNode ( 'B' )); ( root -> child ). push_back ( newNode ( 'F' )); ( root -> child ). push_back ( newNode ( 'D' )); ( root -> child ). push_back ( newNode ( 'E' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'K' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'J' )); ( root -> child [ 2 ] -> child ). push_back ( newNode ( 'G' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'C' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'H' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'I' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'N' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'M' )); ( root -> child [ 3 ] -> child [ 2 ] -> child ). push_back ( newNode ( 'L' )); cout < < diameter ( root ) < < endl ; return 0 ; }
Java // Java program to find the height of an N-ary // tree import java.util.* ; class GFG { // Structure of a node of an n-ary tree static class Node { char key ; Vector < Node > child ; }; // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new Vector < Node > (); return temp ; } // Utility function that will return the depth // of the tree static int depthOfTree ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth for ( Node it : ptr . child ) maxdepth = Math . max ( maxdepth depthOfTree ( it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( Node it : ptr . child ) { int h = depthOfTree ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; for ( Node it : ptr . child ) maxChildDia = Math . max ( maxChildDia diameter ( it )); return Math . max ( maxChildDia max1 + max2 + 1 ); } // Driver Code public static void main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node root = newNode ( 'A' ); ( root . child ). add ( newNode ( 'B' )); ( root . child ). add ( newNode ( 'F' )); ( root . child ). add ( newNode ( 'D' )); ( root . child ). add ( newNode ( 'E' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'K' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'J' )); ( root . child . get ( 2 ). child ). add ( newNode ( 'G' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'C' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'H' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'I' )); ( root . child . get ( 0 ). child . get ( 0 ). child ). add ( newNode ( 'N' )); ( root . child . get ( 0 ). child . get ( 0 ). child ). add ( newNode ( 'M' )); ( root . child . get ( 3 ). child . get ( 2 ). child ). add ( newNode ( 'L' )); System . out . print ( diameter ( root ) + 'n' ); } } // This code is contributed by Rajput-Ji
Python3 # Python program to find the height of an N-ary # tree # Structure of a node of an n-ary tree class Node : def __init__ ( self x ): self . key = x self . child = [] # Utility function that will return the depth # of the tree def depthOfTree ( ptr ): # Base case if ( not ptr ): return 0 maxdepth = 0 # Check for all children and find # the maximum depth for it in ptr . child : maxdepth = max ( maxdepth depthOfTree ( it )) return maxdepth + 1 # Function to calculate the diameter # of the tree def diameter ( ptr ): # Base case if ( not ptr ): return 0 # Find top two highest children max1 max2 = 0 0 for it in ptr . child : h = depthOfTree ( it ) if ( h > max1 ): max2 max1 = max1 h elif ( h > max2 ): max2 = h # Iterate over each child for diameter maxChildDia = 0 for it in ptr . child : maxChildDia = max ( maxChildDia diameter ( it )) return max ( maxChildDia max1 + max2 + 1 ) # Driver program if __name__ == '__main__' : # /* Let us create below tree # * A # * / / # * B F D E # * / | /| # * K J G C H I # * / # * N M L # */ root = Node ( 'A' ) ( root . child ) . append ( Node ( 'B' )) ( root . child ) . append ( Node ( 'F' )) ( root . child ) . append ( Node ( 'D' )) ( root . child ) . append ( Node ( 'E' )) ( root . child [ 0 ] . child ) . append ( Node ( 'K' )) ( root . child [ 0 ] . child ) . append ( Node ( 'J' )) ( root . child [ 2 ] . child ) . append ( Node ( 'G' )) ( root . child [ 3 ] . child ) . append ( Node ( 'C' )) ( root . child [ 3 ] . child ) . append ( Node ( 'H' )) ( root . child [ 3 ] . child ) . append ( Node ( 'I' )) ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'N' )) ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'M' )) ( root . child [ 3 ] . child [ 2 ] . child ) . append ( Node ( 'L' )) print ( diameter ( root )) # This code is contributed by mohit kumar 29
C# // C# program to find the height of // an N-ary tree using System ; using System.Collections.Generic ; class GFG { // Structure of a node of an n-ary tree class Node { public char key ; public List < Node > child ; }; // Utility function to create // a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new List < Node > (); return temp ; } // Utility function that will return // the depth of the tree static int depthOfTree ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth foreach ( Node it in ptr . child ) maxdepth = Math . Max ( maxdepth depthOfTree ( it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; foreach ( Node it in ptr . child ) { int h = depthOfTree ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; foreach ( Node it in ptr . child ) maxChildDia = Math . Max ( maxChildDia diameter ( it )); return Math . Max ( maxChildDia max1 + max2 + 1 ); } // Driver Code public static void Main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node root = newNode ( 'A' ); ( root . child ). Add ( newNode ( 'B' )); ( root . child ). Add ( newNode ( 'F' )); ( root . child ). Add ( newNode ( 'D' )); ( root . child ). Add ( newNode ( 'E' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'K' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'J' )); ( root . child [ 2 ]. child ). Add ( newNode ( 'G' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'C' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'H' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). Add ( newNode ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). Add ( newNode ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). Add ( newNode ( 'L' )); Console . Write ( diameter ( root ) + 'n' ); } } // This code is contributed by Rajput-Ji
JavaScript < script > // Javascript program to find the // height of an N-ary tree // Structure of a node of an n-ary tree class Node { // Utility function to create a new tree node constructor ( key ) { this . key = key ; this . child = []; } } // Utility function that will // return the depth // of the tree function depthOfTree ( ptr ) { // Base case if ( ptr == null ) return 0 ; let maxdepth = 0 ; // Check for all children and find // the maximum depth for ( let it = 0 ; it < ptr . child . length ; it ++ ) maxdepth = Math . max ( maxdepth depthOfTree ( ptr . child [ it ])); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree function diameter ( ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children let max1 = 0 max2 = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) { let h = depthOfTree ( ptr . child [ it ]); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter let maxChildDia = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) maxChildDia = Math . max ( maxChildDia diameter ( ptr . child [ it ])); return Math . max ( maxChildDia max1 + max2 + 1 ); } // Driver Code /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ let root = new Node ( 'A' ); ( root . child ). push ( new Node ( 'B' )); ( root . child ). push ( new Node ( 'F' )); ( root . child ). push ( new Node ( 'D' )); ( root . child ). push ( new Node ( 'E' )); ( root . child [ 0 ]. child ). push ( new Node ( 'K' )); ( root . child [ 0 ]. child ). push ( new Node ( 'J' )); ( root . child [ 2 ]. child ). push ( new Node ( 'G' )); ( root . child [ 3 ]. child ). push ( new Node ( 'C' )); ( root . child [ 3 ]. child ). push ( new Node ( 'H' )); ( root . child [ 3 ]. child ). push ( new Node ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). push ( new Node ( 'L' )); document . write ( diameter ( root ) + 'n' ); // This code is contributed by patel2127 < /script>
Izvade
7
- Laika sarežģītība: O(N)
- Telpas sarežģītība: O(N)
Iepriekšminētā risinājuma optimizācijas: Mēs varam atrast diametru, neaprēķinot koka dziļumu, veicot nelielas izmaiņas iepriekš minētajā risinājumā, līdzīgi kā binārā koka diametra atrašanā.
Īstenošana:
C++ // C++ program to find the height of an N-ary // tree #include using namespace std ; // Structure of a node of an n-ary tree struct Node { char key ; vector < Node *> child ; }; // Utility function to create a new tree node Node * newNode ( int key ) { Node * temp = new Node ; temp -> key = key ; return temp ; } int diameter ( struct Node * ptr int & diameter_of_tree ) { // Base case if ( ! ptr ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) { int h = diameter ( * it diameter_of_tree ); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Find whether our node can be part of diameter diameter_of_tree = max ( max1 + max2 + 1 diameter_of_tree ); return max ( max1 max2 ) + 1 ; } int main () { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node * root = newNode ( 'A' ); ( root -> child ). push_back ( newNode ( 'B' )); ( root -> child ). push_back ( newNode ( 'F' )); ( root -> child ). push_back ( newNode ( 'D' )); ( root -> child ). push_back ( newNode ( 'E' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'K' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'J' )); ( root -> child [ 2 ] -> child ). push_back ( newNode ( 'G' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'C' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'H' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'I' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'N' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'M' )); ( root -> child [ 3 ] -> child [ 2 ] -> child ). push_back ( newNode ( 'L' )); // for storing diameter int diameter_of_tree = 0 ; diameter ( root diameter_of_tree ); cout < < diameter_of_tree < < endl ; return 0 ; } // This code is improved by bhuvan
Java // Java program to find the height of an N-ary // tree import java.util.* ; class GFG { // Structure of a node of an n-ary tree static class Node { char key ; Vector < Node > child ; }; // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new Vector < Node > (); return temp ; } // for storing diameter_of_tree public static int diameter_of_tree = 0 ; // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( Node it : ptr . child ) { int h = diameter ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } diameter_of_tree = Math . max ( max1 + max2 + 1 diameter_of_tree ); return ( Math . max ( max1 max2 ) + 1 ); } // Driver Code public static void main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node root = newNode ( 'A' ); ( root . child ). add ( newNode ( 'B' )); ( root . child ). add ( newNode ( 'F' )); ( root . child ). add ( newNode ( 'D' )); ( root . child ). add ( newNode ( 'E' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'K' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'J' )); ( root . child . get ( 2 ). child ). add ( newNode ( 'G' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'C' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'H' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'I' )); ( root . child . get ( 0 ). child . get ( 0 ). child ) . add ( newNode ( 'N' )); ( root . child . get ( 0 ). child . get ( 0 ). child ) . add ( newNode ( 'M' )); ( root . child . get ( 3 ). child . get ( 2 ). child ) . add ( newNode ( 'L' )); diameter ( root ); System . out . print ( diameter_of_tree + 'n' ); } } // This code is improved by Bhuvan
Python3 # Python3 program to find the height of an N-ary # tree # Structure of a node of an n-ary tree # Structure of a node of an n-ary tree class Node : # Utility function to create a tree node def __init__ ( self key ): self . key = key ; self . child = []; diameter_of_tree = 0 ; def diameter ( ptr ): global diameter_of_tree # Base case # Base case if ( ptr == None ): return 0 ; # Find top two highest children max1 = 0 max2 = 0 ; for it in range ( len ( ptr . child )): h = diameter ( ptr . child [ it ]); if ( h > max1 ): max2 = max1 max1 = h ; elif ( h > max2 ): max2 = h ; # Find whether our node can be part of diameter diameter_of_tree = max ( max1 + max2 + 1 diameter_of_tree ); return max ( max1 max2 ) + 1 ; def main (): ''' us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L ''' root = Node ( 'A' ); ( root . child ) . append ( Node ( 'B' )); ( root . child ) . append ( Node ( 'F' )); ( root . child ) . append ( Node ( 'D' )); ( root . child ) . append ( Node ( 'E' )); ( root . child [ 0 ] . child ) . append ( Node ( 'K' )); ( root . child [ 0 ] . child ) . append ( Node ( 'J' )); ( root . child [ 2 ] . child ) . append ( Node ( 'G' )); ( root . child [ 3 ] . child ) . append ( Node ( 'C' )); ( root . child [ 3 ] . child ) . append ( Node ( 'H' )); ( root . child [ 3 ] . child ) . append ( Node ( 'I' )); ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'N' )); ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'M' )); ( root . child [ 3 ] . child [ 2 ] . child ) . append ( Node ( 'L' )); diameter ( root ); print ( diameter_of_tree ); main () # This code is contributed by phasing17.
C# // C# program to find the height of an N-ary // tree using System ; using System.Collections.Generic ; // Structure of a node of an n-ary tree class Node { public char key ; public List < Node > child ; }; class GFG { // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new List < Node > (); return temp ; } // for storing diameter_of_tree public static int diameter_of_tree = 0 ; // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; foreach ( Node it in ptr . child ) { int h = diameter ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } diameter_of_tree = Math . Max ( max1 + max2 + 1 diameter_of_tree ); return ( Math . Max ( max1 max2 ) + 1 ); } // Driver Code public static void Main ( string [] args ) { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node root = newNode ( 'A' ); ( root . child ). Add ( newNode ( 'B' )); ( root . child ). Add ( newNode ( 'F' )); ( root . child ). Add ( newNode ( 'D' )); ( root . child ). Add ( newNode ( 'E' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'K' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'J' )); ( root . child [ 2 ]. child ). Add ( newNode ( 'G' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'C' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'H' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ) . Add ( newNode ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ) . Add ( newNode ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ) . Add ( newNode ( 'L' )); diameter ( root ); Console . Write ( diameter_of_tree + 'n' ); } } // This code is improved by phasing17
JavaScript // Javascript program to find the height of an N-ary // tree // Structure of a node of an n-ary tree // Structure of a node of an n-ary tree class Node { // Utility function to create a new tree node constructor ( key ) { this . key = key ; this . child = []; } } let diameter_of_tree = 0 ; function diameter ( ptr ) { // Base case // Base case if ( ptr == null ) return 0 ; // Find top two highest children let max1 = 0 max2 = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) { let h = diameter ( ptr . child [ it ]); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Find whether our node can be part of diameter diameter_of_tree = Math . max ( max1 + max2 + 1 diameter_of_tree ); return Math . max ( max1 max2 ) + 1 ; } /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ let root = new Node ( 'A' ); ( root . child ). push ( new Node ( 'B' )); ( root . child ). push ( new Node ( 'F' )); ( root . child ). push ( new Node ( 'D' )); ( root . child ). push ( new Node ( 'E' )); ( root . child [ 0 ]. child ). push ( new Node ( 'K' )); ( root . child [ 0 ]. child ). push ( new Node ( 'J' )); ( root . child [ 2 ]. child ). push ( new Node ( 'G' )); ( root . child [ 3 ]. child ). push ( new Node ( 'C' )); ( root . child [ 3 ]. child ). push ( new Node ( 'H' )); ( root . child [ 3 ]. child ). push ( new Node ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). push ( new Node ( 'L' )); diameter ( root diameter_of_tree ); console . log ( diameter_of_tree ); // This code is contributed by garg28harsh.
Izvade
7
- Laika sarežģītība: O(N^2)
- Palīgtelpa: O(N+H) kur N ir mezglu skaits kokā un H ir koka augstums.
Cits optimizēts risinājums: Garākais ceļš nevirzītā kokā
Vēl viena pieeja diametra iegūšanai DFS vienā pārgājienā:
Koka diametru var aprēķināt tāpat kā katram mezglam
- Pašreizējais mezgls nav daļa no diametra (t.i., diametrs atrodas vienā no pašreizējā mezgla atvasinājumiem).
- Pašreizējais mezgls ir daļa no diametra (t.i., diametrs iet caur pašreizējo mezglu).
Mezgls: Blakus esošo vietu saraksts ir izmantots koka uzglabāšanai.
Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.
C++ // C++ implementation to find // diameter of a tree using // DFS in ONE TRAVERSAL #include using namespace std ; #define maxN 10005 // The array to store the // height of the nodes int height [ maxN ]; // Adjacency List to store // the tree vector < int > tree [ maxN ]; // variable to store diameter // of the tree int diameter = 0 ; // Function to add edge between // node u to node v void addEdge ( int u int v ) { // add edge from u to v tree [ u ]. push_back ( v ); // add edge from v to u tree [ v ]. push_back ( u ); } void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node for ( auto u : tree [ cur ]) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = max ( height [ cur ] height [ u ]); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ]; } else if ( height [ u ] > max2 ) { max2 = height [ u ]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = max ( diameter height [ cur ]); diameter = max ( diameter max1 + max2 + 1 ); } // Driver Code int main () { // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); cout < < 'Diameter of tree is : ' < < diameter - 1 < < ' n ' ; return 0 ; }
Java /*package whatever //do not write package name here */ import java.io.* ; import java.util.* ; class GFG { static int maxN = 10005 ; // The array to store the // height of the nodes static int [] height = new int [ maxN ] ; // Adjacency List to store // the tree static ArrayList < ArrayList < Integer >> tree = new ArrayList < ArrayList < Integer >> (); // variable to store diameter // of the tree static int diameter = 0 ; // Function to add edge between // node u to node v static void addEdge ( int u int v ) { // add edge from u to v tree . get ( u ). add ( v ); // add edge from v to u tree . get ( v ). add ( u ); } static void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node for ( int u : tree . get ( cur )) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = Math . max ( height [ cur ] height [ u ] ); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ] ; } else if ( height [ u ] > max2 ) { max2 = height [ u ] ; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . max ( diameter height [ cur ] ); diameter = Math . max ( diameter max1 + max2 + 1 ); } public static void main ( String [] args ) { for ( int i = 0 ; i < maxN ; i ++ ) { tree . add ( new ArrayList < Integer > ()); } // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); System . out . println ( 'Diameter of tree is : ' + ( diameter - 1 )); } } // This code is contributed by ab2127.
Python3 # C++ implementation to find # diameter of a tree using # DFS in ONE TRAVERSAL maxN = 10005 # The array to store the # height of the nodes height = [ 0 for i in range ( maxN )] # Adjacency List to store # the tree tree = [[] for i in range ( maxN )] # variable to store diameter # of the tree diameter = 0 # Function to add edge between # node u to node v def addEdge ( u v ): # add edge from u to v tree [ u ] . append ( v ) # add edge from v to u tree [ v ] . append ( u ) def dfs ( cur par ): global diameter # Variables to store the height of children # of cur node with maximum heights max1 = 0 max2 = 0 # going in the adjacency list of the current node for u in tree [ cur ]: # if that node equals parent discard it if ( u == par ): continue # calling dfs for child node dfs ( u cur ) # calculating height of nodes height [ cur ] = max ( height [ cur ] height [ u ]) # getting the height of children # of cur node with maximum height if ( height [ u ] >= max1 ): max2 = max1 max1 = height [ u ] elif ( height [ u ] > max2 ): max2 = height [ u ] height [ cur ] += 1 # Diameter of a tree can be calculated as # diameter passing through the node # diameter doesn't includes the cur node diameter = max ( diameter height [ cur ]) diameter = max ( diameter max1 + max2 + 1 ) # Driver Code # n is the number of nodes in tree n = 7 # Adding edges to the tree addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 1 4 ) addEdge ( 2 5 ) addEdge ( 4 6 ) addEdge ( 4 7 ) # Calling the dfs function to # calculate the diameter of tree dfs ( 1 0 ) print ( 'Diameter of tree is :' diameter - 1 ) # This code is contributed by avanitrachhadiya2155
C# using System ; using System.Collections.Generic ; class GFG { static int maxN = 10005 ; // The array to store the // height of the nodes static int [] height = new int [ maxN ]; // Adjacency List to store // the tree static List < List < int >> tree = new List < List < int >> (); // variable to store diameter // of the tree static int diameter = 0 ; // Function to Add edge between // node u to node v static void AddEdge ( int u int v ) { // Add edge from u to v tree [ u ]. Add ( v ); // Add edge from v to u tree [ v ]. Add ( u ); } static void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node foreach ( int u in tree [ cur ]) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = Math . Max ( height [ cur ] height [ u ]); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ]; } else if ( height [ u ] > max2 ) { max2 = height [ u ]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . Max ( diameter height [ cur ]); diameter = Math . Max ( diameter max1 + max2 + 1 ); } public static void Main ( string [] args ) { for ( int i = 0 ; i < maxN ; i ++ ) { tree . Add ( new List < int > ()); } // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree AddEdge ( 1 2 ); AddEdge ( 1 3 ); AddEdge ( 1 4 ); AddEdge ( 2 5 ); AddEdge ( 4 6 ); AddEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); Console . WriteLine ( 'Diameter of tree is : ' + ( diameter - 1 )); } } // This code is contributed by phasing17.
JavaScript < script > // Javascript implementation to find // diameter of a tree using // DFS in ONE TRAVERSAL let maxN = 10005 ; // The array to store the // height of the nodes let height = new Array ( maxN ); // Adjacency List to store // the tree let tree = new Array ( maxN ); for ( let i = 0 ; i < maxN ; i ++ ) { height [ i ] = 0 ; tree [ i ] = []; } // variable to store diameter // of the tree let diameter = 0 ; // Function to add edge between // node u to node v function addEdge ( u v ) { // add edge from u to v tree [ u ]. push ( v ); // add edge from v to u tree [ v ]. push ( u ); } function dfs ( cur par ) { // Variables to store the height of children // of cur node with maximum heights let max1 = 0 ; let max2 = 0 ; // going in the adjacency list // of the current node for ( let u = 0 ; u < tree [ cur ]. length ; u ++ ) { // if that node equals parent discard it if ( tree [ cur ][ u ] == par ) continue ; // calling dfs for child node dfs ( tree [ cur ][ u ] cur ); // calculating height of nodes height [ cur ] = Math . max ( height [ cur ] height [ tree [ cur ][ u ]]); // getting the height of children // of cur node with maximum height if ( height [ tree [ cur ][ u ]] >= max1 ) { max2 = max1 ; max1 = height [ tree [ cur ][ u ]]; } else if ( height [ tree [ cur ][ u ]] > max2 ) { max2 = height [ tree [ cur ][ u ]]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . max ( diameter height [ cur ]); diameter = Math . max ( diameter max1 + max2 + 1 ); } // Driver Code // n is the number of nodes in tree let n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); document . write ( 'Diameter of tree is : ' + ( diameter - 1 )) // This code is contributed by unknown2108 < /script>
Izvade
Diameter of tree is : 4
- Laika sarežģītība: O(N) Kur N ir mezglu skaits dotajā binārajā kokā.
- Palīgtelpa: O(N)