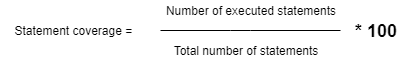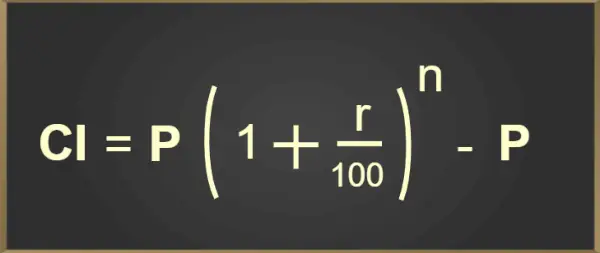
Saliktie procenti ir procenti, kas tiek aprēķināti pret aizdevuma vai noguldījuma summu, kurā tiek aprēķināti procenti par pamatsummu, kā arī iepriekš nopelnītajiem procentiem.

Kopējā atšķirība starp saliktajiem un vienkāršajiem procentiem ir tā, ka saliktie procenti , procenti tiek aprēķināti par pamatsummu, kā arī par iepriekš nopelnītajiem procentiem, savukārt vienkāršie procenti ir atkarīgi tikai no ieguldītās pamatsummas.

Satura rādītājs

• Kas ir saliktie procenti?
• Salikto procentu formula
• Kā aprēķināt saliktos procentus?
• Salikto procentu formula — atvasināšana
• Pusgada salikto procentu formula
• Ceturkšņa salikto procentu formula
• Mēneša salikto procentu formula
• Ikdienas salikto procentu formula
• Periodiskās savienošanas ātruma formula
• 72. noteikums
• Saliktās procentu likmes vairākus gadus pēc kārtas
• Nepārtrauktas procentu formulas
• Daži citi saliktas nozīmes lietojumi
• Atšķirība starp saliktajiem procentiem un vienkāršiem procentiem
• Salikto procentu piemēri
• Saliktās intereses — prakses jautājumi

Kas ir saliktie procenti?

Saliktie procenti ir procenti par pamatsummu, kā arī procenti, kas nopelnīti par pamatsummu. Vārds saliktās procentu likmes sastāv no diviem vārdiem Savienojums, kas nozīmē, ka sastāv no diviem vai vairākiem, un procenti nozīmē naudu, kas nopelnīta, aizdodot summu. Tādējādi saliktie procenti ir nauda, ​​​​kas nopelnīta par aizdevumu, un tos veido divu veidu procenti, kas ir:

• Procenti par pamatsummu

• Procenti par procentiem, kas nopelnīti par pamatsummu periodā

Salikto procentu definīcija

Saliktie procenti ir procenti, kas aprēķināti par pamatsummu un iepriekš nopelnītie procenti. To apzīmē ar C.I. Tas ir ļoti noderīgi investīciju un kredīta atmaksas nolūkos. To sauc arī par procentu procentiem.

Saliktie procenti ir ļoti noderīgs banku un finanšu sektorā un ir noderīgs arī citās nozarēs. Daži no tā lietojumiem ir:

• Valsts iedzīvotāju skaita pieaugums
• Investīciju vērtība noteiktā laika periodā.
• Lai atrastu jebkura izstrādājuma palielinātās izmaksas un nolietoto vērtību.
• Jebkuras institūcijas vai valsts izaugsmes prognozēšanai.

Saliktie procenti (C.I) = summa — pamatsumma

Salikto procentu formula

Saliktie procenti tiek aprēķināta pēc kopējās summas aprēķināšanas noteiktā laika periodā, pamatojoties uz procentu likmi un sākotnējo pamatsummu. Sākotnējai pamatsummai P, procentu likmei gadā r, laika periodam t gados, procentu salikšanas reižu biežumam gadā n, CI aprēķina formula ir šāda:

CI = P(1 + r/100) ⁿ – P

Iepriekš minētā formula salikto procentu aprēķināšanai ir pievienota tālāk esošajā attēla veidlapā:

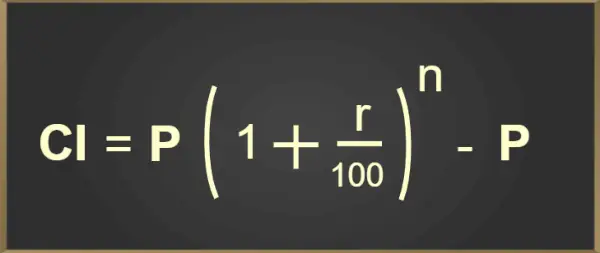
Salikto procentu formula

kur,

• P = galvenais
• r = procentu likme
• n = Reižu skaits, kad procenti tiek aprēķināti gadā
• t = laiks (gados)

Mēs varam uzrakstīt salikto procentu formulu šādi:

Saliktie procenti = A–P

kur,

• A = Kopējā naudas summa pēc sajaukšanas
• P = sākotnējā pamatsumma

Saliktie procenti = P(1 + r/n) ^nt -P

kur,

• P = sākotnējā pamatsumma
• r = gada procentu likme
• n = Procentu salikto reižu skaits
• t = gadu skaits

Saliktos procentus var aprēķināt katru gadu, pusgadu, ceturksni, mēnesi, dienu utt. atbilstoši prasībām.

Kā aprēķināt saliktos procentus?

Saliktie procenti ir procenti, kas maksāti gan par pamatsummu, gan uzkrātajiem procentiem. Katrā intervālā nopelnītie procenti tiek pievienoti sākotnējai pamatsummai, tādējādi pamatsumma turpina pieaugt.

Lai atrastu saliktos procentus, izmantojiet šādas metodes.

1. darbība: Norādīta piezīme, pamatsumma, likme un laika periods

2. darbība. Aprēķiniet summu, izmantojot formulu A = P(1 + r/100) ⁿ

3. darbība. Atrodiet saliktos procentus, izmantojot formulu CI = summa — pamatsumma

Ar regulāriem starplaikiem līdz šim uzkrātie procenti tiek saskaitīti ar esošo pamatsummu un pēc tam tiek aprēķināti procenti aprēķināts jaunajam pamatsummai . Jaunā pamatsumma ir vienāda ar Sākotnējās pamatsummas un līdz šim uzkrāto procentu summu.

Saliktie procenti = pamatsummas procenti + pamatsummas procenti (no otrā gada un uz priekšu)

Saliktie procenti tiek aprēķināti ar regulāriem intervāliem, piemēram, reizi gadā (gadā), pusgadā, reizi ceturksnī, mēnesī, utt.; Tas ir tāpat kā, atkārtoti ieguldot procentu ienākumus no ieguldījuma, nauda laika gaitā pieaug ātrāk! Tas ir tieši tas, ko saliktie procenti dara ar naudu. Bankas vai jebkura finanšu organizācija aprēķina summu, pamatojoties tikai uz saliktajiem procentiem.

Salikto procentu formula — atvasināšana

Salikto procentu formula ir spēcīgs instruments, ko izmanto finansēs, lai aprēķinātu nopelnītos vai samaksātos procentus par sākotnējo pamatsummu, kas ietver gan sākotnējo pamatsummu, gan iepriekšējos periodos uzkrātos procentus. Salikto procentu formulu nosaka:

kur,

• A ir ieguldījuma vai aizdevuma nākotnes vērtība, ieskaitot procentus
• P ir pamatsumma (sākotnējais ieguldījums vai aizdevuma summa)
• r ir gada procentu likme (kā decimāldaļa)
• n ir procentu salikšanas reižu skaits gadā
• t ir laiks, uz kuru nauda tiek ieguldīta vai aizņemta, gados

Vienkārša procentu formula

Vienkāršie procenti tiek aprēķināti tikai no pamatsummas. To var attēlot ar formulu ,

Salikto procentu formula ar nepārtrauktu salikšanu

Ja procentus saliek nepārtraukti (bezgalīgi daudzas reizes gadā), salikto procentu formula tiek iegūta, izmantojot nepārtrauktas salikšanas formulu:

kur,

• e ir Eilera skaitlis (aptuveni 2,71828)
• P ir pamatsumma
• r ir gada procentu likme
• t ir laiks gados

Vispārējā salikto procentu formula

Lai iegūtu vispārējo salikto procentu formulu, apsveriet salikto procentu aprēķināšanu n reizes gadā.

Ja P tiek salikts n reizes gadā ar gada procentu likmi r, procentus r dala ar n un piemēro n reizes gadā. Tātad pēc t gadiem formula kļūst:

kur,

• atspoguļo procentu likmi par salikšanas periodu.
• nt ir kopējais salikšanas periodu skaits t gadu laikā.

Šis formula parāda, kā sākotnējā pamatsumma laika gaitā pieaug, ja procenti tiek papildināti ar regulāriem intervāliem . Kad n tuvojas bezgalībai (t.i., nepārtraukta savienošana), formula tuvojas nepārtrauktās sajaukšanas formulai .

Kopsavilkumā, salikto procentu formula ir nepārtrauktas maisīšanas formulas rezultāts, kas pielāgota atsevišķiem sajaukšanas periodiem gadā. Tas ļauj aprēķināt ieguldījumu vai aizdevuma nākotnes vērtību, regulāri ņemot vērā saliktos procentus.

Pusgada salikto procentu formula

Lai ieguldītā pamatsumma ir P un procentu likme ir R % gadā, kas tiek salikts reizi pusgadā “t” gadiem

Kā tas tiek salikts reizi pusgadā, pamatsumma tiks mainīta 6 mēnešu beigās, un līdz tam nopelnītie procenti tiks pieskaitīti pamatsummai, un tad šī kļūst par jauno pamatsummu. Līdzīgi tiek aprēķināta galīgā summa.

Mēs zinām,

likme = R% gadā saliktā pusgada

likme = (R/2) %

laiks ir t gadi, mēs zinām, ka ir t gadi 2t pusgadu.

Tagad

A = P (1 + R/200) ^2t

CI = A–P

Ceturkšņa salikto procentu formula

Lai ieguldītā pamatsumma ir P un procentu likme ir R % gadā, kas tiek saskaitīta reizi ceturksnī t gadiem.

Kā to saliek reizi ceturksnī, pamatsumma tiks mainīta 3 mēnešu beigās, un līdz tam nopelnītie procenti tiks pieskaitīti pamatsummai, un tad tā kļūst par jauno pamatsummu. Līdzīgi tiek aprēķināta galīgā summa.

mēs zinām,

likme = R% gadā, salikts reizi ceturksnī

likme = (R/4)%

laiks ir t gadi, mēs zinām, ka ir t gadi 4t ceturtdaļas.

Tagad

A = P(1 + R/400) ^4t

CI = A–P

Pārbaudiet: Ceturkšņa salikto procentu formula

Mēneša salikto procentu formula

Ja procentus saliek katru mēnesi, salikšanas reižu skaits būs 12, un procenti katru mēnesi būs 1/12 no gada saliktajiem procentiem. Tādējādi ikmēneša salikto procentu formula tiek dota kā

A = P[1 + (R/1200)] ^12t

CI = A–P

Pārbaudiet: Mēneša salikto procentu formula

Ikdienas salikto procentu formula

Ja interese tiek papildināta katru dienu, tad.

Jaunā procentu likme būs R/365 %

n = 365

Tādējādi ikdienas salikto procentu formula tiek dota kā:

A = P[1 + (R/36500)] ^365t

CI = A–P

Periodiskās savienošanas ātruma formula

Kopējo summu, ieskaitot pamatsummu P un saliktos procentus CI, aprēķina:

A = P[1 + (r/n)] ^nt

kur,

• P = galvenais
• A = galīgā summa
• r = gada procentu likme
• n = Procentu salikšanas reižu skaits
• t = laiks (gados)

Tādējādi saliktie procenti ir:

CI = A–P

72. noteikums

72. noteikums ir formula, ko izmanto, lai novērtētu, cik gadu mūsu nauda tiek dubultota, ja to katru gadu saliek. Priekš piemērs , ja mūsu nauda tiek ieguldīta plkst r % salikt katru gadu, tad ir nepieciešami 72/r gadi, lai mūsu nauda tiktu dubultota.

Šis aprēķins ir noderīgs arī mūsu naudas uzpūstās vērtības aprēķināšanai, i., tas norāda, cik gadu laikā mūsu aktīva vērtība samazinās uz pusi, ja tā katru gadu tiek nolietota.

72 formulas noteikums

Šī formula tiek izmantota, lai aptuvenu gadu skaitu, kad mūsu ieguldījums dubultojas.

N = 72 / r

kur,

• N ir aptuvenais gadu skaits, kad mūsu nauda tiek dubultota
• r ir likme, pēc kuras mūsu nauda tiek apvienota katru gadu

72. noteikuma piemērs

Pieņemsim, ka Kabirs ir ieguldījis 10 00 000 rūpiju parāda fondā, kas nodrošina 8% atdevi. Atrodiet, pēc cik gadiem tā nauda tiek dubultota, ja to saliek katru gadu.

Izmantojot iepriekš minēto formulu: N = 72/8 = 9 gadi

Tādējādi ir vajadzīgi 9 gadi, lai Kabira nauda tiktu dubultota.

Saliktās procentu likmes vairākus gadus pēc kārtas

Ja mums ir vienāda summa un vienāda procentu likme. C.I. konkrētā gada C.I vienmēr ir vairāk nekā iepriekšējā gada C.I. (3. gada TI ir lielāks nekā 2. gada CI). Starpība starp CI jebkuriem diviem secīgiem gadiem ir viena gada procenti par iepriekšējā gada C.I.

3. gada C.I – 2. gada C.I = 2. gada C.I × r × 1/100

Starpība starp jebkuru divu secīgu gadu summām ir viena gada procenti no iepriekšējā gada summas.

3. gada summa – 2. gada summa = 2. gada summa × r × 1/100

Galvenie rezultāti

Kad mums ir vienāda summa un vienāda likme ,

C.I par n-to gadu = C.I par (n-1) gadu + procenti par vienu gadu par C.I par (n-1) gadu

Nepārtrauktas procentu formulas

Nepārtrauktās salikšanas formula tiek izmantota programmā Finance, lai aprēķinātu ieguldījuma galīgo vērtību, kas tiek nepārtraukti salikts dažādos laika periodos, un vērtība tiek pievienota laika gaitā. Nepārtrauktas maisīšanas formula ir dota kā

Galīgā vērtība = pašreizējā vērtība × e ^rt

kur,

• r ir procentu likme
• t ir laiks

Uzzināt vairāk, Nepārtrauktas savienošanas formula

Daži citi saliktas nozīmes lietojumi

Izaugsme: To galvenokārt izmanto izaugsmei, ja nozares ir saistītas.

Ražošana pēc n gadiem = sākotnējā ražošana × (1 + r/100) ⁿ

Nolietojums: Ja preces izmaksas katru gadu samazinās par r%, tad tās vērtība pēc n gadiem ir

Pašreizējā vērtība × (1 + r/100) ⁿ

Iedzīvotāju problēmas: kad pilsētas, pilsētas vai ciema iedzīvotāju skaits pieaug ar noteiktu ātrumu gadā.

Iedzīvotāju skaits pēc n gadiem = pašreizējais iedzīvotāju skaits × (1 + r/100) ⁿ

Atšķirība starp saliktajiem procentiem un vienkāršiem procentiem

Par atšķirību starp saliktajiem procentiem un vienkāršiem procentiem var uzzināt tālāk šajā rakstā

Saliktie procenti pret vienkāršiem procentiem
Saliktie procenti (CI)	Vienkāršā procentu likme (SI)
CI ir procenti, kas tiek aprēķināti gan no pamatsummas, gan iepriekš nopelnītajiem procentiem.	SI ir procenti, kas tiek aprēķināti tikai no pamatsummas.
Tam pašam principam, likmei un laika periodam CI> JĀ	Tam pašam principam, likmei un laika periodam JĀ
CI formula ir A = P(1 + R/100) T CI = A–P	Formula SI ir IF = (P × R × T) / 100

Salikto procentu piemēri

Daži salikto procentu formulu piemēri ir:

1. piemērs. Atrodiet saliktos procentus, ja pamatsumma = 6000 Rs, likme = 10% gadā un laiks = 2 gadi.

Risinājums:

Procenti par pirmo gadu = (6000 × 10 × 1)/100 = 600

Summa pirmā gada beigās = 6000 + 600 = 6600

Procenti par otro gadu = (6600 × 10 × 1) / 100 = 660

Summa otrā gada beigās = 6600 + 660 = 7260

Saliktie procenti = 7260–6000 = 1260

2. piemērs. Kādi būs saliktie procenti Rs 8000 pēc diviem gadiem, ja procentu likme ir 2% gadā?

Risinājums:

Ņemot vērā,

• Galvenā P = 8000
• Likme r = 2%
• Laiks = 2 gadi

pēc formulas

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100) ² = 8000 (102/100) ²

A = 8323

Saliktie procenti = A – P = 8323 – 8000 = 323 Rs

3. piemērs: Hari noguldīja Rs. 4000 ar finanšu kompāniju uz 2 gadiem ar procentiem 5% gadā. Kādi ir saliktie procenti, ko Rohits saņem pēc 2 gadiem?

Risinājums:

Ņemot vērā,

• Galvenā P = 4000
• Likme r = 5%
• Laiks = 2 gadi

Pēc formulas,

A = P (1 + R/100) ⁿ

A= 4000 (1 + 5/100) ²

A= 4000 (105/100) ²

A = 4410

Saliktie procenti = A – P = 4410 – 4000 = 410

4. piemērs. Atrodiet saliktos procentus par Rs. 2000 ar likmi 4 % gadā 1,5 gadus. Kad procenti tiek pieskaitīti reizi pusgadā?

Risinājums:

Ņemot vērā,

• Galvenā p = 2000
• Likme r = 4%
• Laiks = 1,5 (t.i., 3 pusgadi)

pēc formulas,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Saliktie procenti = A – P = 2122 – 2000 = 122

5. piemērs. Kādi ir saliktie procenti par 10 000 par vienu gadu ar likmi 20% gadā, ja procentus saliek reizi ceturksnī?

Risinājums:

Ņemot vērā,

• Pamatsumma P = 10 000 Rs
• Likme R = 12% (12/4 = 3% ceturksnī gadā)
• Laiks = 1 gads (1 × 4 = 4 ceturkšņi)

Pēc formulas,

A = P (1 + R/100) ⁿ

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

A = 11255

Saliktie procenti = A – P = 11255 – 10000 = 1255

6. piemērs. Atrodiet saliktos procentus ar likmi 5% gadā uz 2 gadiem no pamatsummas, kas 2 gados ar likmi 5% gadā, ņemot vērā Rs. 400 kā vienkārši procenti.

Risinājums:

Ņemot vērā,

• Vienkāršā procentu likme, ja = 400
• Likme R = 5%
• Laiks T = 2 gadi

Pēc formulas,

Vienkāršie procenti = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 saliktā procentu likme = 5%

P = 40000/10 = 4000 Rs

Laiks = 2 gadi

Pēc formulas,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Saliktie procenti = A – P = 4410 – 4000 = 410

7. piemērs. Atrodiet saliktos procentus par Rs 30000 ar 7% procentiem, ko katru gadu saliek divus gadus.

Risinājums:

• Pamatsumma P = 30 000 Rs
• Likme R = 7%
• Laiks = 2 gadi

Pēc formulas,

A = P (1 + R/100) ⁿ

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

A = 34347

Saliktie procenti = A – P = 34347 – 30000 = 4347

Saistītie lasījumi:

• Dienas saliktie procenti
• Mēneša saliktie procenti
• 8. klases salikto procentu risinājums
• Saliktās intereses — spēju jautājumi un atbildes
• Vienkārša interese

Saliktās intereses — prakses jautājumi

Dažādi prakses jautājumi par saliktajām procentu likmēm ir:

Q1. Atrodiet summu, kas jāmaksā pēc 3 gadiem, ja tiek aizdots 10 000 ar likmi 4% gadā.

Q2. Atrodiet procentus, kas ir jāmaksā pēc 1,5 gadiem, ja tiek aizdots 2500 summa ar likmi 6%, pieskaitot to pusgadā.

Q3. Aprēķiniet saliktos procentus par aizdoto summu 9000 ar likmi 5% reizi ceturksnī 15 mēnešus.

Q4. Aprēķiniet saliktos procentus par aizdoto summu 20 000 ar likmi 12% uz 3 mēnešiem, saliekot katru mēnesi

Secinājums par saliktajiem procentiem

Saliktie procenti ir a spēcīga finanšu koncepcija, kas ļauj investīcijām vai aizdevumiem laika gaitā pieaugt vai uzkrāties. Atšķirībā no vienkāršie procenti, kas aprēķina procentus tikai no sākotnējās pamatsummas, saliktie procenti ņem vērā procentus, kas nopelnīti gan par sākotnējo pamatsummu, gan jebkuriem uzkrātajiem procentiem no iepriekšējiem periodiem.

Saliktās procentu likmes — FAQ

Kāda salikto interešu nozīme?

Saliktie procenti ir procenti, kas aprēķināti par pamatsummu, kā arī iepriekš nopelnītie procenti noteiktā laika periodā

Kā aprēķināt saliktos procentus?

Lai aprēķinātu saliktos procentus, vispirms tiek aprēķināta galīgā summa, pēc tam tā tiek atņemta no pamatsummas, lai iegūtu galīgos saliktos procentus. Summu aprēķina pēc formulas,

A = P(1 + R/100) ^t

CI = A–P

Vai ieguldītājiem saliktie procenti ir labāki par vienkāršiem procentiem?

Jā, ieguldītājiem saliktie procenti ir daudz labāki nekā vienkāršie procenti.

Kas ir salikto procentu formula, ja to saliek katru dienu?

Pieņemsim, ka dotā pamatsumma ir P, likme ir R un laika intervāls ir T gadi, tad salikto procentu formula, ja to saliek katru dienu, ir:

A = P(1 + R/365) ^{{365 × T}}

Kāda ir atšķirība starp CI un SI?

Galvenā atšķirība starp CI un SI ir SI ir procenti, kas tiek iekasēti no pamatsummas, savukārt CI ir procenti, kas tiek iekasēti no pamatsummas, kā arī no procentiem, kas uzkrāti par pamatsummu