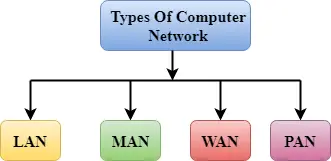
Attiecību sastāvs

Lai A, B un C ir kopas, un lai R ir attiecība no A līdz B un lai S ir attiecība no B līdz C. Tas ir, R ir A × B apakškopa un S ir B × apakškopa. C. Tad R un S rada attiecību no A līdz C, ko apzīmē ar R◦S un definē ar:
a (R◦S)c if for some b ∈ B we have aRb and bSc. That is, R ◦ S = there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S
Sakarība R◦S ir zināma R un S sastāvs; to dažreiz apzīmē vienkārši ar RS.
Pieņemsim, ka R ir kopas A relācija, tas ir, R ir kopas A attiecība pret sevi. Tad vienmēr tiek attēlots R◦R, R sastāvs ar sevi. Arī R◦R dažreiz apzīmē ar R 2 . Līdzīgi R 3 = R 2 ◦R = R◦R◦R un tā tālāk. Tādējādi R n ir definēts visiem pozitīvajiem n.
1. piemērs: Pieņemsim, ka X = {4, 5, 6}, Y = {a, b, c} un Z = {l, m, n}. Apsveriet attiecību R 1 no X uz Y un R 2 no Y līdz Z.
R<sub>1</sub> = {(4, a), (4, b), (5, c), (6, a), (6, c)} R<sub>2</sub> = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)} 
Atrodiet attiecības sastāvu (i) R 1 R 2 (ii) R 1 R 1 -1
Risinājums:
(i) sastāva attiecība R 1 R 2 kā parādīts attēlā:

R 1 R 2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
(ii) sastāva attiecība R 1 R 1 -1 kā parādīts attēlā:

R 1 R 1 -1 = {(4, 4), (5, 5), (5, 6), (6, 4), (6, 5), (4, 6), (6, 6)}
Attiecību un matricu sastāvs
Ir vēl viens veids, kā atrast R◦S. Ļaujiet M R un M S apzīmē attiecīgi relāciju R un S matricas atveidojumus. Tad
Piemērs
Let P = {2, 3, 4, 5}. Consider the relation R and S on P defined by R = {(2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 3)} S = {(2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 3), (4, 5), (5, 2), (5, 5)}. Find the matrices of the above relations. Use matrices to find the following composition of the relation R and S. (i)RoS (ii)RoR (iii)SoR Risinājums: Attiecības R un S matricas ir parādītas attēlā:

(i) Lai iegūtu attiecības R un S sastāvu. Vispirms reiziniet M R ar M S lai iegūtu matricu M R x M S kā parādīts attēlā:
Ieraksti, kas nav nulles matricā M R x M S stāsta RoS saistītos elementus. Tātad,

Līdz ar to attiecības R un S sastāvs R o S ir
R o S = {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (4, 2), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}. (ii) Vispirms reiziniet matricu M R pats par sevi, kā parādīts attēlā

Līdz ar to attiecības R un S sastāvs R o R ir
R o R = {(2, 2), (3, 2), (3, 3), (3, 4), (4, 2), (4, 5), (5, 2), (5, 3), (5, 5)} (iii) Reiziniet matricu M S ar M R lai iegūtu matricu M S x M R kā parādīts attēlā:

Ieraksti, kas atšķiras no nulles matricā M S x M R stāsta par elementiem, kas saistīti ar S o R.
Līdz ar to attiecības S un R sastāvs S o R ir
S o R = {(2, 4) , (2, 5), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}.