Binārā uz pelēko kodu konvertēšana

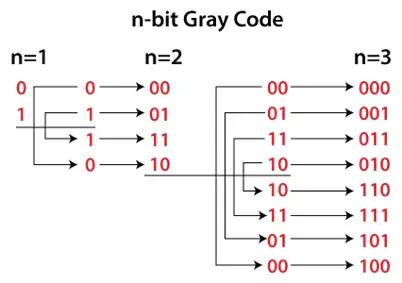
Binārā uz pelēko kodu pārveidotājs ir loģiska shēma, ko izmanto, lai bināro kodu pārvērstu līdzvērtīgā pelēkajā kodā. Novietojot MSB 1 zem ass un MSB 1 virs ass un atspoguļojot (n-1) bitu kodu ap asi pēc 2 n-1 rindas, mēs varam iegūt n-bitu pelēko kodu.
4 bitu binārā uz pelēko kodu konvertēšanas tabula ir šāda:
| Decimālskaitlis | 4 bitu binārais kods | 4 bitu pelēkais kods |
|---|---|---|
| ABCD | G 1 G 2 G 3 G 4 | |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001. gads | 1101 |
| 10 | 1010. gads | 1111 |
| vienpadsmit | 1011. gads | 1110 |
| 12 | 1100 | 1010. gads |
| 13 | 1101 | 1011. gads |
| 14 | 1110 | 1001. gads |
| piecpadsmit | 1111 | 1000 |
4 bitu pelēkajā kodā 3 bitu kods tiek atspoguļots pret asi, kas novilkta pēc 2. 4-1 -1 th =8 th rinda.

Kā konvertēt bināro kodu uz pelēko kodu
- Pelēkajā kodā MSB vienmēr būs tāds pats kā dotā binārā skaitļa 1. bits.
- Lai veiktu 2 nd pelēkā koda bitu, mēs veicam ekskluzīvo vai (XOR) 1. un 2 nd binārā skaitļa bits. Tas nozīmē, ka, ja abi biti ir atšķirīgi, rezultāts būs cits, rezultāts būs 0.
- Lai iegūtu 3 rd pelēkā koda bitu, mums ir jāveic ekskluzīvais vai (XOR) 2 nd un 3 rd binārā skaitļa bits. Process paliek tāds pats 4 th mazliet Grey koda. Ņemsim piemēru, lai saprastu šīs darbības.
Piemērs
Pieņemsim, ka mums ir binārs skaitlis 01101, kuru mēs vēlamies pārvērst pelēkajā kodā. Lai veiktu šo konvertēšanu, ir jāveic šādas darbības:
- Kā mēs zinām, ka 1 st Grey koda bits ir tāds pats kā binārā skaitļa MSB. Mūsu piemērā MSB ir 0, tātad MSB vai 1 st pelēkā koda bits ir 0.
- Tālāk mēs veicam 1. un otrā binārā skaitļa XOR darbību. 1 st bits ir 0, bet 2 nd bits ir 1. Abi biti ir atšķirīgi, tāpēc 2 nd Grey koda bits ir 1.
- Tagad mēs veicam 2. XOR nd bits un 3 rd binārā skaitļa bits. 2 nd bits ir 1 un 3 rd bits arī ir 1. Šie biti ir vienādi, tāpēc 3 rd Grey koda bits ir 0.
- Vēlreiz veiciet XOR darbību ar 3 rd un 4 th binārā skaitļa bits. 3 rd bits ir 1 un 4 th bits ir 0. Tā kā tie ir atšķirīgi, 4 th Grey koda bits ir 1.
- Visbeidzot, veiciet 4. XOR th bits un 5 th binārā skaitļa bits. 4 th bits ir 0, bet 5 th bits ir 1. Abi biti ir atšķirīgi, tāpēc 5 th Grey koda bits ir 1.
- Binārā skaitļa 01101 pelēkais kods ir 01011.

Pelēkā koda konvertēšana uz bināro kodu
Pelēkā binārā koda pārveidotājs ir loģiska shēma, ko izmanto, lai pelēko kodu pārvērstu līdzvērtīgā binārajā kodā. Ir šāda shēma, ko izmanto, lai pārvērstu Grey kodu binārā skaitļā.

Tāpat kā binārā uz pelēko kodu konvertēšana; tas ir arī ļoti vienkāršs process. Lai Grey kodu pārvērstu binārā, ir jāveic šādas darbības.
- Tāpat kā no bināra uz pelēku, no pelēka uz bināru, 1 st binārā skaitļa bits ir līdzīgs Grey koda MSB.
- 2 nd binārā skaitļa bits ir tāds pats kā 1 st binārā skaitļa bits, kad 2 nd Grey koda bits ir 0; pretējā gadījumā 2 nd bits ir mainīts bits no 1 st binārā skaitļa bits. Tas nozīmē, ja 1 st binārais bits ir 1, tad 2 nd bits ir 0, un, ja tas ir 0, tad 2 nd mazliet būt 1.
- 2 nd solis turpinās visiem binārā skaitļa bitiem.

Pelēkā koda binārās konvertēšanas piemērs
Pieņemsim, ka mums ir pelēkais kods 01011, kuru mēs vēlamies pārveidot par bināru skaitli. Lai veiktu reklāmguvumu, ir jāveic šādas darbības:
- Binārā skaitļa 1. bits ir tāds pats kā Grey koda MSB. Grey koda MSB ir 0, tātad binārā skaitļa MSB ir 0.
- Tagad par 2 nd bitu, mēs pārbaudām 2 nd mazliet Grey koda. 2 nd Grey koda bits ir 1, tātad 2 nd binārā skaitļa bits ir tāds, kas ir mainīts skaitlis 1 st
- Nākamais Grey koda bits ir 0; 3 rd bits ir tāds pats kā 2 nd Grey koda bits, t.i., 1.
- 4 th Grey koda bits ir 1; 4 th binārā skaitļa bits ir 0, kas ir mainīts skaitlis no 3 rd
- 5 th Grey koda bits ir 1; 5 th binārā skaitļa bits ir 1; tas ir izmainītais skaitlis no 4 th binārā skaitļa bits.
- Tātad pelēkā koda 01011 binārais numurs ir 01101.
4 bitu pelēkā koda biti tiek uzskatīti par G 4 G 3 G 2 G 1 . Tagad no reklāmguvumu tabulas

The Karnaugh kartes (K-kartes) G 4 , G 3 , G 2, un G 1 ir šādi: