ALGORITHME DE LUHN

L'algorithme de Luhn, également connu sous le nom de module 10 ou vers 10 algorithme, est une formule de somme de contrôle simple utilisée pour valider une variété de numéros d'identification, tels que les numéros de carte de crédit, les numéros IMEI, les numéros d'assurance sociale canadienne. La formule LUHN a été créée à la fin des années 1960 par un groupe de mathématiciens. Peu de temps après, les sociétés émettrices de cartes de crédit l’ont adopté. L’algorithme étant dans le domaine public, il peut être utilisé par n’importe qui. La plupart des cartes de crédit et de nombreux numéros d'identification gouvernementaux utilisent l'algorithme comme méthode simple pour distinguer les numéros valides des numéros mal saisis ou incorrects. Il a été conçu pour protéger contre les erreurs accidentelles et non contre les attaques malveillantes.

Étapes impliquées dans l'algorithme de Luhn

Comprenons l'algorithme avec un exemple :
Prenons l'exemple d'un numéro de compte 79927398713 .

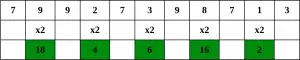
Étape 1 – En partant du chiffre le plus à droite, doublez la valeur d’un chiffre sur deux,

Étape 2 – Si le doublement d'un nombre donne un nombre à deux chiffres, c'est-à-dire supérieur à 9 (par exemple, 6 × 2 = 12), alors additionnez les chiffres du produit (par exemple, 12 : 1 + 2 = 3, 15 : 1 + 5 = 6), pour obtenir un numéro à un chiffre.

Étape 3 – Maintenant, faites la somme de tous les chiffres.

Étape 4 – Si le total modulo 10 est égal à 0 (si le total se termine par zéro) alors le nombre est valable selon la formule de Luhn ; sinon, ce n'est pas valide.

Puisque la somme est de 70 qui est un multiple de 10, le numéro de compte est peut-être valide.

L'idée est simple ; nous traversons depuis la fin. Pour un chiffre sur deux, nous le doublons avant de l’ajouter. On additionne deux chiffres du nombre obtenu après doublement.

Mise en œuvre:

C++

// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(> const> string& cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum = 0, isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0 ; je--) {> > int> d = cardNo[i] -> '0'> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits after> > // doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> > string cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > printf> (> 'This is a valid card'> );> > else> > printf> (> 'This is not a valid card'> );> > return> 0;> }>

Java

// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum => 0> ;> > boolean> isSecond => false> ;> > for> (> int> i = nDigits -> 1> ; i>=> 0> ; i--)> > {> > int> d = cardNo.charAt(i) -> '0'> ;> > if> (isSecond ==> true> )> > d = d *> 2> ;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d /> 10> ;> > nSum += d %> 10> ;> > isSecond = !isSecond;> > }> > return> (nSum %> 10> ==> 0> );> }> > // Driver code> > static> public> void> main (String[] args)> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > System.out.println(> 'This is a valid card'> );> > else> > System.out.println(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

Python3

# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > > nDigits> => len> (cardNo)> > nSum> => 0> > isSecond> => False> > > for> i> in> range> (nDigits> -> 1> ,> -> 1> ,> -> 1> ):> > d> => ord> (cardNo[i])> -> ord> (> '0'> )> > > if> (isSecond> => => True> ):> > d> => d> *> 2> > > # We add two digits to handle> > # cases that make two digits after> > # doubling> > nSum> +> => d> /> /> 10> > nSum> +> => d> %> 10> > > isSecond> => not> isSecond> > > if> (nSum> %> 10> => => 0> ):> > return> True> > else> :> > return> False> # Driver code> if> __name__> => => '__main__'> :> > > cardNo> => '79927398713'> > > if> (checkLuhn(cardNo)):> > print> (> 'This is a valid card'> )> > else> :> > print> (> 'This is not a valid card'> )> # This code is contributed by rutvik_56>

C#

// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.Length;> > int> nSum = 0;> > bool> isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0 ; je--)> > {> > int> d = cardNo[i] -> '0'> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> > // Driver code> > static> public> void> Main()> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > Console.WriteLine(> 'This is a valid card'> );> > else> > Console.WriteLine(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

Javascript

> > // Javascript program to implement Luhn algorithm> > > // Returns true if given> > // card number is valid> > function> checkLuhn(cardNo)> > {> > let nDigits = cardNo.length;> > let nSum = 0;> > let isSecond => false> ;> > for> (let i = nDigits - 1; i>= 0 ; je--)> > {> > let d = cardNo[i].charCodeAt() -> '0'> .charCodeAt();> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += parseInt(d / 10, 10);> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> > }> > > let cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > document.write(> 'This is a valid card'> );> > else> > document.write(> 'This is not a valid card'> );> > >

Sortir