Spausdinami visi N-Queen problemos sprendimai
Duotas sveikasis skaičius n užduotis yra surasti viską skirtingus sprendimus prie n-queens problema kur n karalienės dedamos ant an n * n šachmatų lenta taip, kad dvi karalienės negalėtų užpulti viena kitos.
Pastaba: Kiekvienas sprendimas yra unikali konfigūracija n karalienės vaizduojamos kaip permutacija [123....n] . Numeris adresu i th padėtis rodo karalienės eilutę i th stulpelyje. Pavyzdžiui [3142] rodo vieną tokį išdėstymą.
Pavyzdys:
Įvestis: n = 4
Išvestis: [2 4 1 3] [3 1 4 2]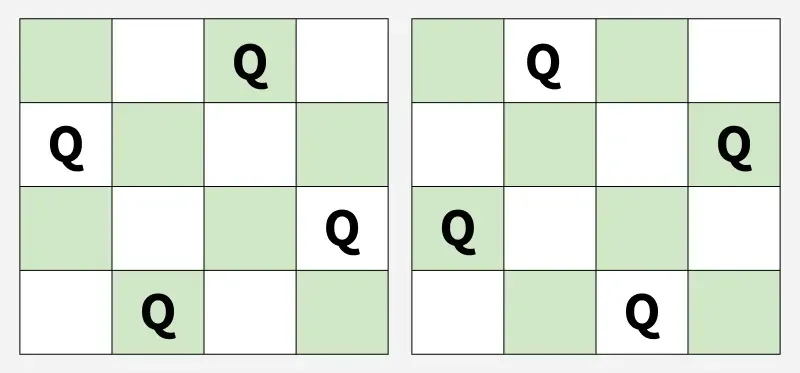
Paaiškinimas: Tai yra 2 galimi sprendimai.Įvestis: n = 2
Išvestis: []
Paaiškinimas: Nėra sprendimo, nes karalienės gali pulti viena kitą visomis įmanomomis konfigūracijomis.
Turinio lentelė
- [Naivus požiūris] Generuojant visas permutacijas naudojant rekursiją
- [Numatomas metodas] Atšaukimo naudojimas su genėjimu
- [Alternatyvus metodas] Grįžimas naudojant bitų maskavimą
[Naivus požiūris] – Rekursijos naudojimas – O(n! * n) laikas ir O(n) erdvė
Paprasta idėja išspręsti N-Queens problema yra sukurti visas įmanomas permutacijas [1 2 3 ... n] tada patikrinkite, ar ji atitinka galiojančią N-Queens konfigūraciją. Kadangi kiekviena karalienė turi būti skirtingoje eilutėje ir stulpelyje naudojant permutacijas automatiškai rūpinasi tomis taisyklėmis. Bet vis tiek turime patikrinti, ar ant jo nėra dviejų karalienių ta pati įstrižainė.
Žemiau pateikiama įgyvendinimas:
C++ //C++ program to find all solution of N queen problem //using recursion #include #include #include using namespace std ; // Function to check if the current placement is safe bool isSafe ( vector < int >& board int currRow int currCol ) { // Check all previously placed queens for ( int i = 0 ; i < board . size (); ++ i ) { int placedRow = board [ i ]; // Columns are 1-based int placedCol = i + 1 ; // Check if the queen is on the same diagonal if ( abs ( placedRow - currRow ) == abs ( placedCol - currCol )) { return false ; // Not safe } } // Safe to place the queen return true ; } // Recursive function to generate all possible permutations void nQueenUtil ( int col int n vector < int >& board vector < vector < int >>& res vector < bool >& visited ) { // If all queens are placed add into res if ( col > n ) { res . push_back ( board ); return ; } // Try placing a queen in each row // of the current column for ( int row = 1 ; row <= n ; ++ row ) { // Check if the row is already used if ( ! visited [ row ]) { // Check if it's safe to place the queen if ( isSafe ( board row col )) { // Mark the row as used visited [ row ] = true ; // Place the queen board . push_back ( row ); // Recur to place the next queen nQueenUtil ( col + 1 n board res visited ); // Backtrack: remove the queen board . pop_back (); // Unmark row visited [ row ] = false ; } } } } // Main function to find all distinct // res to the n-queens puzzle vector < vector < int >> nQueen ( int n ) { vector < vector < int >> res ; // Current board configuration vector < int > board ; // Track used rows vector < bool > visited ( n + 1 false ); // Start solving from the first column nQueenUtil ( 1 n board res visited ); return res ; } int main () { int n = 4 ; vector < vector < int >> res = nQueen ( n ); for ( int i = 0 ; i < res . size (); i ++ ) { cout < < '[' ; for ( int j = 0 ; j < n ; ++ j ) { cout < < res [ i ][ j ]; if ( j != n - 1 ) cout < < ' ' ; } cout < < '] n ' ; } return 0 ; }
Java //Java program to find all solution of N queen problem //using recursion import java.util.ArrayList ; class GfG { // Check if placement is safe static boolean isSafe ( ArrayList < Integer > board int currRow int currCol ) { for ( int i = 0 ; i < board . size (); i ++ ) { int placedRow = board . get ( i ); int placedCol = i + 1 ; // Check diagonals if ( Math . abs ( placedRow - currRow ) == Math . abs ( placedCol - currCol )) { return false ; // Not safe } } return true ; // Safe to place } // Recursive utility to solve static void nQueenUtil ( int col int n ArrayList < Integer > board ArrayList < ArrayList < Integer >> res boolean [] visited ) { // If all queens placed add to res if ( col > n ) { res . add ( new ArrayList <> ( board )); return ; } // Try each row in column for ( int row = 1 ; row <= n ; row ++ ) { // If row not used if ( ! visited [ row ] ) { // Check safety if ( isSafe ( board row col )) { // Mark row visited [ row ] = true ; // Place queen board . add ( row ); // Recur for next column nQueenUtil ( col + 1 n board res visited ); // Backtrack board . remove ( board . size () - 1 ); visited [ row ] = false ; } } } } // Function to solve N-Queen static ArrayList < ArrayList < Integer >> nQueen ( int n ) { ArrayList < ArrayList < Integer >> res = new ArrayList <> (); ArrayList < Integer > board = new ArrayList <> (); boolean [] visited = new boolean [ n + 1 ] ; nQueenUtil ( 1 n board res visited ); return res ; } public static void main ( String [] args ) { int n = 4 ; ArrayList < ArrayList < Integer >> res = nQueen ( n ); for ( ArrayList < Integer > row : res ) { System . out . print ( '[' ); for ( int i = 0 ; i < row . size (); i ++ ) { System . out . print ( row . get ( i )); if ( i != row . size () - 1 ) System . out . print ( ' ' ); } System . out . println ( ']' ); } } }
Python #Python program to find all solution of N queen problem #using recursion # Function to check if placement is safe def isSafe ( board currRow currCol ): for i in range ( len ( board )): placedRow = board [ i ] placedCol = i + 1 # Check diagonals if abs ( placedRow - currRow ) == abs ( placedCol - currCol ): return False # Not safe return True # Safe to place # Recursive utility to solve N-Queens def nQueenUtil ( col n board res visited ): # If all queens placed add to res if col > n : res . append ( board . copy ()) return # Try each row in column for row in range ( 1 n + 1 ): # If row not used if not visited [ row ]: # Check safety if isSafe ( board row col ): # Mark row visited [ row ] = True # Place queen board . append ( row ) # Recur for next column nQueenUtil ( col + 1 n board res visited ) # Backtrack board . pop () visited [ row ] = False # Main N-Queen solver def nQueen ( n ): res = [] board = [] visited = [ False ] * ( n + 1 ) nQueenUtil ( 1 n board res visited ) return res if __name__ == '__main__' : n = 4 res = nQueen ( n ) for row in res : print ( row )
C# //C# program to find all solution of N queen problem //using recursion using System ; using System.Collections.Generic ; class GfG { // Check if placement is safe static bool isSafe ( List < int > board int currRow int currCol ){ for ( int i = 0 ; i < board . Count ; i ++ ) { int placedRow = board [ i ]; int placedCol = i + 1 ; // Check diagonals if ( Math . Abs ( placedRow - currRow ) == Math . Abs ( placedCol - currCol )) { return false ; // Not safe } } return true ; // Safe to place } // Recursive utility to solve static void nQueenUtil ( int col int n List < int > board List < List < int > > res bool [] visited ){ // If all queens placed add to res if ( col > n ) { res . Add ( new List < int > ( board )); return ; } // Try each row in column for ( int row = 1 ; row <= n ; row ++ ) { // If row not used if ( ! visited [ row ]) { // Check safety if ( isSafe ( board row col )) { // Mark row visited [ row ] = true ; // Place queen board . Add ( row ); // Recur for next column nQueenUtil ( col + 1 n board res visited ); // Backtrack board . RemoveAt ( board . Count - 1 ); visited [ row ] = false ; } } } } // Main N-Queen solver static List < List < int >> nQueen ( int n ){ List < List < int > > res = new List < List < int > > (); List < int > board = new List < int > (); bool [] visited = new bool [ n + 1 ]; nQueenUtil ( 1 n board res visited ); return res ; } static void Main ( string [] args ) { int n = 4 ; List < List < int >> res = nQueen ( n ); foreach ( var temp in res ) { Console . WriteLine ( '[' + String . Join ( ' ' temp ) + ']' ); } } }
JavaScript //JavaScript program to find all solution of N queen problem //using recursion // Function to check if placement is safe function isSafe ( board currRow currCol ){ for ( let i = 0 ; i < board . length ; i ++ ) { let placedRow = board [ i ]; let placedCol = i + 1 ; // Check diagonals if ( Math . abs ( placedRow - currRow ) === Math . abs ( placedCol - currCol )) { return false ; // Not safe } } return true ; // Safe to place } // Recursive utility to solve N-Queens function nQueenUtil ( col n board res visited ){ // If all queens placed add to res if ( col > n ) { res . push ([... board ]); return ; } // Try each row in column for ( let row = 1 ; row <= n ; row ++ ) { // If row not used if ( ! visited [ row ]) { // Check safety if ( isSafe ( board row col )) { // Mark row visited [ row ] = true ; // Place queen board . push ( row ); // Recur for next column nQueenUtil ( col + 1 n board res visited ); // Backtrack board . pop (); visited [ row ] = false ; } } } } // Main N-Queen solver function nQueen ( n ){ let res = []; let board = []; let visited = Array ( n + 1 ). fill ( false ); nQueenUtil ( 1 n board res visited ); return res ; } // Driver code let n = 4 ; let res = nQueen ( n ); res . forEach ( row => console . log ( row ));
Išvestis
[2 4 1 3] [3 1 4 2]
Laiko sudėtingumas: O(n!*n) n! už visų generavimą permutacijas ir O(n) kiekvienos permutacijos patvirtinimui.
Pagalbinė erdvė: O(n)
[Numatomas metodas] – Atgalinio judėjimo naudojimas su genėjimu – O(n!) laikas ir O(n) erdvė
Norėdami optimizuoti aukščiau pateiktą metodą, galime naudoti atsitraukimas su genėjimu . Užuot generavę visas įmanomas permutacijas, sprendimą kuriame laipsniškai, tai darydami galime užtikrinti, kad kiekviename žingsnyje dalinis sprendimas išliktų galiojantis. Jei kiltų konfliktas, mes nedelsdami atsitrauksime, tai padės vengiant nereikalingas skaičiavimai .
Žingsnis po žingsnio įgyvendinimas :
- Pradėkite nuo pirmojo stulpelio ir pabandykite įdėti karalienę kiekvienoje eilutėje.
- Laikykite masyvus, kad galėtumėte stebėti, kurie eilučių jau yra užimti. Panašiai ir sekimui majoras ir nedidelės įstrižainės jau yra užimti.
- Jei karalienė išdėstymas konfliktai su esamomis karalienėmis praleisti kad eilė ir atsitraukti karalienė pabandyti kitą galima eilutė (genėti ir grįžti atgal konflikto metu).
// C++ program to find all solution of N queen problem by // using backtracking and pruning #include #include #include using namespace std ; // Utility function for solving the N-Queens // problem using backtracking. void nQueenUtil ( int j int n vector < int > & board vector < bool > & rows vector < bool > & diag1 vector < bool > & diag2 vector < vector < int >> & res ) { if ( j > n ) { // A solution is found res . push_back ( board ); return ; } for ( int i = 1 ; i <= n ; ++ i ) { if ( ! rows [ i ] && ! diag1 [ i + j ] && ! diag2 [ i - j + n ]) { // Place queen rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = true ; board . push_back ( i ); // Recurse to the next column nQueenUtil ( j + 1 n board rows diag1 diag2 res ); // Remove queen (backtrack) board . pop_back (); rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = false ; } } } // Solves the N-Queens problem and returns // all valid configurations. vector < vector < int >> nQueen ( int n ) { vector < vector < int >> res ; vector < int > board ; // Rows occupied vector < bool > rows ( n + 1 false ); // Major diagonals (row + j) and Minor diagonals (row - col + n) vector < bool > diag1 ( 2 * n + 1 false ); vector < bool > diag2 ( 2 * n + 1 false ); // Start solving from the first column nQueenUtil ( 1 n board rows diag1 diag2 res ); return res ; } int main () { int n = 4 ; vector < vector < int >> res = nQueen ( n ); for ( int i = 0 ; i < res . size (); i ++ ) { cout < < '[' ; for ( int j = 0 ; j < n ; ++ j ) { cout < < res [ i ][ j ]; if ( j != n - 1 ) cout < < ' ' ; } cout < < '] n ' ; } return 0 ; }
Java // Java program to find all solutions of the N-Queens problem // using backtracking and pruning import java.util.ArrayList ; import java.util.List ; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil ( int j int n ArrayList < Integer > board boolean [] rows boolean [] diag1 boolean [] diag2 ArrayList < ArrayList < Integer >> res ) { if ( j > n ) { // A solution is found res . add ( new ArrayList <> ( board )); return ; } for ( int i = 1 ; i <= n ; ++ i ) { if ( ! rows [ i ] && ! diag1 [ i + j ] && ! diag2 [ i - j + n ] ) { // Place queen rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = true ; board . add ( i ); // Recurse to the next column nQueenUtil ( j + 1 n board rows diag1 diag2 res ); // Remove queen (backtrack) board . remove ( board . size () - 1 ); rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = false ; } } } // Solves the N-Queens problem and returns // all valid configurations. static ArrayList < ArrayList < Integer >> nQueen ( int n ) { ArrayList < ArrayList < Integer >> res = new ArrayList <> (); ArrayList < Integer > board = new ArrayList <> (); // Rows occupied boolean [] rows = new boolean [ n + 1 ] ; // Major diagonals (row + j) and Minor diagonals (row - col + n) boolean [] diag1 = new boolean [ 2 * n + 1 ] ; boolean [] diag2 = new boolean [ 2 * n + 1 ] ; // Start solving from the first column nQueenUtil ( 1 n board rows diag1 diag2 res ); return res ; } public static void main ( String [] args ) { int n = 4 ; ArrayList < ArrayList < Integer >> res = nQueen ( n ); for ( ArrayList < Integer > solution : res ) { System . out . print ( '[' ); for ( int i = 0 ; i < solution . size (); i ++ ) { System . out . print ( solution . get ( i )); if ( i != solution . size () - 1 ) { System . out . print ( ' ' ); } } System . out . println ( ']' ); } } }
Python # Python program to find all solutions of the N-Queens problem # using backtracking and pruning def nQueenUtil ( j n board rows diag1 diag2 res ): if j > n : # A solution is found res . append ( board [:]) return for i in range ( 1 n + 1 ): if not rows [ i ] and not diag1 [ i + j ] and not diag2 [ i - j + n ]: # Place queen rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = True board . append ( i ) # Recurse to the next column nQueenUtil ( j + 1 n board rows diag1 diag2 res ) # Remove queen (backtrack) board . pop () rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = False def nQueen ( n ): res = [] board = [] # Rows occupied rows = [ False ] * ( n + 1 ) # Major diagonals (row + j) and Minor diagonals (row - col + n) diag1 = [ False ] * ( 2 * n + 1 ) diag2 = [ False ] * ( 2 * n + 1 ) # Start solving from the first column nQueenUtil ( 1 n board rows diag1 diag2 res ) return res if __name__ == '__main__' : n = 4 res = nQueen ( n ) for temp in res : print ( temp )
C# // C# program to find all solutions of the N-Queens problem // using backtracking and pruning using System ; using System.Collections.Generic ; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil ( int j int n List < int > board bool [] rows bool [] diag1 bool [] diag2 List < List < int >> res ) { if ( j > n ) { // A solution is found res . Add ( new List < int > ( board )); return ; } for ( int i = 1 ; i <= n ; ++ i ) { if ( ! rows [ i ] && ! diag1 [ i + j ] && ! diag2 [ i - j + n ]) { // Place queen rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = true ; board . Add ( i ); // Recurse to the next column nQueenUtil ( j + 1 n board rows diag1 diag2 res ); // Remove queen (backtrack) board . RemoveAt ( board . Count - 1 ); rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = false ; } } } // Solves the N-Queens problem and returns // all valid configurations. static List < List < int >> nQueen ( int n ) { List < List < int >> res = new List < List < int >> (); List < int > board = new List < int > (); // Rows occupied bool [] rows = new bool [ n + 1 ]; // Major diagonals (row + j) and Minor diagonals (row - col + n) bool [] diag1 = new bool [ 2 * n + 1 ]; bool [] diag2 = new bool [ 2 * n + 1 ]; // Start solving from the first column nQueenUtil ( 1 n board rows diag1 diag2 res ); return res ; } static void Main ( string [] args ) { int n = 4 ; List < List < int >> res = nQueen ( n ); foreach ( var temp in res ) { Console . WriteLine ( '[' + String . Join ( ' ' temp ) + ']' ); } } }
JavaScript // JavaScript program to find all solutions of the N-Queens problem // using backtracking and pruning // Utility function for solving the N-Queens // problem using backtracking. function nQueenUtil ( j n board rows diag1 diag2 res ) { if ( j > n ) { // A solution is found res . push ([... board ]); return ; } for ( let i = 1 ; i <= n ; ++ i ) { if ( ! rows [ i ] && ! diag1 [ i + j ] && ! diag2 [ i - j + n ]) { // Place queen rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = true ; board . push ( i ); // Recurse to the next column nQueenUtil ( j + 1 n board rows diag1 diag2 res ); // Remove queen (backtrack) board . pop (); rows [ i ] = diag1 [ i + j ] = diag2 [ i - j + n ] = false ; } } } // Solves the N-Queens problem and returns // all valid configurations. function nQueen ( n ) { const res = []; const board = []; // Rows occupied const rows = Array ( n + 1 ). fill ( false ); // Major diagonals (row + j) and Minor diagonals (row - col + n) const diag1 = Array ( 2 * n + 1 ). fill ( false ); const diag2 = Array ( 2 * n + 1 ). fill ( false ); // Start solving from the first column nQueenUtil ( 1 n board rows diag1 diag2 res ); return res ; } // Driver Code const n = 4 ; const res = nQueen ( n ); res . forEach ( temp => console . log ( temp ));
Išvestis
[2 4 1 3] [3 1 4 2]
Laiko sudėtingumas: O(n!) Visiems generuoti permutacijas .
Pagalbinė erdvė: O(n)
[Alternatyvus metodas] – grįžimas naudojant bitų maskavimą
Norėdami toliau optimizuoti atsitraukimas požiūris, ypač jei tai didesnės vertės n galime naudoti bitų maskavimas efektyviai sekti užimtas eilutės ir įstrižainės. Bitų maskavimas leidžia naudoti sveikuosius skaičius ( eilutės ld rd ), kad galėtumėte stebėti, kurios eilutės ir įstrižainės yra užimtos, naudojant greitą bitinės operacijos greičiau skaičiavimai. Metodas išlieka toks pat, kaip ir aukščiau.
Žemiau pateikiama įgyvendinimas:
C++ //C++ program to find all solution of N queen problem //using recursion #include #include using namespace std ; // Function to check if the current placement is safe bool isSafe ( int row int col int rows int ld int rd int n ) { return ! (( rows >> row ) & 1 ) && ! (( ld >> ( row + col )) & 1 ) && ! (( rd >> ( row - col + n )) & 1 ); } // Recursive function to generate all possible permutations void nQueenUtil ( int col int n vector < int >& board vector < vector < int >>& res int rows int ld int rd ) { // If all queens are placed add into res if ( col > n ) { res . push_back ( board ); return ; } // Try placing a queen in each row // of the current column for ( int row = 1 ; row <= n ; ++ row ) { // Check if it's safe to place the queen if ( isSafe ( row col rows ld rd n )) { // Place the queen board . push_back ( row ); // Recur to place the next queen nQueenUtil ( col + 1 n board res rows | ( 1 < < row ) ( ld | ( 1 < < ( row + col ))) ( rd | ( 1 < < ( row - col + n )))); // Backtrack: remove the queen board . pop_back (); } } } // Main function to find all distinct // res to the n-queens puzzle vector < vector < int >> nQueen ( int n ) { vector < vector < int >> res ; // Current board configuration vector < int > board ; // Start solving from the first column nQueenUtil ( 1 n board res 0 0 0 ); return res ; } int main () { int n = 4 ; vector < vector < int >> res = nQueen ( n ); for ( int i = 0 ; i < res . size (); i ++ ) { cout < < '[' ; for ( int j = 0 ; j < n ; ++ j ) { cout < < res [ i ][ j ]; if ( j != n - 1 ) cout < < ' ' ; } cout < < '] n ' ; } return 0 ; }
Java // Java program to find all solution of N queen problem // using recursion import java.util.* ; class GfG { // Function to check if the current placement is safe static boolean isSafe ( int row int col int rows int ld int rd int n ) { return ! ((( rows >> row ) & 1 ) == 1 ) && ! ((( ld >> ( row + col )) & 1 ) == 1 ) && ! ((( rd >> ( row - col + n )) & 1 ) == 1 ); } // Recursive function to generate all possible permutations static void nQueenUtil ( int col int n ArrayList < Integer > board ArrayList < ArrayList < Integer >> res int rows int ld int rd ) { // If all queens are placed add into res if ( col > n ) { res . add ( new ArrayList <> ( board )); return ; } // Try placing a queen in each row // of the current column for ( int row = 1 ; row <= n ; ++ row ) { // Check if it's safe to place the queen if ( isSafe ( row col rows ld rd n )) { // Place the queen board . add ( row ); // Recur to place the next queen nQueenUtil ( col + 1 n board res rows | ( 1 < < row ) ( ld | ( 1 < < ( row + col ))) ( rd | ( 1 < < ( row - col + n )))); // Backtrack: remove the queen board . remove ( board . size () - 1 ); } } } // Main function to find all distinct // res to the n-queens puzzle static ArrayList < ArrayList < Integer >> nQueen ( int n ) { ArrayList < ArrayList < Integer >> res = new ArrayList <> (); // Current board configuration ArrayList < Integer > board = new ArrayList <> (); // Start solving from the first column nQueenUtil ( 1 n board res 0 0 0 ); return res ; } public static void main ( String [] args ) { int n = 4 ; ArrayList < ArrayList < Integer >> res = nQueen ( n ); for ( ArrayList < Integer > solution : res ) { System . out . print ( '[' ); for ( int j = 0 ; j < n ; ++ j ) { System . out . print ( solution . get ( j )); if ( j != n - 1 ) System . out . print ( ' ' ); } System . out . println ( ']' ); } } }
Python # Python program to find all solution of N queen problem # using recursion # Function to check if the current placement is safe def isSafe ( row col rows ld rd n ): return not (( rows >> row ) & 1 ) and not (( ld >> ( row + col )) & 1 ) and not (( rd >> ( row - col + n )) & 1 ) # Recursive function to generate all possible permutations def nQueenUtil ( col n board res rows ld rd ): # If all queens are placed add into res if col > n : res . append ( board [:]) return # Try placing a queen in each row # of the current column for row in range ( 1 n + 1 ): # Check if it's safe to place the queen if isSafe ( row col rows ld rd n ): # Place the queen board . append ( row ) # Recur to place the next queen nQueenUtil ( col + 1 n board res rows | ( 1 < < row ) ( ld | ( 1 < < ( row + col ))) ( rd | ( 1 < < ( row - col + n )))) # Backtrack: remove the queen board . pop () # Main function to find all distinct # res to the n-queens puzzle def nQueen ( n ): res = [] # Current board configuration board = [] # Start solving from the first column nQueenUtil ( 1 n board res 0 0 0 ) return res if __name__ == '__main__' : n = 4 res = nQueen ( n ) for solution in res : print ( '[' end = '' ) for j in range ( n ): print ( solution [ j ] end = '' ) if j != n - 1 : print ( ' ' end = '' ) print ( ']' )
C# // C# program to find all solution of N queen problem // using recursion using System ; using System.Collections.Generic ; class GfG { // Function to check if the current placement is safe static bool isSafe ( int row int col int rows int ld int rd int n ) { return ! ((( rows >> row ) & 1 ) == 1 ) && ! ((( ld >> ( row + col )) & 1 ) == 1 ) && ! ((( rd >> ( row - col + n )) & 1 ) == 1 ); } // Recursive function to generate all possible permutations static void nQueenUtil ( int col int n List < int > board List < List < int >> res int rows int ld int rd ) { // If all queens are placed add into res if ( col > n ) { res . Add ( new List < int > ( board )); return ; } // Try placing a queen in each row // of the current column for ( int row = 1 ; row <= n ; ++ row ) { // Check if it's safe to place the queen if ( isSafe ( row col rows ld rd n )) { // Place the queen board . Add ( row ); // Recur to place the next queen nQueenUtil ( col + 1 n board res rows | ( 1 < < row ) ( ld | ( 1 < < ( row + col ))) ( rd | ( 1 < < ( row - col + n )))); // Backtrack: remove the queen board . RemoveAt ( board . Count - 1 ); } } } // Main function to find all distinct // res to the n-queens puzzle static List < List < int >> nQueen ( int n ) { List < List < int >> res = new List < List < int >> (); // Current board configuration List < int > board = new List < int > (); // Start solving from the first column nQueenUtil ( 1 n board res 0 0 0 ); return res ; } static void Main () { int n = 4 ; List < List < int >> res = nQueen ( n ); foreach ( var solution in res ) { Console . Write ( '[' ); for ( int j = 0 ; j < n ; ++ j ) { Console . Write ( solution [ j ]); if ( j != n - 1 ) Console . Write ( ' ' ); } Console . WriteLine ( ']' ); } } }
JavaScript // JavaScript program to find all solution of N queen problem // using recursion // Function to check if the current placement is safe function isSafe ( row col rows ld rd n ) { return ! (( rows >> row ) & 1 ) && ! (( ld >> ( row + col )) & 1 ) && ! (( rd >> ( row - col + n )) & 1 ); } // Recursive function to generate all possible permutations function nQueenUtil ( col n board res rows ld rd ) { // If all queens are placed add into res if ( col > n ) { res . push ([... board ]); return ; } // Try placing a queen in each row // of the current column for ( let row = 1 ; row <= n ; ++ row ) { // Check if it's safe to place the queen if ( isSafe ( row col rows ld rd n )) { // Place the queen board . push ( row ); // Recur to place the next queen nQueenUtil ( col + 1 n board res rows | ( 1 < < row ) ( ld | ( 1 < < ( row + col ))) ( rd | ( 1 < < ( row - col + n )))); // Backtrack: remove the queen board . pop (); } } } // Main function to find all distinct // res to the n-queens puzzle function nQueen ( n ) { let res = []; // Current board configuration let board = []; // Start solving from the first column nQueenUtil ( 1 n board res 0 0 0 ); return res ; } // Driver Code let n = 4 ; let res = nQueen ( n ); for ( let i = 0 ; i < res . length ; i ++ ) { process . stdout . write ( '[' ); for ( let j = 0 ; j < n ; ++ j ) { process . stdout . write ( res [ i ][ j ]. toString ()); if ( j !== n - 1 ) process . stdout . write ( ' ' ); } console . log ( ']' ); }
Išvestis
[2 4 1 3] [3 1 4 2]
Laiko sudėtingumas: O(n!) visų permutacijų generavimui.
Erdvės sudėtingumas: O(n)