Atspausdinkite visus būdus, kaip sulaužyti eilutę laikiklio forma
Suteikus eilutę, raskite visus būdus, kaip sulaužyti duotą eilutę laikiklio formoje. Kiekvieną substringą uždenkite skliausteliuose.
Pavyzdžiai:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Mes labai rekomenduojame sumažinti savo naršyklę ir pirmiausia išbandyti tai patys.
Idėja yra naudoti rekursiją. Mes palaikome du parametrus - kito simbolio, kurį reikia apdoroti, rodyklė ir išvesties eilutė iki šiol. Mes pradedame nuo kito simbolio rodyklės, kad būtų apdorojami priedų eilutė, suformuota neapdorota eilutė iki išvesties eilutės, ir pakartokite likusią eilutę, kol apdorosime visą eilutę. Išvesties eilutei suformuojame STD :: substr. Substr (POS N) Grąžina ilgio N ilgį, kuris prasideda dabartinės eilutės padėties POS.
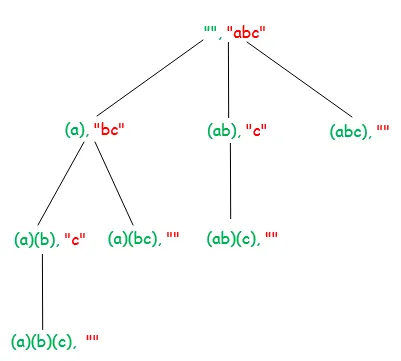
Žemiau esančioje diagramoje parodytas įvesties eilutės „ABC“ rekursinis medis. Kiekvienas diagramos mazgas rodo apdorotą eilutę (pažymėtą žalia) ir neapdorota eilutė (pažymėta raudona spalva).
Žemiau yra aukščiau pateiktos idėjos įgyvendinimas
C++ // C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include using namespace std ; // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far void findCombinations ( string str int index string out ) { if ( index == str . length ()) cout < < out < < endl ; for ( int i = index ; i < str . length (); i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substr ( index i + 1 - index ) + ')' ); } } // Driver Code int main () { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); return 0 ; }
Java // Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations ( String str int index String out ) { if ( index == str . length ()) System . out . println ( out ); for ( int i = index ; i < str . length (); i ++ ) // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substring ( index i + 1 ) + ')' ); } // Driver Code public static void main ( String [] args ) { // input string String str = 'abcd' ; findCombinations ( str 0 '' ); } } // Contributed by Pramod Kumar
Python3 # Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations ( string index out ): if index == len ( string ): print ( out ) for i in range ( index len ( string ) 1 ): # append substring formed by str[index # i] to output string findCombinations ( string i + 1 out + '(' + string [ index : i + 1 ] + ')' ) # Driver Code if __name__ == '__main__' : # input string string = 'abcd' findCombinations ( string 0 '' ) # This code is contributed by # sanjeev2552
C# // C# program to find all combinations // of Non-overlapping substrings formed // from given string using System ; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations ( string str int index string @out ) { if ( index == str . Length ) { Console . WriteLine ( @out ); } for ( int i = index ; i < str . Length ; i ++ ) { // append substring formed by // str[index i] to output string findCombinations ( str i + 1 @out + '(' + str . Substring ( index ( i + 1 ) - index ) + ')' ); } } // Driver Code public static void Main ( string [] args ) { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); } } // This code is contributed by Shrikant13
JavaScript // Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations ( string index out ) { if ( index == string . length ) { console . log ( out ); } for ( let i = index ; i < string . length ; i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( string i + 1 out + '(' + string . substring ( index i + 1 ) + ')' ); } } // Driver Code const string = 'abcd' ; findCombinations ( string 0 '' ); // contributed by adityasharmadev01
Išvestis
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Laiko sudėtingumas: o (n 2 )
Pagalbinė erdvė: o (n 2 )
