Ilgiausia bendra eilutė | DP-29
Atsižvelgdami į dvi eilutes „X“ ir „Y“, suraskite ilgiausios bendros poeilutės ilgį.
Pavyzdžiai:
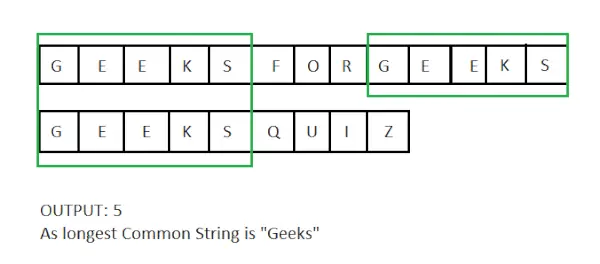
Įvestis: X = techcodeview.com, y = GeeksQuiz
Išvestis : 5
Paaiškinimas:
Ilgiausia įprasta poeilutė yra Geeks ir yra 5 ilgio.Įvestis: X = abcdxyz, y = xyzabcd
Išvestis: 4
Paaiškinimas:
Ilgiausia bendra eilutė yra abcd ir yra 4 ilgio.Įvestis: X = zxabcdezy, y = yzabcdezx
Išvestis: 6
Paaiškinimas:
Ilgiausia įprasta poeilutė yra abcdez ir yra 6 ilgio.

Metodas:
Tegul m ir n yra atitinkamai pirmosios ir antrosios eilučių ilgiai.
A paprastas sprendimas yra po vieną apsvarstykite visas pirmosios eilutės eilutes ir kiekvieną eilutę patikrinkite, ar tai yra antrosios eilutės poeilutė. Stebėkite maksimalaus ilgio eilutę. Bus O(m^2) poeilutės ir mes galime sužinoti, ar eilutė yra kitos eilutės poeilutė per O(n) laiką (žr. tai ). Taigi bendras šio metodo laiko sudėtingumas būtų O (n * m 2 )
Dinaminis programavimas galima naudoti norint rasti ilgiausią bendrą eilutę per O(m*n) laiką. Idėja yra rasti ilgiausios bendros priesagos ilgį visoms abiejų eilučių poeilėms ir išsaugoti šiuos ilgius lentelėje.
Ilgiausia bendra priesaga turi optimalią postruktūros savybę.
Jei paskutiniai simboliai sutampa, abu ilgius sumažiname 1
- LCSefektas(X, Y, m, n) = LCSefektas(X, Y, m-1, n-1) + 1, jei X[m-1] = Y[n-1]
Jei paskutiniai simboliai nesutampa, rezultatas yra 0, t.y.
- LCSuff(X, Y, m, n) = 0, jei (X[m-1] != Y[n-1])
Dabar nagrinėjame skirtingų poeilučių priesagas, kurios baigiasi skirtingais indeksais.
Maksimalus ilgis Longest Common Sufiksa yra ilgiausia bendroji poeilutė.
LCSubStr(X, Y, m, n) = maks.(LCSuff(X, Y, i, j)) kur 1 <= i <= m ir 1 <= j <= n
Toliau pateikiamas iteracinis aukščiau pateikto sprendimo įgyvendinimas.
C++
/* Dynamic Programming solution to> > find length of the> > longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> > common substring of X[0..m-1]> > and Y[0..n-1] */> int> LCSubStr(> char> * X,> char> * Y,> int> m,> int> n)> {> > // Create a table to store> > // lengths of longest> > // common suffixes of substrings.> > // Note that LCSuff[i][j] contains> > // length of longest common suffix> > // of X[0..i-1] and Y[0..j-1].> > int> LCSuff[m + 1][n + 1];> > int> result = 0;> // To store length of the> > // longest common substring> > /* Following steps build LCSuff[m+1][n+1] in> > bottom up fashion. */> > for> (> int> i = 0; i <= m; i++)> > {> > for> (> int> j = 0; j <= n; j++)> > {> > // The first row and first column> > // entries have no logical meaning,> > // they are used only for simplicity> > // of program> > if> (i == 0 || j == 0)> > LCSuff[i][j] = 0;> > else> if> (X[i - 1] == Y[j - 1]) {> > LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> > result = max(result, LCSuff[i][j]);> > }> > else> > LCSuff[i][j] = 0;> > }> > }> > return> result;> }> // Driver code> int> main()> {> > char> X[] => 'OldSite:techcodeview.com.org'> ;> > char> Y[] => 'NewSite:GeeksQuiz.com'> ;> > int> m => strlen> (X);> > int> n => strlen> (Y);> > cout < <> 'Length of Longest Common Substring is '> > < < LCSubStr(X, Y, m, n);> > return> 0;> }> |
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> > /*> > Returns length of longest common substring> > of X[0..m-1] and Y[0..n-1]> > */> > static> int> LCSubStr(> char> X[],> char> Y[],> int> m,> int> n)> > {> > // Create a table to store> > // lengths of longest common> > // suffixes of substrings.> > // Note that LCSuff[i][j]> > // contains length of longest> > // common suffix of> > // X[0..i-1] and Y[0..j-1].> > // The first row and first> > // column entries have no> > // logical meaning, they are> > // used only for simplicity of program> > int> LCStuff[][] => new> int> [m +> 1> ][n +> 1> ];> > // To store length of the longest> > // common substring> > int> result => 0> ;> > // Following steps build> > // LCSuff[m+1][n+1] in bottom up fashion> > for> (> int> i => 0> ; i <= m; i++) {> > for> (> int> j => 0> ; j <= n; j++) {> > if> (i ==> 0> || j ==> 0> )> > LCStuff[i][j] => 0> ;> > else> if> (X[i -> 1> ] == Y[j -> 1> ]) {> > LCStuff[i][j]> > = LCStuff[i -> 1> ][j -> 1> ] +> 1> ;> > result = Integer.max(result,> > LCStuff[i][j]);> > }> > else> > LCStuff[i][j] => 0> ;> > }> > }> > return> result;> > }> > // Driver Code> > public> static> void> main(String[] args)> > {> > String X => 'OldSite:techcodeview.com.org'> ;> > String Y => 'NewSite:GeeksQuiz.com'> ;> > int> m = X.length();> > int> n = Y.length();> > System.out.println(> > 'Length of Longest Common Substring is '> > + LCSubStr(X.toCharArray(), Y.toCharArray(), m,> > n));> > }> }> // This code is contributed by Sumit Ghosh> |
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> > # Create a table to store lengths of> > # longest common suffixes of substrings.> > # Note that LCSuff[i][j] contains the> > # length of longest common suffix of> > # X[0...i-1] and Y[0...j-1]. The first> > # row and first column entries have no> > # logical meaning, they are used only> > # for simplicity of the program.> > # LCSuff is the table with zero> > # value initially in each cell> > LCSuff> => [[> 0> for> k> in> range> (n> +> 1> )]> for> l> in> range> (m> +> 1> )]> > # To store the length of> > # longest common substring> > result> => 0> > # Following steps to build> > # LCSuff[m+1][n+1] in bottom up fashion> > for> i> in> range> (m> +> 1> ):> > for> j> in> range> (n> +> 1> ):> > if> (i> => => 0> or> j> => => 0> ):> > LCSuff[i][j]> => 0> > elif> (X[i> -> 1> ]> => => Y[j> -> 1> ]):> > LCSuff[i][j]> => LCSuff[i> -> 1> ][j> -> 1> ]> +> 1> > result> => max> (result, LCSuff[i][j])> > else> :> > LCSuff[i][j]> => 0> > return> result> # Driver Code> X> => 'OldSite:techcodeview.com.org'> Y> => 'NewSite:GeeksQuiz.com'> m> => len> (X)> n> => len> (Y)> print> (> 'Length of Longest Common Substring is'> ,> > LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> > // Returns length of longest common> > // substring of X[0..m-1] and Y[0..n-1]> > static> int> LCSubStr(> string> X,> string> Y,> int> m,> int> n)> > {> > // Create a table to store lengths of> > // longest common suffixes of substrings.> > // Note that LCSuff[i][j] contains length> > // of longest common suffix of X[0..i-1]> > // and Y[0..j-1]. The first row and first> > // column entries have no logical meaning,> > // they are used only for simplicity of> > // program> > int> [, ] LCStuff => new> int> [m + 1, n + 1];> > // To store length of the longest common> > // substring> > int> result = 0;> > // Following steps build LCSuff[m+1][n+1]> > // in bottom up fashion> > for> (> int> i = 0; i <= m; i++)> > {> > for> (> int> j = 0; j <= n; j++)> > {> > if> (i == 0 || j == 0)> > LCStuff[i, j] = 0;> > else> if> (X[i - 1] == Y[j - 1])> > {> > LCStuff[i, j]> > = LCStuff[i - 1, j - 1] + 1;> > result> > = Math.Max(result, LCStuff[i, j]);> > }> > else> > LCStuff[i, j] = 0;> > }> > }> > return> result;> > }> > // Driver Code> > public> static> void> Main()> > {> > String X => 'OldSite:techcodeview.com.org'> ;> > String Y => 'NewSite:GeeksQuiz.com'> ;> > int> m = X.Length;> > int> n = Y.Length;> > Console.Write(> 'Length of Longest Common'> > +> ' Substring is '> > + LCSubStr(X, Y, m, n));> > }> }> // This code is contributed by Sam007.> |
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> > /*> > Returns length of longest common> > substring of X[0..m-1] and Y[0..n-1]> > */> > function> LCSubStr( X, Y , m , n) {> > // Create a table to store> > // lengths of longest common> > // suffixes of substrings.> > // Note that LCSuff[i][j]> > // contains length of longest> > // common suffix of> > // X[0..i-1] and Y[0..j-1].> > // The first row and first> > // column entries have no> > // logical meaning, they are> > // used only for simplicity of program> > > var> LCStuff => > Array(m + 1).fill().map(()=>Masyvas(n + 1).fill(0));> > // To store length of the longest> > // common substring> > var> result = 0;> > // Following steps build> > // LCSuff[m+1][n+1] in bottom up fashion> > for> (i = 0; i <= m; i++) {> > for> (j = 0; j <= n; j++) {> > if> (i == 0 || j == 0)> > LCStuff[i][j] = 0;> > else> if> (X[i - 1] == Y[j - 1]) {> > LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> > result = Math.max(result, LCStuff[i][j]);> > }> else> > LCStuff[i][j] = 0;> > }> > }> > return> result;> > }> > // Driver Code> > > var> X => 'OldSite:techcodeview.com.org'> ;> > var> Y => 'NewSite:GeeksQuiz.com'> ;> > var> m = X.length;> > var> n = Y.length;> > document.write(> 'Length of Longest Common Substring is '> +> > LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>>> |
>
Laiko sudėtingumas: O(m*n)
Pagalbinė erdvė: O(m*n), nes buvo užimta m*n papildomos vietos.Kitas požiūris: (Optimizuotas požiūris į erdvę).
Taikant aukščiau pateiktą metodą, mes naudojame tik paskutinę 2-D masyvo eilutę, todėl galime optimizuoti erdvę naudodami
2 matmenų 2* (min(n,m)) 2D masyvas.Žemiau pateikiamas pirmiau minėto metodo įgyvendinimas:
C++
#include>#include>using>namespace>std;>// Function to find the length of the longest LCS>int>LCSubStr(string s, string t,>int>n,>int>m)>{>>// Create DP table>>vectorint>> dp(n + 1, vektorius(m + 1, 0)); int res = 0; už (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { if (s[i - 1] == t[j - 1]) { dp[i][j] = dp[i - 1][j - 1] + 1; if (dp[i][j]>res) res = dp[i][j]; } else dp[i][j] = 0; } } return res; } // Tvarkyklės kodas int main() { string X = 'dddabcaafdgssfdgsdg'; eilutė Y = 'bbbabcdeffffffff'; int m = X.ilgis(); int n = Y.ilgis(); cout < < LCSubStr(X, Y, m, n); return 0; }>
Java
// Java implementation of the above approach>import>java.io.*;>class>GFG>{>>>// Function to find the length of the>>// longest LCS>>static>int>LCSubStr(String s,String t,>>int>n,>int>m)>>{>>>// Create DP table>>int>dp[][]=>new>int>[>2>][m+>1>];>>int>res=>0>;>>>for>(>int>i=>1>;i <=n;i++)>>{>>for>(>int>j=>1>;j <=m;j++)>>{>>if>(s.charAt(i->1>)==t.charAt(j->1>))>>{>>dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;>>if>(dp[i%>2>][j]>res)>>res=dp[i%>2>][j];>>}>>else>dp[i%>2>][j]=>0>;>>}>>}>>return>res;>>}>>>// Driver Code>>public>static>void>main (String[] args)>>{>>String X=>'OldSite:techcodeview.com.org'>;>>String Y=>'NewSite:GeeksQuiz.com'>;>>>int>m=X.length();>>int>n=Y.length();>>>// Function call>>System.out.println(LCSubStr(X,Y,m,n));>>>}>}>
Python3
# Python implementation of the above approach># Function to find the length of the># longest LCS>def>LCSubStr(s, t, n, m):>>># Create DP table>>dp>=>[[>0>for>i>in>range>(m>+>1>)]>for>j>in>range>(>2>)]>>res>=>0>>>for>i>in>range>(>1>,n>+>1>):>>for>j>in>range>(>1>,m>+>1>):>>if>(s[i>->1>]>=>=>t[j>->1>]):>>dp[i>%>2>][j]>=>dp[(i>->1>)>%>2>][j>->1>]>+>1>>if>(dp[i>%>2>][j]>res):>>res>=>dp[i>%>2>][j]>>else>:>>dp[i>%>2>][j]>=>0>>return>res># Driver Code>X>=>'OldSite:techcodeview.com.org'>Y>=>'NewSite:GeeksQuiz.com'>m>=>len>(X)>n>=>len>(Y)># Function call>print>(LCSubStr(X,Y,m,n))># This code is contributed by avanitrachhadiya2155>
C#
// C# implementation of the above approach>using>System;>public>class>GFG>{>>// Function to find the length of the>>// longest LCS>>static>int>LCSubStr(>string>s,>string>t,>>int>n,>int>m)>>{>>// Create DP table>>int>[,] dp =>new>int>[2, m + 1];>>int>res = 0;>>for>(>int>i = 1; i <= n; i++)>>{>>for>(>int>j = 1; j <= m; j++)>>{>>if>(s[i - 1] == t[j - 1])>>{>>dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;>>if>(dp[i % 2, j]>res)>>res = dp[i % 2, j];>>}>>else>dp[i % 2, j] = 0;>>}>>}>>return>res;>>}>>// Driver Code>>static>public>void>Main (){>>string>X =>'OldSite:techcodeview.com.org'>;>>string>Y =>'NewSite:GeeksQuiz.com'>;>>int>m = X.Length;>>int>n = Y.Length;>>// Function call>>Console.WriteLine(LCSubStr(X,Y,m,n));>>}>}>// This code is contributed by rag2127>
Javascript
>// JavaScript implementation of the above approach>>// Function to find the length of the>>// longest LCS>>function>LCSubStr(s, t, n, m)>>{>>>// Create DP table>>var>dp = Array(2).fill().map(()=>Masyvas(m+ 1).fill(0));>>var>res = 0;>>>for>(>var>i = 1; i <= n; i++)>>{>>for>(>var>j = 1; j <= m; j++)>>{>>if>(s.charAt(i - 1) == t.charAt(j - 1))>>{>>dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;>>if>(dp[i % 2][j]>res)>>res = dp[i % 2][j];>>}>>else>dp[i % 2][j] = 0;>>}>>}>>return>res;>>}>>>// Driver Code>>var>X =>'OldSite:techcodeview.com.org'>;>>var>Y =>'NewSite:GeeksQuiz.com'>;>>>var>m = X.length;>>var>n = Y.length;>>>// Function call>>document.write(LCSubStr(X, Y, m, n));>// This code is contributed by shivanisinghss2110>>
Išvestis
10Laiko sudėtingumas: O(n*m)
Pagalbinė erdvė: O(min(m,n))Kitas požiūris: (Naudojama rekursija)
Čia yra pirmiau pateikto metodo rekursinis sprendimas.C++
// C++ program using to find length of the>// longest common substring recursion>#include>using>namespace>std;>string X, Y;>// Returns length of function f>// or longest common substring>// of X[0..m-1] and Y[0..n-1]>int>lcs(>int>i,>int>j,>int>count)>{>>if>(i == 0 || j == 0)>>return>count;>>if>(X[i - 1] == Y[j - 1]) {>>count = lcs(i - 1, j - 1, count + 1);>>}>>count = max(count,>>max(lcs(i, j - 1, 0),>>lcs(i - 1, j, 0)));>>return>count;>}>// Driver code>int>main()>{>>int>n, m;>>X =>'abcdxyz'>;>>Y =>'xyzabcd'>;>>n = X.size();>>m = Y.size();>>cout < < lcs(n, m, 0);>>return>0;>}>
Java
// Java program using to find length of the>// longest common substring recursion>import>java.io.*;>class>GFG {>>static>String X, Y;>>// Returns length of function>>// for longest common>>// substring of X[0..m-1] and Y[0..n-1]>>static>int>lcs(>int>i,>int>j,>int>count)>>{>>if>(i ==>0>|| j ==>0>)>>{>>return>count;>>}>>if>(X.charAt(i ->1>)>>== Y.charAt(j ->1>))>>{>>count = lcs(i ->1>, j ->1>, count +>1>);>>}>>count = Math.max(count,>>Math.max(lcs(i, j ->1>,>0>),>>lcs(i ->1>, j,>0>)));>>return>count;>>}>>>// Driver code>>public>static>void>main(String[] args)>>{>>int>n, m;>>X =>'abcdxyz'>;>>Y =>'xyzabcd'>;>>n = X.length();>>m = Y.length();>>System.out.println(lcs(n, m,>0>));>>}>}>// This code is contributed by Rajput-JI>
Python3
# Python3 program using to find length of># the longest common substring recursion># Returns length of function for longest># common substring of X[0..m-1] and Y[0..n-1]>def>lcs(i, j, count):>>if>(i>=>=>0>or>j>=>=>0>):>>return>count>>if>(X[i>->1>]>=>=>Y[j>->1>]):>>count>=>lcs(i>->1>, j>->1>, count>+>1>)>>count>=>max>(count,>max>(lcs(i, j>->1>,>0>),>>lcs(i>->1>, j,>0>)))>>return>count># Driver code>if>__name__>=>=>'__main__'>:>>X>=>'abcdxyz'>>Y>=>'xyzabcd'>>n>=>len>(X)>>m>=>len>(Y)>>print>(lcs(n, m,>0>))># This code is contributed by Ryuga>
C#
// C# program using to find length>// of the longest common substring>// recursion>using>System;>class>GFG {>>static>String X, Y;>>// Returns length of function for>>// longest common substring of>>// X[0..m-1] and Y[0..n-1]>>static>int>lcs(>int>i,>int>j,>int>count)>>{>>if>(i == 0 || j == 0) {>>return>count;>>}>>if>(X[i - 1] == Y[j - 1]) {>>count = lcs(i - 1, j - 1, count + 1);>>}>>count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),>>lcs(i - 1, j, 0)));>>return>count;>>}>>// Driver code>>public>static>void>Main()>>{>>int>n, m;>>X =>'abcdxyz'>;>>Y =>'xyzabcd'>;>>n = X.Length;>>m = Y.Length;>>Console.Write(lcs(n, m, 0));>>}>}>// This code is contributed by Rajput-JI>
Javascript
>>// Javascript program using to find length of the>>// longest common substring recursion>>let X, Y;>>>// Returns length of function f>>// or longest common substring>>// of X[0..m-1] and Y[0..n-1]>>function>lcs(i, j, count)>>{>>>if>(i == 0 || j == 0)>>return>count;>>>if>(X[i - 1] == Y[j - 1]) {>>count = lcs(i - 1, j - 1, count + 1);>>}>>count = Math.max(count,>>Math.max(lcs(i, j - 1, 0),>>lcs(i - 1, j, 0)));>>return>count;>>}>>>let n, m;>>>X =>'abcdxyz'>;>>Y =>'xyzabcd'>;>>>n = X.length;>>m = Y.length;>>>document.write(lcs(n, m, 0));>>>// This code is contributed by divyeshrabadiya07.>>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>>>
>
Laiko sudėtingumas : O(2^maks.(m,n)) nes funkcija atlieka du rekursinius iškvietimus – lcs(i, j-1, 0) ir lcs(i-1, j, 0), kai simboliai X[i-1] != Y[j-1]. Taigi tai duos blogiausio atvejo laiko sudėtingumą kaip 2^N, kur N = max(m, n), m ir n yra X ir Y eilutės ilgis.
Pagalbinė erdvė: O(1): nes funkcijos iškvietimas nenaudoja jokios papildomos vietos (funkcija naudoja tik rekursinį iškvietimo krūvą, kurio mes paprastai nenagrinėjame pagalbinėje erdvėje).Maksimalus erdvės optimizavimas :Reklama