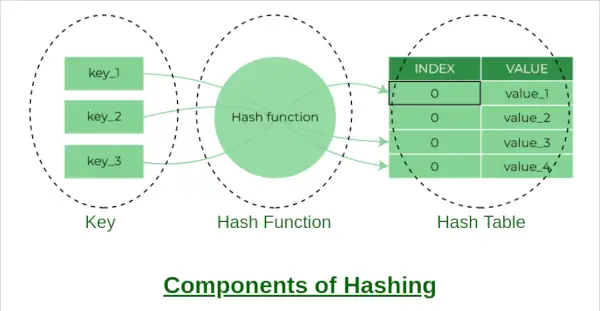
A maišos lentelė yra duomenų struktūra, leidžianti greitai įterpti, ištrinti ir gauti duomenis. Jis veikia naudojant maišos funkciją, kad susietų raktą su masyvo indeksu. Šiame straipsnyje mes įdiegsime maišos lentelę „Python“, naudodami atskirą grandininį susiejimą, kad būtų galima valdyti susidūrimus.

Maišos komponentai

Atskiras grandinės sujungimas yra metodas, naudojamas susidūrimams maišos lentelėje valdyti. Kai du ar daugiau raktų susieja su tuo pačiu indeksu masyve, saugome juos susietame sąraše tame indekse. Tai leidžia mums išsaugoti kelias vertes tame pačiame indekse ir vis tiek jas gauti naudojant jų raktą.

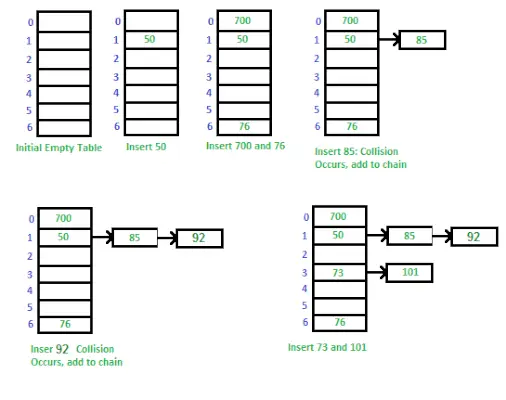
Maišos lentelės diegimo būdas naudojant atskirą grandinę

Maišos lentelės diegimo būdas naudojant atskirą grandinėjimą:

Sukurkite dvi klases: „ Mazgas 'ir' HashTable “.

„ Mazgas ‘ klasė atstovaus susieto sąrašo mazgą. Kiekviename mazge bus rakto-reikšmių pora, taip pat rodyklė į kitą sąrašo mazgą.

Python3

class> Node:> > def> __init__(> self> , key, value):> > self> .key> => key> > self> .value> => value> > self> .> next> => None>

„HashTable“ klasėje bus masyvas, kuriame bus susieti sąrašai, taip pat metodai, kaip įterpti, nuskaityti ir ištrinti duomenis iš maišos lentelės.

Python3

class> HashTable:> > def> __init__(> self> , capacity):> > self> .capacity> => capacity> > self> .size> => 0> > self> .table> => [> None> ]> *> capacity>

„ __karšta__ ' metodas inicijuoja maišos lentelę tam tikra talpa. Jis nustato „ talpa 'ir' dydis “ kintamuosius ir inicijuoja masyvą į „Nėra“.

Kitas metodas yra „ _hash ‘metodas. Šis metodas paima raktą ir grąžina indeksą masyve, kuriame turėtų būti saugoma rakto ir reikšmės pora. Mes naudosime Python integruotą maišos funkciją raktui maišyti, o tada naudosime operatorių modulo, kad gautume indeksą masyve.

Python3

def> _hash(> self> , key):> > return> hash> (key)> %> self> .capacity>

The 'Įdėti' metodas įterps rakto-reikšmių porą į maišos lentelę. Tam reikia indekso, kuriame pora turėtų būti saugoma naudojant „ _hash ‘metodas. Jei tame indekse nėra susieto sąrašo, jis sukuria naują mazgą su raktų ir reikšmių pora ir nustato jį kaip sąrašo antraštę. Jei tame indekse yra susietas sąrašas, kartokite sąrašą, kol bus rastas paskutinis mazgas arba raktas jau egzistuoja, ir atnaujinkite reikšmę, jei raktas jau yra. Jei randa raktą, jis atnaujina vertę. Jei jis neranda rakto, jis sukuria naują mazgą ir prideda jį prie sąrašo pradžios.

Python3

def> insert(> self> , key, value):> > index> => self> ._hash(key)> > if> self> .table[index]> is> None> :> > self> .table[index]> => Node(key, value)> > self> .size> +> => 1> > else> :> > current> => self> .table[index]> > while> current:> > if> current.key> => => key:> > current.value> => value> > return> > current> => current.> next> > new_node> => Node(key, value)> > new_node.> next> => self> .table[index]> > self> .table[index]> => new_node> > self> .size> +> => 1>

The Paieška metodas nuskaito vertę, susietą su duotu raktu. Pirmiausia jis gauna indeksą, kuriame turėtų būti saugoma raktų ir reikšmių pora, naudojant _hash metodas. Tada jis ieško rakto susietame sąraše toje rodyklėje. Jei randa raktą, jis grąžina susijusią reikšmę. Jei neranda rakto, jis pakelia a Key Error .

Python3

def> search(> self> , key):> > index> => self> ._hash(key)> > current> => self> .table[index]> > while> current:> > if> current.key> => => key:> > return> current.value> > current> => current.> next> > raise> KeyError(key)>

The 'pašalinti' metodas pašalina rakto-reikšmių porą iš maišos lentelės. Pirmiausia jis gauna indeksą, kuriame pora turėtų būti saugoma naudojant ` _hash ` metodas. Tada jis ieško rakto susietame sąraše toje rodyklėje. Jei jis randa raktą, jis pašalina mazgą iš sąrašo. Jei jis neranda rakto, jis pakelia ` Key Error `.

Python3

def> remove(> self> , key):> > index> => self> ._hash(key)> > > previous> => None> > current> => self> .table[index]> > > while> current:> > if> current.key> => => key:> > if> previous:> > previous.> next> => current.> next> > else> :> > self> .table[index]> => current.> next> > self> .size> -> => 1> > return> > previous> => current> > current> => current.> next> > > raise> KeyError(key)>

„__str__“ metodas, kuris grąžina maišos lentelės eilutę.

Python3

def> __str__(> self> ):> > elements> => []> > for> i> in> range> (> self> .capacity):> > current> => self> .table[i]> > while> current:> > elements.append((current.key, current.value))> > current> => current.> next> > return> str> (elements)>

Štai visas „HashTable“ klasės įgyvendinimas:

Python3

class> Node:> > def> __init__(> self> , key, value):> > self> .key> => key> > self> .value> => value> > self> .> next> => None> > > class> HashTable:> > def> __init__(> self> , capacity):> > self> .capacity> => capacity> > self> .size> => 0> > self> .table> => [> None> ]> *> capacity> > > def> _hash(> self> , key):> > return> hash> (key)> %> self> .capacity> > > def> insert(> self> , key, value):> > index> => self> ._hash(key)> > > if> self> .table[index]> is> None> :> > self> .table[index]> => Node(key, value)> > self> .size> +> => 1> > else> :> > current> => self> .table[index]> > while> current:> > if> current.key> => => key:> > current.value> => value> > return> > current> => current.> next> > new_node> => Node(key, value)> > new_node.> next> => self> .table[index]> > self> .table[index]> => new_node> > self> .size> +> => 1> > > def> search(> self> , key):> > index> => self> ._hash(key)> > > current> => self> .table[index]> > while> current:> > if> current.key> => => key:> > return> current.value> > current> => current.> next> > > raise> KeyError(key)> > > def> remove(> self> , key):> > index> => self> ._hash(key)> > > previous> => None> > current> => self> .table[index]> > > while> current:> > if> current.key> => => key:> > if> previous:> > previous.> next> => current.> next> > else> :> > self> .table[index]> => current.> next> > self> .size> -> => 1> > return> > previous> => current> > current> => current.> next> > > raise> KeyError(key)> > > def> __len__(> self> ):> > return> self> .size> > > def> __contains__(> self> , key):> > try> :> > self> .search(key)> > return> True> > except> KeyError:> > return> False> > > # Driver code> if> __name__> => => '__main__'> :> > > # Create a hash table with> > # a capacity of 5> > ht> => HashTable(> 5> )> > > # Add some key-value pairs> > # to the hash table> > ht.insert(> 'apple'> ,> 3> )> > ht.insert(> 'banana'> ,> 2> )> > ht.insert(> 'cherry'> ,> 5> )> > > # Check if the hash table> > # contains a key> > print> (> 'apple'> in> ht)> # True> > print> (> 'durian'> in> ht)> # False> > > # Get the value for a key> > print> (ht.search(> 'banana'> ))> # 2> > > # Update the value for a key> > ht.insert(> 'banana'> ,> 4> )> > print> (ht.search(> 'banana'> ))> # 4> > > ht.remove(> 'apple'> )> > # Check the size of the hash table> > print> (> len> (ht))> # 3>

Išvestis

True False 2 4 3 

Laiko ir erdvės sudėtingumas:

• The laiko sudėtingumas iš Įdėti , Paieška ir pašalinti metodai maišos lentelėje, naudojant atskirą grandinę, priklauso nuo maišos lentelės dydžio, raktų ir reikšmių porų skaičiaus maišos lentelėje ir susieto sąrašo ilgio kiekviename indekse.
• Darant prielaidą, kad gera maišos funkcija ir vienodas raktų pasiskirstymas, numatomas šių metodų sudėtingumas O(1) kiekvienai operacijai. Tačiau blogiausiu atveju laikas gali būti sudėtingas O(n) , kur n yra raktų ir reikšmių porų skaičius maišos lentelėje.
• Tačiau svarbu pasirinkti gerą maišos funkciją ir tinkamą maišos lentelės dydį, kad sumažintumėte susidūrimų tikimybę ir užtikrintumėte gerą veikimą.
• The erdvės sudėtingumas maišos lentelės, naudojant atskirą grandinę, dydis priklauso nuo maišos lentelės dydžio ir maišos lentelėje saugomų raktų ir reikšmių porų skaičiaus.
• Pati maišos lentelė ima O(m) erdvė, kur m yra maišos lentelės talpa. Kiekvienas susietas sąrašo mazgas užima O(1) tarpo, o susietuose sąrašuose gali būti daugiausia n mazgų, kur n yra maišos lentelėje saugomų raktų ir reikšmių porų skaičius.
• Todėl bendras erdvės sudėtingumas yra O(m + n) .

Išvada:

Praktikoje svarbu pasirinkti tinkamą maišos lentelės talpą, kad būtų subalansuotas erdvės naudojimas ir susidūrimų tikimybė. Jei talpa per maža, padidėja susidūrimų tikimybė, o tai gali sukelti našumo pablogėjimą. Kita vertus, jei talpa per didelė, maišos lentelė gali sunaudoti daugiau atminties nei reikia.