Raskite, ar duota matrica yra Toeplitz, ar ne
Duota kvadratinė matrica kartu su [][] tvarkos n jūsų užduotis yra patikrinti, ar tai „Toeplitz Matrix“.
Pastaba: Toeplitzo matrica, dar vadinama įstrižainės pastoviąja matrica, yra matrica, kurioje kiekvienos atskiros mažėjančios įstrižainės elementai yra vienodi iš kairės į dešinę. Lygiai taip pat bet kokiam įėjimo kilimėliui[i][j] jis yra toks pat kaip mat[i-1][j-1] arba kilimėliui[i-2][j-2] ir ant jo.
Pavyzdžiai:
Įvestis: su [][] = [ [6 7 8]
[4 6 7]
[1 4 6] ]
Išvestis: Taip
Paaiškinimas: Visos pateiktos matricos įstrižainės yra [6 6 6] [7 7] [8] [4 4] [1]. Kiekvienai įstrižai, nes visi elementai yra vienodi, duota matrica yra Toeplitz matrica.Įvestis: su [][] = [ [6 3 8]
[4 9 7]
[1 4 6] ]
Išvestis: Nr
Paaiškinimas: Pirminiai duotosios matricos įstrižainės elementai yra [6 9 6]. Kadangi įstrižainės elementai nėra vienodi, pateikta matrica nėra Toeplitz matrica.
[Numatomas požiūris – 1] – Kiekvienos įstrižainės tikrinimas – O(n * n) laikas ir O(1) erdvė
Idėja yra pereiti kiekvieną žemyn pasvirusią matricos įstrižainę, naudojant kiekvieną elementą pirmoje eilutėje ir kiekvieną elementą pirmame stulpelyje kaip pradžios tašką ir patikrinti, ar kiekvienas elementas išilgai tos įstrižainės atitinka reikšmę jo pradžioje.
Atlikite toliau nurodytus veiksmus:
- Leiskite
n = mat.size()irm = mat[0].size(). - Kiekvienam stulpelio indeksui
iiš0įm - 1skambinticheckDiagonal(mat 0 i); jei grąžinama klaidinga, nedelsiant grąžinama klaidinga išisToeplitz. - Kiekvienai eilutės indeksui
iiš0įn - 1skambinticheckDiagonal(mat i 0); jei grąžinama klaidinga, nedelsiant grąžinama klaidinga išisToeplitz. - Jei visi skambina
checkDiagonalpavyktų grįžti tiesa. - Į
checkDiagonal(mat x y)palygintimat[i][j]įmat[x][y]kiekvienami = x+1 j = y+1koli < n && j < m; return false esant pirmam neatitikimui, kitu atveju, pasiekus kraštą, grąžinti teisingą.
Žemiau pateikiama įgyvendinimas:
C++ #include using namespace std ; // function to check if diagonal elements are same bool checkDiagonal ( vector < vector < int >> & mat int x int y ) { int n = mat . size () m = mat [ 0 ]. size (); for ( int i = x + 1 j = y + 1 ; i < n && j < m ; i ++ j ++ ) { if ( mat [ i ][ j ] != mat [ x ][ y ]) return false ; } return true ; } // Function to check whether given // matrix is toeplitz matrix or not bool isToeplitz ( vector < vector < int >> & mat ) { int n = mat . size () m = mat [ 0 ]. size (); // check each descending diagonal starting from // first row and first column of the matrix for ( int i = 0 ; i < m ; i ++ ) if ( ! checkDiagonal ( mat 0 i )) return false ; for ( int i = 0 ; i < n ; i ++ ) if ( ! checkDiagonal ( mat i 0 )) return false ; // if all diagonals are same return true return true ; } int main () { vector < vector < int >> mat = { { 6 7 8 } { 4 6 7 } { 1 4 6 } }; if ( isToeplitz ( mat )) { cout < < 'Yes' ; } else { cout < < 'No' ; } return 0 ; }
Java import java.util.* ; class GfG { // function to check if diagonal elements are same static boolean checkDiagonal ( List < List < Integer >> mat int x int y ) { int n = mat . size () m = mat . get ( 0 ). size (); for ( int i = x + 1 j = y + 1 ; i < n && j < m ; i ++ j ++ ) { if ( ! mat . get ( i ). get ( j ). equals ( mat . get ( x ). get ( y ))) return false ; } return true ; } // Function to check whether given // matrix is toeplitz matrix or not static boolean isToeplitz ( List < List < Integer >> mat ) { int n = mat . size () m = mat . get ( 0 ). size (); // check each descending diagonal starting from // first row and first column of the matrix for ( int i = 0 ; i < m ; i ++ ) if ( ! checkDiagonal ( mat 0 i )) return false ; for ( int i = 0 ; i < n ; i ++ ) if ( ! checkDiagonal ( mat i 0 )) return false ; // if all diagonals are same return true return true ; } public static void main ( String [] args ) { List < List < Integer >> mat = Arrays . asList ( Arrays . asList ( 6 7 8 ) Arrays . asList ( 4 6 7 ) Arrays . asList ( 1 4 6 ) ); if ( isToeplitz ( mat )) { System . out . println ( 'Yes' ); } else { System . out . println ( 'No' ); } } }
Python # function to check if diagonal elements are same def checkDiagonal ( mat x y ): n m = len ( mat ) len ( mat [ 0 ]) i j = x + 1 y + 1 while i < n and j < m : if mat [ i ][ j ] != mat [ x ][ y ]: return False i += 1 j += 1 return True # Function to check whether given # matrix is toeplitz matrix or not def isToeplitz ( mat ): n m = len ( mat ) len ( mat [ 0 ]) # check each descending diagonal starting from # first row and first column of the matrix for i in range ( m ): if not checkDiagonal ( mat 0 i ): return False for i in range ( n ): if not checkDiagonal ( mat i 0 ): return False # if all diagonals are same return true return True mat = [ [ 6 7 8 ] [ 4 6 7 ] [ 1 4 6 ] ] if isToeplitz ( mat ): print ( 'Yes' ) else : print ( 'No' )
C# using System ; using System.Collections.Generic ; class GfG { // function to check if diagonal elements are same static bool checkDiagonal ( List < List < int >> mat int x int y ) { int n = mat . Count m = mat [ 0 ]. Count ; for ( int i = x + 1 j = y + 1 ; i < n && j < m ; i ++ j ++ ) { if ( mat [ i ][ j ] != mat [ x ][ y ]) return false ; } return true ; } // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz ( List < List < int >> mat ) { int n = mat . Count m = mat [ 0 ]. Count ; // check each descending diagonal starting from // first row and first column of the matrix for ( int i = 0 ; i < m ; i ++ ) if ( ! checkDiagonal ( mat 0 i )) return false ; for ( int i = 0 ; i < n ; i ++ ) if ( ! checkDiagonal ( mat i 0 )) return false ; // if all diagonals are same return true return true ; } static void Main () { var mat = new List < List < int >> { new List < int > { 6 7 8 } new List < int > { 4 6 7 } new List < int > { 1 4 6 } }; if ( isToeplitz ( mat )) { Console . WriteLine ( 'Yes' ); } else { Console . WriteLine ( 'No' ); } } }
JavaScript // function to check if diagonal elements are same function checkDiagonal ( mat x y ) { let n = mat . length m = mat [ 0 ]. length ; for ( let i = x + 1 j = y + 1 ; i < n && j < m ; i ++ j ++ ) { if ( mat [ i ][ j ] !== mat [ x ][ y ]) return false ; } return true ; } // Function to check whether given // matrix is toeplitz matrix or not function isToeplitz ( mat ) { let n = mat . length m = mat [ 0 ]. length ; // check each descending diagonal starting from // first row and first column of the matrix for ( let i = 0 ; i < m ; i ++ ) if ( ! checkDiagonal ( mat 0 i )) return false ; for ( let i = 0 ; i < n ; i ++ ) if ( ! checkDiagonal ( mat i 0 )) return false ; // if all diagonals are same return true return true ; } let mat = [ [ 6 7 8 ] [ 4 6 7 ] [ 1 4 6 ] ]; if ( isToeplitz ( mat )) { console . log ( 'Yes' ); } else { console . log ( 'No' ); }
Išvestis
Yes
[Numatomas požiūris – 2] – Tikrinimas įstrižai virš elemento – O(n * n) laikas ir O(1) erdvė
Idėja yra nuskaityti kiekvieną langelį nuo antrosios eilutės ir antrojo stulpelio, lyginant kiekvieną reikšmę su jos viršutiniame kairiajame kaimyne. Jei kuris nors elementas skiriasi nuo įstrižai virš jo esančio, pastebėjote Toeplitz savybės pažeidimą ir galite nedelsiant sustabdyti; jei pereisite per visą matricą be neatitikimo, kiekviena įstrižainė yra pastovi.
Atlikite toliau nurodytus veiksmus:
- Leiskite
n = mat.size()irm = mat[0].size(). - Pakartokite
inuo 1 ikin - 1ir per taijnuo 1 ikim - 1. - Jeigu
mat[i][j] != mat[i - 1][j - 1]bet kuriuo momentu grįžtifalse. - Patikrinus visas poras be neatitikimų, grįžta
true.
Žemiau pateikiama įgyvendinimas:
C++ #include using namespace std ; // Function to check whether given // matrix is toeplitz matrix or not bool isToeplitz ( vector < vector < int >> & mat ) { int n = mat . size () m = mat [ 0 ]. size (); // check diagonally above element of // each element in the matrix for ( int i = 1 ; i < n ; i ++ ) { for ( int j = 1 ; j < m ; j ++ ) { if ( mat [ i ][ j ] != mat [ i - 1 ][ j - 1 ]) return false ; } } // if all diagonals are same return true return true ; } int main () { vector < vector < int >> mat = { { 6 7 8 } { 4 6 7 } { 1 4 6 } }; if ( isToeplitz ( mat )) { cout < < 'Yes' ; } else { cout < < 'No' ; } return 0 ; }
Java import java.util.* ; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static boolean isToeplitz ( List < List < Integer >> mat ) { int n = mat . size () m = mat . get ( 0 ). size (); // check diagonally above element of // each element in the matrix for ( int i = 1 ; i < n ; i ++ ) { for ( int j = 1 ; j < m ; j ++ ) { if ( mat . get ( i ). get ( j ) != mat . get ( i - 1 ). get ( j - 1 )) return false ; } } // if all diagonals are same return true return true ; } public static void main ( String [] args ) { List < List < Integer >> mat = Arrays . asList ( Arrays . asList ( 6 7 8 ) Arrays . asList ( 4 6 7 ) Arrays . asList ( 1 4 6 ) ); if ( isToeplitz ( mat )) { System . out . println ( 'Yes' ); } else { System . out . println ( 'No' ); } } }
Python # Function to check whether given # matrix is toeplitz matrix or not def isToeplitz ( mat ): n m = len ( mat ) len ( mat [ 0 ]) # check diagonally above element of # each element in the matrix for i in range ( 1 n ): for j in range ( 1 m ): if mat [ i ][ j ] != mat [ i - 1 ][ j - 1 ]: return False # if all diagonals are same return true return True mat = [ [ 6 7 8 ] [ 4 6 7 ] [ 1 4 6 ] ] if isToeplitz ( mat ): print ( 'Yes' ) else : print ( 'No' )
C# using System ; using System.Collections.Generic ; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz ( List < List < int >> mat ) { int n = mat . Count m = mat [ 0 ]. Count ; // check diagonally above element of // each element in the matrix for ( int i = 1 ; i < n ; i ++ ) { for ( int j = 1 ; j < m ; j ++ ) { if ( mat [ i ][ j ] != mat [ i - 1 ][ j - 1 ]) return false ; } } // if all diagonals are same return true return true ; } static void Main () { var mat = new List < List < int >> { new List < int > { 6 7 8 } new List < int > { 4 6 7 } new List < int > { 1 4 6 } }; if ( isToeplitz ( mat )) { Console . WriteLine ( 'Yes' ); } else { Console . WriteLine ( 'No' ); } } }
JavaScript // Function to check whether given // matrix is toeplitz matrix or not function isToeplitz ( mat ) { let n = mat . length m = mat [ 0 ]. length ; // check diagonally above element of // each element in the matrix for ( let i = 1 ; i < n ; i ++ ) { for ( let j = 1 ; j < m ; j ++ ) { if ( mat [ i ][ j ] !== mat [ i - 1 ][ j - 1 ]) return false ; } } // if all diagonals are same return true return true ; } let mat = [ [ 6 7 8 ] [ 4 6 7 ] [ 1 4 6 ] ]; if ( isToeplitz ( mat )) { console . log ( 'Yes' ); } else { console . log ( 'No' ); }
Išvestis
Yes
[Alternatyvus metodas] – maišos naudojimas – O(n * n) laikas ir O(n) erdvė
Idėja yra priskirti unikalų identifikatorių kiekvienai apatinei įstrižainei (eilutės indeksas atėmus stulpelio indeksą) ir naudoti maišos žemėlapį, kad įrašytumėte pirmąją tos įstrižainės reikšmę. Nuskaitydami visą matricą, apskaičiuojate šį raktą kiekvienam langeliui ir patikrinate, ar jis atitinka išsaugotą reikšmę, arba išsaugokite, ar jis naujas. Vienintelis neatitikimas leidžia jums išgelbėti melagingus; kitaip pabaigoje padarysite teisingą išvadą.
Atlikite toliau nurodytus veiksmus:
- Nustatykite matricos matmenis (eilučių skaičių ir stulpelių skaičių) iš
mat. - Sukurkite tuščią hashmapą
mpsusieti kiekvieną įstrižainės raktą su jo reprezentacine verte. - Eikite per kiekvieną ląstelę
matpagal eilučių indeksąiir stulpelio indeksasj. - Kiekvienam langeliui suformuokite įstrižainės raktą atimdami
jiši. - Jeigu
mpjau turi šį raktą, palyginkite dabartinį elementą su išsaugota reikšme; jei jie skiriasi, nedelsiant grąžinkite klaidingą. - Jei raktas dar neįdėtas
mpįrašyti dabartinį elementą po tuo raktu. - Jei atliksite perėjimą be neatitikimų, grąžinkite teisingą.
Iliustracija:
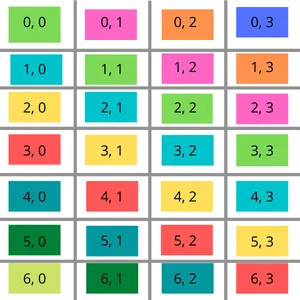
Žemiau pateikta diagrama geriau įsivaizduoja šią idėją. Apsvarstykite geltonos spalvos įstrižainę. Skirtumas tarp bet kurio šios įstrižainės indekso x reikšmės ir y vertės yra 2 (2-0 3-1 4-2 5-3). Tą patį galima pastebėti su visomis kūno įstrižainėmis.

Raudonos spalvos įstrižainės skirtumas yra 3. Žalios spalvos įstrižainės skirtumas yra 0. Oranžinės spalvos įstrižainės skirtumas yra -2 ir tt...
Žemiau pateikiama įgyvendinimas:
C++ #include using namespace std ; // Function to check whether given // matrix is toeplitz matrix or not bool isToeplitz ( vector < vector < int >> & mat ) { int n = mat . size () m = mat [ 0 ]. size (); // HashMap to store keyvalue pairs unordered_map < int int > mp ; for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < m ; j ++ ) { int key = i - j ; // If key value exists in the hashmap if ( mp [ key ]) { // check if the value is same // as the current element if ( mp [ key ] != mat [ i ][ j ]) return false ; } // Else we put keyvalue pair in hashmap else { mp [ i - j ] = mat [ i ][ j ]; } } } return true ; } int main () { vector < vector < int >> mat = { { 6 7 8 } { 4 6 7 } { 1 4 6 } }; if ( isToeplitz ( mat )) { cout < < 'Yes' ; } else { cout < < 'No' ; } return 0 ; }
Java // JAVA program to check whether given matrix // is a Toeplitz matrix or not import java.util.* ; class GFG { static boolean isToeplitz ( int [][] matrix ) { // row = number of rows // col = number of columns int row = matrix . length ; int col = matrix [ 0 ] . length ; // HashMap to store keyvalue pairs HashMap < Integer Integer > map = new HashMap < Integer Integer > (); for ( int i = 0 ; i < row ; i ++ ) { for ( int j = 0 ; j < col ; j ++ ) { int key = i - j ; // if key value exists in the hashmap if ( map . containsKey ( key )) { // we check whether the current value // stored in this key matches to element // at current index or not. If not // return false if ( map . get ( key ) != matrix [ i ][ j ] ) return false ; } // else we put keyvalue pair in hashmap else { map . put ( i - j matrix [ i ][ j ] ); } } } return true ; } // Driver Code public static void main ( String [] args ) { int [][] matrix = { { 12 23 - 32 } { - 20 12 23 } { 56 - 20 12 } { 38 56 - 20 } }; // Function call String result = ( isToeplitz ( matrix )) ? 'Yes' : 'No' ; System . out . println ( result ); } }
Python # Python3 program to check whether given matrix # is a Toeplitz matrix or not def isToeplitz ( matrix ): # row = number of rows # col = number of columns row = len ( matrix ) col = len ( matrix [ 0 ]) # dictionary to store keyvalue pairs map = {} for i in range ( row ): for j in range ( col ): key = i - j # if key value exists in the map if ( key in map ): # we check whether the current value stored # in this key matches to element at current # index or not. If not return false if ( map [ key ] != matrix [ i ][ j ]): return False # else we put keyvalue pair in map else : map [ key ] = matrix [ i ][ j ] return True # Driver Code if __name__ == '__main__' : matrix = [[ 12 23 - 32 ] [ - 20 12 23 ] [ 56 - 20 12 ] [ 38 56 - 20 ]] # Function call if ( isToeplitz ( matrix )): print ( 'Yes' ) else : print ( 'No' )
C# using System ; using System.Collections.Generic ; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz ( List < List < int >> mat ) { int n = mat . Count m = mat [ 0 ]. Count ; // HashMap to store keyvalue pairs Dictionary < int int > mp = new Dictionary < int int > (); for ( int i = 0 ; i < n ; i ++ ) { for ( int j = 0 ; j < m ; j ++ ) { int key = i - j ; // If key value exists in the hashmap if ( mp . ContainsKey ( key )) { // check if the value is same // as the current element if ( mp [ key ] != mat [ i ][ j ]) return false ; } // Else we put keyvalue pair in hashmap else { mp [ i - j ] = mat [ i ][ j ]; } } } return true ; } static void Main () { var mat = new List < List < int >> { new List < int > { 6 7 8 } new List < int > { 4 6 7 } new List < int > { 1 4 6 } }; if ( isToeplitz ( mat )) { Console . WriteLine ( 'Yes' ); } else { Console . WriteLine ( 'No' ); } } }
JavaScript // Function to check whether given // matrix is toeplitz matrix or not function isToeplitz ( mat ) { let n = mat . length m = mat [ 0 ]. length ; // HashMap to store keyvalue pairs const mp = new Map (); for ( let i = 0 ; i < n ; i ++ ) { for ( let j = 0 ; j < m ; j ++ ) { let key = i - j ; // If key value exists in the hashmap if ( mp . has ( key )) { // check if the value is same // as the current element if ( mp . get ( key ) !== mat [ i ][ j ]) return false ; } // Else we put keyvalue pair in hashmap else { mp . set ( i - j mat [ i ][ j ]); } } } return true ; } let mat = [ [ 6 7 8 ] [ 4 6 7 ] [ 1 4 6 ] ]; if ( isToeplitz ( mat )) { console . log ( 'Yes' ); } else { console . log ( 'No' ); }
Išvestis
Yes