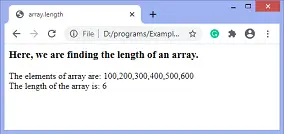
Dekoderis

Kombinuota grandinė, pakeičianti dvejetainę informaciją į 2 N išvesties linijos yra žinomos kaip Dekoderiai. Dvejetainė informacija perduodama N įvesties eilučių forma. Išvesties linijos apibrėžia 2 N -bitinis dvejetainės informacijos kodas. Paprastais žodžiais tariant, Dekoderis atlieka atvirkštinę operaciją Encoder . Dėl paprastumo vienu metu aktyvuojama tik viena įvesties eilutė. Pagamintas 2 N -bitų išvesties kodas yra lygiavertis dvejetainei informacijai.

Yra įvairių tipų dekoderių, kurie yra tokie:
2–4 eilučių dekoderis:
2–4 eilučių dekoderyje iš viso yra trys įėjimai, ty A 0 , ir A 1 ir E bei keturi išėjimai, ty Y 0 , IR 1 , IR 2 , ir Y 3 . Kiekvienam įėjimų deriniui, kai įgalinimo 'E' yra nustatytas į 1, vienas iš šių keturių išėjimų bus 1. Toliau pateikiamos 2–4 eilučių dekoderio blokinės diagramos ir tiesos lentelė.
Blokinė diagrama:

Tiesos lentelė:

Loginė terminų Y0, Y0, Y2 ir Y3 išraiška yra tokia:
IR 3 =E.A 1 .A 0
IR 2 =E.A 1 .A 0 “
IR 1 =E.A 1 „.A 0
Y0=E.A 1 „.A 0 “
Aukščiau pateiktų išraiškų loginė grandinė pateikta žemiau:

3–8 eilučių dekoderis:
3–8 eilučių dekoderis taip pat žinomas kaip Dvejetainis į aštuntainį dekoderis . 3–8 eilučių dekoderyje iš viso yra aštuoni išėjimai, ty Y 0 , IR 1 , IR 2 , IR 3 , IR 4 , IR 5 , IR 6 , ir Y 7 ir trys išėjimai, ty A 0 , A1 ir A 2 . Ši grandinė turi įjungimo įvestį „E“. Kaip ir 2–4 eilučių dekoderis, kai įgalinimas „E“ yra nustatytas į 1, vienas iš šių keturių išėjimų bus 1. Toliau pateikiama 3–8 eilučių kodavimo bloko schema ir tiesos lentelė.
Blokinė diagrama:

Tiesos lentelė:

Loginė termino Y išraiška 0 , IR 1 , IR 2 , IR 3 , IR 4 , IR 5 , IR 6 , ir Y 7 yra taip:
IR 0 =A 0 „.A 1 „.A 2 “
IR 1 =A 0 .A 1 „.A 2 “
IR 2 =A 0 „.A 1 .A 2 “
IR 3 =A 0 .A 1 .A 2 “
IR 4 =A 0 „.A 1 „.A 2
IR 5 =A 0 .A 1 „.A 2
IR 6 =A 0 „.A 1 .A 2
IR 7 =A 0 .A 1 .A 2
Aukščiau pateiktų išraiškų loginė grandinė pateikta žemiau:

4–16 eilučių dekoderis
4–16 eilučių dekoderyje iš viso yra 16 išėjimų, t. y. Y 0 , IR 1 , IR 2 ,……, IR 16 ir keturios įvestys, ty A 0 , A1, A 2 , ir A 3 . 3–16 eilučių dekoderis gali būti sukonstruotas naudojant 2–4 dekoderius arba 3–8 dekoderius. Norint rasti reikiamą žemesnės eilės dekoderių skaičių, naudojama tokia formulė.
Reikalingas žemesnės eilės dekoderių skaičius=m 2 /m 1
m 1 = 8
m 2 = 16
Reikalingas 3–8 dekoderių skaičius=  =2
=2
Blokinė diagrama:

Tiesos lentelė:

Loginė termino A0, A1, A2,…, A15 išraiška yra tokia:
IR 0 =A 0 „.A 1 „.A 2 „.A 3 “
IR 1 =A 0 „.A 1 „.A 2 „.A 3
IR 2 =A 0 „.A 1 „.A 2 .A 3 “
IR 3 =A 0 „.A 1 „.A 2 .A 3
IR 4 =A 0 „.A 1 .A 2 „.A 3 “
IR 5 =A 0 „.A 1 .A 2 „.A 3
IR 6 =A 0 „.A 1 .A 2 .A 3 “
IR 7 =A 0 „.A 1 .A 2 .A 3
IR 8 =A 0 .A 1 „.A 2 „.A 3 “
IR 9 =A 0 .A 1 „.A 2 „.A 3
IR 10 =A 0 .A 1 „.A 2 .A 3 “
IR vienuolika =A 0 .A 1 „.A 2 .A 3
IR 12 =A 0 .A 1 .A 2 „.A 3 “
IR 13 =A 0 .A 1 .A 2 „.A 3
IR 14 =A 0 .A 1 .A 2 .A 3 “
IR penkiolika =A 0 .A 1 .A 2 „.A 3
Aukščiau pateiktų išraiškų loginė grandinė pateikta žemiau: