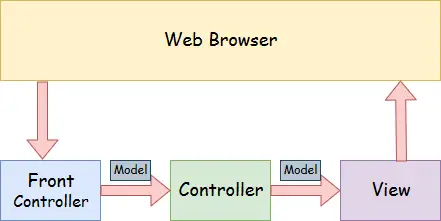
a ² – b ² formulėje Algebra yra pagrindinė matematikos formulė, naudojama įvairiems algebriniams uždaviniams spręsti. a ² – b ² formulė taip pat vadinama kvadratinės formulės skirtumu, nes ši formulė padeda rasti skirtumą tarp dviejų kvadratų iš tikrųjų neskaičiuojant kvadratų. Žemiau pateiktame paveikslėlyje parodyta a formulė ² – b ²

Šiame straipsnyje mes sužinosime a ² – b ² formulė, a ² – b ² tapatybę, pavyzdžius ir kitus išsamiai.

Turinys

• Kas yra a2 – b2 formulė?
• Kvadratų skirtumo formulė
• a2 – b2 kvadratinės formulės įrodymas
• (a + b)2 ir (a – b)2 formulė
• a2 – b2 Tapatybė

Kas yra a ² – b ² Formulė?

a ² – b ² algebros formulė yra pagrindinė algebrinių problemų sprendimo formulė. Jis taip pat naudojamas trigonometrinėms, diferencialinėms ir kitoms problemoms spręsti. Ši formulė mums sako, kad skirtumas tarp dviejų kvadratinių skaičių yra lygus dviejų skaičių sumos ir skirtumo sandaugai, t.y.

a ² – b ² = (a + b).(a – b)

a ² – b ² Formulės apibrėžimas

Formulė a ² – b ² leidžia nustatyti dispersiją tarp dviejų skaičių kvadratų, neskaičiuojant tikrosios kvadrato reikšmių. Išraiška a ² – b ² formulė yra tokia: a ² – b ² = (a + b).(a – b)

Kvadratų skirtumo formulė

Dviejų kvadratų skirtumas apskaičiuojamas naudojant standartinę algebrinę tapatybę a ² – b ² . Pavyzdžiui, mums pateikiami du kintamieji a ir b, tada jų kvadratų skirtumas apskaičiuojamas naudojant formulę, a ² – b ² = (a+b).(a–b)

Iš esmės kvadratų skirtumo formulė sako, kad bet kuriems dviem algebriniams kintamiesiems a ir b išraiška a ² – b ² yra lygus kintamųjų sumos ir skirtumo sandaugai. Ši tapatybė plačiai naudojama sudėtingoms algebrinėms išraiškoms supaprastinti.

a ² – b ² Kvadratinės formulės įrodymas

a ² – b ² tapatybę galima įrodyti supaprastinant tapatybės RHS. A ² – b ² formulė pateikiama kaip

a ² – b ² = (a – b)(a + b)

Ši formulė įrodyta kaip

RHS = (a+b) (a–b)

⇒ RHS = a (a–b) + b (a–b)

⇒ RHS = a ² – ab + ba – b ²

⇒ RHS = a ² – ab + ab – b ²

⇒ RHS = a ² – b ²

⇒ RHS = LHS

Taigi įrodyta.

a ² + b ² Formulė

A ² + b ² formulė yra algebrinė formulė, naudojama dviejų skaičių kvadratų sumai rasti. Kvadratinės formulės suma pateikiama taip,

a ² + b ² = (a + b) ² – 2ab

A ² + b ² formulė naudojama įvairiems algebriniams uždaviniams spręsti. Toliau pridedamos įvairios kitos svarbios algebrinės formulės,

(a + b) ² ir (a–b) ² Formulė

(a + b) ² formulė pateikiama kaip

(a + b) ² = a ² + b ² + 2ab

(a–b) ² formulė pateikiama kaip

(a–b) ² = a ² + b ² – 2ab

a ² – b ² Tapatybė

a ² – b ² tapatybė yra viena iš algebrinės tapatybės kuris naudojamas dviejų skaičių kvadratų skirtumui rasti. Ši tapatybė gali būti naudojama įvairiai ir pateikiama kaip

a ² – b ² = (a – b).(a + b)

Skaityti daugiau,

• Algebros formulė
• Pagrindinė matematikos formulė
• Algebrinė išraiška

Pavyzdžiai ant a ² – b ² Formulė

1 pavyzdys: supaprastinkite x ² – 16

Sprendimas:

= x ² – 16

= x ² – 4 ²

Mes tai žinome, a ² – b ² = (a+b) (a–b)

Atsižvelgiant į

• a = x
• b = 4

= (x + 4) (x – 4)

2 pavyzdys: Supaprastinkite 9 m ² – 144

Sprendimas:

= 9 m ² – 144

= (3 m.) ² – (12) ²

Mes tai žinome, a ² – b ² = (a+b)(a–b)

Atsižvelgiant į

• a = 3 m
• b = 12

= (3 m. + 12) (3 m. – 12)

3 pavyzdys: supaprastinkite (3x + 2) ² – (3x – 2) ²

Sprendimas:

Mes tai žinome,

a ² – b ² = (a+b)(a–b)

Atsižvelgiant į

• a = 3x + 2
• b = 3x – 2

(3x + 2) ² – (3x – 2) ²

= (3x + 2 + 3x - 2) (3x + 2 - (3x - 2))

= 6x (3x + 2 – 3x + 2)

= 6x (4)

= 24x

4 pavyzdys: supaprastinkite ir ² – 100

Sprendimas:

= ir ² – 100

= ir ² – (10) ²

Mes tai žinome,

a ² – b ² = (a+b)(a–b)

Atsižvelgiant į

• a = ir
• b = 10

= (y + 10) (y – 10)

5 pavyzdys: įvertinkite (x + 6) (x - 6)

Sprendimas:

Mes tai žinome,

(a+b) (a–b) = a ² – b ²

Atsižvelgiant į

• a = x
• b = 6

(x + 6) (x – 6)

= x ² – 6 ²

= x ² – 36

6 pavyzdys: įvertinkite (y + 13) (y - 13)

Sprendimas:

Mes tai žinome,

(a+b) (a–b) = a ² – b ²

Atsižvelgiant į

• a = ir
• b = 13

(y + 13). (y – 13)

= ir ² – (13) ²

= ir ² – 169

7 pavyzdys: įvertinkite (x + y + z). (x + y – z)

Sprendimas:

Mes tai žinome,

(a+b) (a–b) = a ² – b ²

Atsižvelgiant į

• a = x + y
• b = z

(x + y + z) (x + y – z)

= (x + y) ² - Su ²

= x ² + ir ² + 2xy – z ²

(a ² – b ² ) Formulė – Užduotis

Q1. Supaprastinkite 15 ² – 14 ² naudojant a ² – b ² tapatybę.

Q2. Supaprastinkite 11 ² – 7 ² naudojant a ² – b ² tapatybę.

Q3. Išspręskite 23 ² – 9 ² naudojant a ² – b ² tapatybę.

4 klausimas. Išspręskite 9 ² – 7 ² naudojant a ² – b ² tapatybę.

a ² – b ² Formulė – DUK

1. Kas yra a ² − b ² ?

a ² – b ² formulė yra formulė, kuri naudojama norint rasti skirtumą tarp dviejų kvadratų, faktiškai nerandant kvadrato. A ² – b ² formulė yra,

a ² – b ² = (a + b) (a – b)

2. Kas yra a dėsnis ² b ² Formulė?

A dėsnis ² b ² formulės yra,

• a ² – b ² = (a + b) (a – b)
• a ² + b ² = (a + b) ² – 2ab

3. Kas yra a ² b ² Formulė naudojama?

a ² b ² formulės naudojamos įvairiems algebriniams uždaviniams spręsti, jos taip pat naudojamos trigonometriniams, skaičiavimo, integravimo uždaviniams supaprastinti.

4. Kas yra a ² b ² Formulė?

Yra du a ² b ² formulės, kurios yra, a ² + b ² , ir a ² – b ² išplėtimo formulė a ² b ² formulės pateikiamos taip,

• a ² – b ² = (a + b) (a – b)
• a ² + b ² = (a + b) ² – 2ab

5. Kada yra a ² – b ² Formulė naudojama?

a ² – b ² formulė naudojama norint rasti skirtumą tarp dviejų skaičių kvadratų, iš tikrųjų nerandant kvadratų. Ši formulė taip pat naudojama sprendžiant įvairius algebrinius, trigonometrinius ir kitus uždavinius.