Programmation linéaire
Programmation linéaire est un concept mathématique utilisé pour trouver la solution optimale de la fonction linéaire. Cette méthode utilise des hypothèses simples pour optimiser la fonction donnée. La programmation linéaire a une énorme application dans le monde réel et est utilisée pour résoudre divers types de problèmes.
La programmation linéaire est utilisée dans diverses industries telles que les industries maritimes, les industries manufacturières, les industries des transports, les télécommunications et autres.
Le terme programmation linéaire se compose de deux mots linéaire et programmation, le mot linéaire raconte la relation entre différents types de variables de degré un utilisées dans un problème et le mot programmation nous indique la procédure étape par étape pour résoudre ces problèmes.
Dans cet article, nous découvrirons en détail la programmation linéaire, ses exemples, ses formules et d’autres concepts.
Table des matières
- Qu’est-ce que la programmation linéaire ?
- Composants de la programmation linéaire
- Exemples de programmation linéaire
- Problèmes de programmation linéaire
- Types de problèmes de programmation linéaire
- Formule de programmation linéaire
- Comment résoudre les problèmes de programmation linéaire ?
- Méthodes de programmation linéaire
- Méthode Simplex de programmation linéaire
- Méthode graphique de programmation linéaire
- Applications de programmation linéaire
- Importance de la programmation linéaire
- Applications récentes de la programmation linéaire
- Programmation linéaire en recherche opérationnelle
- Méthode simplexe
Qu’est-ce que la programmation linéaire ?
Programmation linéaire ou Optimisation linéaire est une technique qui nous aide à trouver la solution optimale pour un problème donné, une solution optimale est une solution qui est le meilleur résultat possible pour un problème particulier donné.
En termes simples, c’est la méthode pour découvrir comment faire quelque chose de la meilleure façon possible. Avec des ressources limitées, vous devez utiliser les ressources de manière optimale et obtenir le meilleur résultat possible dans un objectif particulier tel que le moindre coût, la marge la plus élevée ou le moins de temps.
La situation qui nécessite une recherche des meilleures valeurs des variables soumises à certaines contraintes est celle où l'on utilise des problèmes de programmation linéaire. Ces situations ne peuvent pas être traitées par les calculs et techniques numériques habituels.
Définition de la programmation linéaire
La programmation linéaire est la technique utilisée pour optimiser un scénario particulier. L'utilisation de la programmation linéaire nous offre le meilleur résultat possible dans une situation donnée. Il utilise toutes les ressources disponibles de manière à produire le résultat optimal.
Composants de la programmation linéaire
Les composants de base d'un problème de programmation linéaire (LP) sont :
- Variables de décision : Variables que vous souhaitez déterminer pour obtenir la solution optimale.
- Fonction objectif : M équation athématique qui représente l'objectif que vous souhaitez atteindre
- Contraintes: Limitations ou restrictions que vos variables de décision doivent suivre.
- Restrictions de non-négativité : Dans certaines scénarios du monde réel, les variables de décision ne peuvent pas être négatives
Caractéristiques supplémentaires de la programmation linéaire
- Finitude : Le nombre de variables de décision et de contraintes dans un problème LP est fini.
- Linéarité : La fonction objectif et toutes les contraintes doivent être des fonctions linéaires des variables de décision . Cela signifie que le degré des variables doit être un.
Exemples de programmation linéaire
Nous pouvons comprendre les situations dans lesquelles la programmation linéaire est appliquée à l'aide de l'exemple discuté ci-dessous,
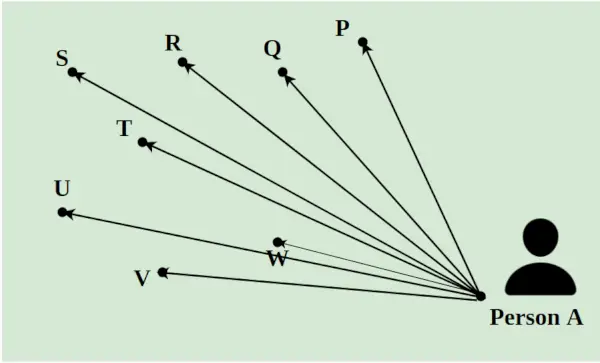
Supposons qu’un livreur doive livrer 8 colis par jour aux différents endroits d’une ville. Il doit récupérer tous les paquets de A et les livrer aux points P, Q, R, S, T, U, V et W. La distance entre eux est indiquée à l'aide des lignes comme indiqué dans l'image ci-dessous. Le chemin le plus court suivi par le livreur est calculé selon le concept de Programmation Linéaire.

Problèmes de programmation linéaire
Problèmes de programmation linéaire (LPP) impliquent d’optimiser une fonction linéaire pour trouver la solution de valeur optimale pour la fonction. La valeur optimale peut être soit la valeur maximale, soit la valeur minimale.
En LPP, les fonctions linéaires sont appelées fonctions objectives. Une fonction objectif peut avoir plusieurs variables, qui sont soumises à des conditions et doivent satisfaire aux contraintes linéaires .
Types de problèmes de programmation linéaire
Il existe de nombreux problèmes de programmation linéaire (LPP) différents, mais nous traiterons de trois problèmes majeurs de programmation linéaire dans cet article.
Problèmes de fabrication
Les problèmes de fabrication sont un problème qui concerne le nombre d'unités qui doivent être produites ou vendues pour maximiser les profits lorsque chaque produit nécessite une main d'œuvre, des heures de machine et des matières premières fixes.
Problèmes de régime
Il est utilisé pour calculer le nombre de différents types de constituants à inclure dans le régime alimentaire pour obtenir le coût minimum, en fonction de la disponibilité des aliments et de leurs prix.
Problèmes de transport
Il est utilisé pour déterminer le calendrier de transport afin de trouver le moyen le moins cher de transporter un produit depuis des usines/usines situées à différents endroits vers différents marchés.
Formule de programmation linéaire
Un problème de programmation linéaire consiste à,
- Variables de décision
- Fonction objectif
- Contraintes
- Restrictions non négatives
Variables de décision sont les variables x et y, qui déterminent le résultat du problème de programmation linéaire et représentent la solution finale.
Le fonction objectif , généralement représentée par Z, est la fonction linéaire qui doit être optimisée en fonction de la condition donnée pour obtenir la solution finale.
Le restrictions imposées aux variables de décision qui limitent leurs valeurs sont appelées contraintes.
Maintenant, la formule générale d’un problème de programmation linéaire est :
Fonction objectif : Z = hache + par
Contraintes: cx + dy ≥ e, px + qy ≤ r
Restrictions non négatives : x ≥ 0, y ≥ 0
Dans la condition ci-dessus, x et y sont les variables de décision.
Comment résoudre les problèmes de programmation linéaire ?
Avant de résoudre les problèmes de programmation linéaire, nous devons d’abord formuler les problèmes en fonction des paramètres standards. Les étapes pour résoudre les problèmes de programmation linéaire sont les suivantes :
Étape 1: Marquez les variables de décision dans le problème.
Étape 2: Construisez la fonction objectif du problème et vérifiez si la fonction doit être minimisée ou maximisée.
Étape 3: Notez toutes les contraintes des problèmes linéaires.
Étape 4: Assurer des restrictions non négatives des variables de décision.
Étape 5 : Résolvez maintenant le problème de programmation linéaire en utilisant n'importe quelle méthode, généralement nous utilisons la méthode simplex ou graphique.
Méthodes de programmation linéaire
Nous utilisons diverses méthodes pour résoudre des problèmes de programmation linéaire. Les deux méthodes les plus couramment utilisées sont,
- Méthode simplexe
- Méthode graphique
Découvrons ces deux méthodes en détail dans cet article,
Méthode Simplex de programmation linéaire
L’une des méthodes les plus courantes pour résoudre le problème de programmation linéaire est la méthode du simplexe. Dans cette méthode, nous répétons une condition spécifique « n » plusieurs fois jusqu’à ce qu’une solution optimale soit obtenue.
Les étapes nécessaires pour résoudre des problèmes de programmation linéaire à l'aide de la méthode du simplexe sont les suivantes :
Étape 1: Formuler les problèmes de programmation linéaire en fonction des contraintes données.
Étape 2: Convertissez toutes les inégalités données en équations ou égalités des problèmes de programmation linéaire en ajoutant la variable slack à chaque inégalité lorsque cela est nécessaire.
Étape 3: Construisez la table simplex initiale. En représentant chaque équation de contrainte dans une ligne et en écrivant la fonction objectif dans la ligne du bas. La table ainsi obtenue est appelée table Simplex.
Étape 4: Identifiez l'entrée négative la plus élevée dans la ligne du bas. La colonne de l'élément avec l'entrée négative la plus élevée est appelée la colonne pivot.
Étape 5 : Divisez les entrées de la colonne la plus à droite avec les entrées de la colonne pivot respective, à l'exclusion des entrées de la ligne la plus basse. Désormais, la ligne contenant le moins d’entrées est appelée ligne pivot. L'élément pivot est obtenu par l'intersection de la ligne pivot et de la colonne pivot.
Étape 6 : En utilisant l'opération matricielle et à l'aide de l'élément pivot, faites en sorte que toutes les entrées de la colonne pivot soient nulles.
Étape 7 : Vérifiez les entrées non négatives dans la ligne du bas. S'il n'y a pas d'entrées négatives dans la ligne du bas, terminez le processus, sinon recommencez le processus à partir de l'étape 4.
Étape 8 : Le tableau simplex final ainsi obtenu donne la solution à notre problème.
Méthode graphique de programmation linéaire
La méthode graphique est une autre méthode que la méthode Simplex qui est utilisée pour résoudre des problèmes de programmation linéaire. Comme son nom l'indique, cette méthode utilise des graphiques pour résoudre les problèmes de programmation linéaire donnés. C’est la meilleure méthode pour résoudre des problèmes de programmation linéaire et nécessite moins d’efforts que la méthode simplexe.
En utilisant cette méthode, nous traçons toutes les inégalités soumises à des contraintes dans les problèmes de programmation linéaire donnés. Dès que toutes les inégalités du LPP donné sont tracées sur le graphe XY, la région commune de toutes les inégalités donne la solution optimale. Tous les points d'angle de la région réalisable sont calculés et la valeur de la fonction objectif en tous ces points est calculée, puis en comparant ces valeurs, nous obtenons la solution optimale du LPP.
Exemple : Trouver la valeur maximale et minimale de z = 6x + 9y lorsque les conditions de contrainte sont,
- 2x + 3 ans ≤ 12
- x et y ≥ 0
- x + y ≤ 5
Solution:
Étape 1 : Convertissez d’abord les inéquations en équations normales. Les équations seront donc 2x+3y = 0, x = 0, y = 0 et x + y = 5.
Étape 2 : Trouvez les points auxquels 2x + 3y et x + y = 5 coupent l'axe des x et l'axe des y. Pour trouver le point d'intersection de l'axe des x, mettez y = 0 dans l'équation respective et trouvez le point. De même, pour les points d'intersection de l'axe y, mettez x = 0 dans l'équation respective.
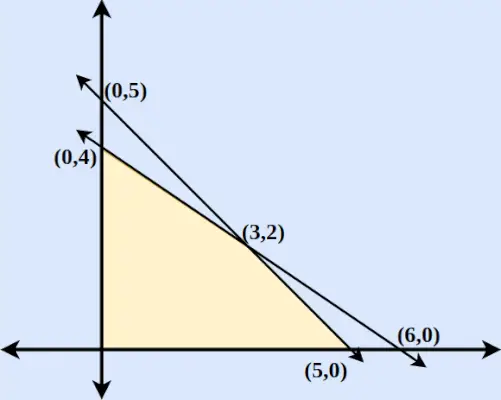
Étape 3 : Tracez les deux lignes coupant l'axe des x et l'axe des y. On constate que les deux axes se coupent en (3,2).
Étape 4 : Pour x ≥ 0 et y ≥ 0, nous constatons que les deux inéquations sont suivies. Par conséquent, la région comprendra une région délimitée par deux axes et les deux lignes incluant l'origine. La région tracée est illustrée ci-dessous dans la figure.
Étape 5 : Trouvez Z pour chaque point et maxima et minima.
Coordonnées Z = 6x + 9a (0,5) Z = 45 (0,4) Z = 36 (5.0) Z = 30 (6.0) Z = 36 (3.2) Z = 36 Par conséquent, nous constatons que Z = 6x + 9y est maximum en (0,5) et minimum en (5,0).
Applications de programmation linéaire
La programmation linéaire a des applications dans divers domaines. Il permet de trouver le coût minimum d'un processus lorsque toutes les contraintes du problème sont données. Il est utilisé pour optimiser le coût de transport du véhicule, etc. Diverses applications de la programmation linéaire sont
Industries de l'ingénierie
Les industries d'ingénierie utilisent la programmation linéaire pour résoudre des problèmes de conception et de fabrication et pour obtenir le rendement maximum d'une condition donnée.
Industries manufacturières
Les industries manufacturières utilisent la programmation linéaire pour maximiser les profits des entreprises et réduire les coûts de fabrication.
Secteurs de l'énergie
Les entreprises énergétiques utilisent la programmation linéaire pour optimiser leur production.
Industries des transports
La programmation linéaire est également utilisée dans les industries du transport pour trouver le chemin permettant de minimiser le coût du transport.
Importance de la programmation linéaire
La programmation linéaire revêt une importance capitale dans diverses industries : elle maximise la valeur de sortie tout en minimisant les valeurs d'entrée en fonction de diverses contraintes.
LP est très applicable lorsque nous avons plusieurs conditions lors de la résolution d'un problème et que nous devons optimiser le résultat du problème, c'est-à-dire que nous devons trouver la valeur minimale ou maximale en fonction d'une condition donnée.
En savoir plus,
- Inégalités linéaires
- Solution algébrique des inégalités linéaires
Problèmes de programmation linéaire
Problème 1 : Une entreprise fabrique et vend deux types de produits et le coût de production de chaque unité a et b est respectivement de 200 et 150 roupies. Chaque unité de produit génère un bénéfice de 20 roupies et chaque unité de produit b génère un bénéfice de 15 roupies à la vente. . L'entreprise estime que la demande mensuelle de A et B sera au maximum de l'unité récoltée dans tout le budget de production pour le mois fixé à 50 000 roupies. Combien d'unités l'entreprise doit-elle fabriquer pour tirer un profit maximum de ses ventes mensuelles d'un et B?
Solution:
Soit x = nombre d'unités de type A
y = Nombre d'unités de type B
Maximiser Z = 40x + 50y
Sous réserve des contraintes
3x + y ≤ 9
x + 2a ≤ 8
et x, y ≥ 0
Considérez l'équation,
3x + y = 9
x = 3
y = 0
et x + 2y = 8
x = 8
y = 0
Maintenant, nous pouvons déterminer la valeur maximale de Z en évaluant la valeur de Z aux quatre points (sommets) indiqués ci-dessous.
Sommets
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Bénéfice maximum, Z = Rs. 230
∴ Le nombre d'unités de type A est de 2 et le nombre d'unités de type B est de 3.
Problème 2 : Maximiser Z = 3x + 4y.
Sous réserve de contraintes , x + y ≤ 450, 2x + y ≤ 600 et x, y ≤ 0.
Solution:
Nous avons à partir du donné
Contraintes (1)
X + Oui = 450
Mettre x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Mettre y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Depuis, Contraintes (2)
2x + y = 600
Mettre x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Mettre y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Maintenant, nous avons les coordonnées des points Z = 3x + 4y
| Sommets | Z = 3x + 4a |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1 800 |
Par conséquent, la solution optimale maximale Z = 1800 aux coordonnées x = 0 et y = 450. Le graphique est donné ci-dessous.

Applications récentes de la programmation linéaire
La programmation linéaire, une technique mathématique puissante, est utilisée pour résoudre des problèmes d'optimisation dans diverses industries. Voici quelques applications modernes :
- Optimisation de la chaîne d'approvisionnement : La programmation linéaire aide les entreprises à minimiser les coûts et à maximiser l'efficacité de leurs chaînes d'approvisionnement. Il est utilisé pour déterminer les itinéraires de transport, les opérations d’entrepôt et les stratégies de gestion des stocks les plus rentables.
- Gestion de l'énergie : Dans le secteur de l'énergie, la programmation linéaire est utilisée pour optimiser le mix de méthodes de production d'énergie. Cela implique d’équilibrer les sources d’énergie traditionnelles avec des sources renouvelables afin de réduire les coûts et l’impact environnemental tout en répondant à la demande.
- Conception de réseaux de télécommunications : La programmation linéaire aide à concevoir des réseaux de télécommunications efficaces. Il aide à allouer la bande passante, à concevoir des configurations de réseau et à optimiser le flux de données pour garantir une communication à haut débit à moindre coût.
- Planification financière : Les entreprises et les analystes financiers utilisent la programmation linéaire pour l'optimisation de portefeuille, la gestion des risques et la budgétisation des investissements. Il aide à prendre des décisions d’investissement qui maximisent les rendements tout en minimisant les risques.
- Logistique des soins de santé : Dans le domaine de la santé, la programmation linéaire est appliquée pour optimiser l'allocation des ressources, telles que les lits d'hôpitaux, le personnel médical et les équipements. C’est crucial pour améliorer les soins aux patients, réduire les temps d’attente et gérer efficacement les coûts.
- Optimisation du processus de fabrication : La programmation linéaire est utilisée pour déterminer les niveaux de production optimaux pour plusieurs produits au sein d'une installation de fabrication, en tenant compte des contraintes telles que la main-d'œuvre, les matériaux et la disponibilité des machines.
- Planification agricole : Les agriculteurs et les planificateurs agricoles utilisent la programmation linéaire pour décider de la sélection des cultures, de l'utilisation des terres et de l'allocation des ressources afin de maximiser les rendements et les profits tout en préservant les ressources.
- Planification des équipages des compagnies aériennes : Les compagnies aériennes utilisent une programmation linéaire pour planifier efficacement les équipages, garantissant ainsi que les vols sont dotés d'un personnel conforme à la réglementation et minimisant les coûts opérationnels.
Ces applications démontrent la polyvalence et la puissance de la programmation linéaire pour résoudre des problèmes d’optimisation complexes dans divers secteurs, démontrant ainsi sa pertinence dans le monde actuel axé sur les données.
Programmation linéaire en recherche opérationnelle
- Outil de base : La programmation linéaire est un outil fondamental en recherche opérationnelle pour optimiser les ressources.
- Prise de décision : Aide à prendre les meilleures décisions concernant l'allocation des ressources, la maximisation des profits ou la minimisation des coûts.
- Applications étendues : Utilisé dans divers domaines tels que la logistique, la fabrication, la finance et la santé pour résoudre des problèmes complexes.
- Modélisation de problèmes du monde réel : Transforme les problèmes du monde réel en modèles mathématiques pour trouver les solutions les plus efficaces.
Méthode simplexe
- Algorithme d'optimisation : La méthode Simplex est un algorithme puissant utilisé en programmation linéaire pour trouver la solution optimale aux inégalités linéaires.
- Approche étape par étape : Il se déplace de manière itérative vers la meilleure solution en parcourant les bords de la région réalisable définie par des contraintes.
- Efficacité : Connu pour son efficacité dans la résolution de problèmes de programmation linéaire à grande échelle.
- Polyvalence : Applicable dans divers domaines tels que la planification diététique, les flux de réseau, la planification de la production, etc., démontrant sa polyvalence.
Programmation linéaire – FAQ
Qu’est-ce que la programmation linéaire ?
La programmation linéaire est un concept mathématique utilisé pour optimiser un problème linéaire donné comportant diverses contraintes. En utilisant la programmation linéaire, nous obtenons le résultat optimal du problème donné
Que sont les problèmes de programmation linéaire ?
Les problèmes de programmation linéaire (LPP) sont les problèmes qui donnent la solution optimale aux conditions données.
Qu’est-ce que la formule de programmation linéaire ?
Les formules générales de programmation linéaire sont,
- Fonction objectif : Z = hache + par
- Contraintes : px + qy ≤ r, sx + ty ≤ u
- Restrictions non négatives : x ≥ 0, y ≥ 0
Quels sont les différents types de programmation linéaire ?
Différents types de méthodes de programmation linéaire sont,
- Programmation linéaire par méthode Simplex
- Programmation linéaire par méthode R
- Programmation linéaire par méthode graphique
Quelles sont les exigences de la programmation linéaire ?
Diverses exigences des problèmes de programmation linéaire sont,
- Linéarité
- Fonction objectif
- Contraintes
- Non-négativité
Quels sont les avantages de la programmation linéaire ?
Les divers avantages de la programmation linéaire sont les suivants :
- Il fournit la solution optimale à tout problème linéaire donné.
- Il est facile à utiliser et donne toujours des résultats cohérents
- Cela permet de maximiser les profits et de réduire le coût des intrants.