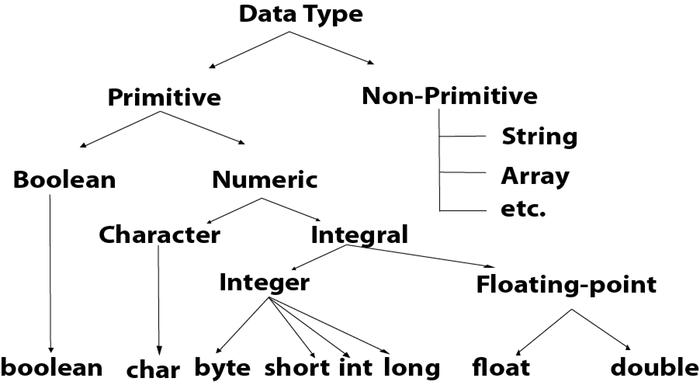
이진 트리의 각 수준의 극단 노드를 교대로 인쇄합니다.

GfG Practice에서 사용해 보세요.  #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; }
산출
 #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; } 각 레벨의 맨 끝 모서리에 대한 이진 트리 인쇄 노드가 있지만 순서는 교대로 지정됩니다.
예:

For above tree the output can be 1 2 7 8 31 - print rightmost node of 1st level - print leftmost node of 2nd level - print rightmost node of 3rd level - print leftmost node of 4th level - print rightmost node of 5th level OR 1 3 4 15 16 - print leftmost node of 1st level - print rightmost node of 2nd level - print leftmost node of 3rd level - print rightmost node of 4th level - print leftmost node of 5th levelRecommended Practice 교대로 배열된 극한 노드 시도해 보세요!
아이디어는 레벨별로 트리 레벨을 탐색하는 것입니다. 각 레벨에 대해 우리는 노드 수를 계산하고 부울 플래그 값을 기반으로 가장 왼쪽 또는 가장 오른쪽 노드를 인쇄합니다. 현재 레벨의 모든 노드를 대기열에서 제외하고 다음 레벨의 모든 노드를 대기열에 추가하며 레벨을 전환할 때 부울 플래그 값을 반전시킵니다.
아래는 위의 아이디어를 구현한 것입니다.
C++ /* C++ program to print nodes of extreme corners of each level in alternate order */ #include using namespace std ; /* A binary tree node has data pointer to left child and a pointer to right child */ struct Node { int data ; Node * left * right ; }; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ Node * newNode ( int data ) { Node * node = new Node ; node -> data = data ; node -> right = node -> left = NULL ; return node ; } /* Function to print nodes of extreme corners of each level in alternate order */ void printExtremeNodes ( Node * root ) { if ( root == NULL ) return ; // Create a queue and enqueue left and right // children of root queue < Node *> q ; q . push ( root ); // flag to indicate whether leftmost node or // the rightmost node has to be printed bool flag = false ; while ( ! q . empty ()) { // nodeCount indicates number of nodes // at current level. int nodeCount = q . size (); int n = nodeCount ; // Dequeue all nodes of current level // and Enqueue all nodes of next level while ( n -- ) { Node * curr = q . front (); // Enqueue left child if ( curr -> left ) q . push ( curr -> left ); // Enqueue right child if ( curr -> right ) q . push ( curr -> right ); // Dequeue node q . pop (); // if flag is true print leftmost node if ( flag && n == nodeCount - 1 ) cout < < curr -> data < < ' ' ; // if flag is false print rightmost node if ( ! flag && n == 0 ) cout < < curr -> data < < ' ' ; } // invert flag for next level flag = ! flag ; } } /* Driver program to test above functions */ int main () { // Binary Tree of Height 4 Node * root = newNode ( 1 ); root -> left = newNode ( 2 ); root -> right = newNode ( 3 ); root -> left -> left = newNode ( 4 ); root -> left -> right = newNode ( 5 ); root -> right -> right = newNode ( 7 ); root -> left -> left -> left = newNode ( 8 ); root -> left -> left -> right = newNode ( 9 ); root -> left -> right -> left = newNode ( 10 ); root -> left -> right -> right = newNode ( 11 ); root -> right -> right -> left = newNode ( 14 ); root -> right -> right -> right = newNode ( 15 ); root -> left -> left -> left -> left = newNode ( 16 ); root -> left -> left -> left -> right = newNode ( 17 ); root -> right -> right -> right -> right = newNode ( 31 ); printExtremeNodes ( root ); return 0 ; }
Java // Java program to print nodes of extreme corners //of each level in alternate order import java.util.* ; class GFG { // A binary tree node has data pointer to left child //and a pointer to right child / static class Node { int data ; Node left right ; }; // Helper function that allocates a new node with the //given data and null left and right pointers. / static Node newNode ( int data ) { Node node = new Node (); node . data = data ; node . right = node . left = null ; return node ; } // Function to print nodes of extreme corners //of each level in alternate order static void printExtremeNodes ( Node root ) { if ( root == null ) return ; // Create a queue and enqueue left and right // children of root Queue < Node > q = new LinkedList < Node > (); q . add ( root ); // flag to indicate whether leftmost node or // the rightmost node has to be printed boolean flag = false ; while ( q . size () > 0 ) { // nodeCount indicates number of nodes // at current level. int nodeCount = q . size (); int n = nodeCount ; // Dequeue all nodes of current level // and Enqueue all nodes of next level while ( n --> 0 ) { Node curr = q . peek (); // Enqueue left child if ( curr . left != null ) q . add ( curr . left ); // Enqueue right child if ( curr . right != null ) q . add ( curr . right ); // Dequeue node q . remove (); // if flag is true print leftmost node if ( flag && n == nodeCount - 1 ) System . out . print ( curr . data + ' ' ); // if flag is false print rightmost node if ( ! flag && n == 0 ) System . out . print ( curr . data + ' ' ); } // invert flag for next level flag = ! flag ; } } // Driver code public static void main ( String args [] ) { // Binary Tree of Height 4 Node root = newNode ( 1 ); root . left = newNode ( 2 ); root . right = newNode ( 3 ); root . left . left = newNode ( 4 ); root . left . right = newNode ( 5 ); root . right . right = newNode ( 7 ); root . left . left . left = newNode ( 8 ); root . left . left . right = newNode ( 9 ); root . left . right . left = newNode ( 10 ); root . left . right . right = newNode ( 11 ); root . right . right . left = newNode ( 14 ); root . right . right . right = newNode ( 15 ); root . left . left . left . left = newNode ( 16 ); root . left . left . left . right = newNode ( 17 ); root . right . right . right . right = newNode ( 31 ); printExtremeNodes ( root ); } } // This code is contributed by Arnab Kundu
Python # Python program to print nodes of extreme corners # of each level in alternate order # Utility class to create a node class Node : def __init__ ( self key ): self . data = key self . left = self . right = None # Utility function to create a tree node def newNode ( data ): temp = Node ( 0 ) temp . data = data temp . left = temp . right = None return temp # Function to print nodes of extreme corners # of each level in alternate order def printExtremeNodes ( root ): if ( root == None ): return # Create a queue and enqueue left and right # children of root q = [] q . append ( root ) # flag to indicate whether leftmost node or # the rightmost node has to be printed flag = False while ( len ( q ) > 0 ): # nodeCount indicates number of nodes # at current level. nodeCount = len ( q ) n = nodeCount # Dequeue all nodes of current level # and Enqueue all nodes of next level while ( n > 0 ): n = n - 1 curr = q [ 0 ] # Enqueue left child if ( curr . left != None ): q . append ( curr . left ) # Enqueue right child if ( curr . right != None ): q . append ( curr . right ) # Dequeue node q . pop ( 0 ) # if flag is true print leftmost node if ( flag and n == nodeCount - 1 ): print ( curr . data end = ' ' ) # if flag is false print rightmost node if ( not flag and n == 0 ): print ( curr . data end = ' ' ) # invert flag for next level flag = not flag # Driver program to test above functions # Binary Tree of Height 4 root = newNode ( 1 ) root . left = newNode ( 2 ) root . right = newNode ( 3 ) root . left . left = newNode ( 4 ) root . left . right = newNode ( 5 ) root . right . right = newNode ( 7 ) root . left . left . left = newNode ( 8 ) root . left . left . right = newNode ( 9 ) root . left . right . left = newNode ( 10 ) root . left . right . right = newNode ( 11 ) root . right . right . left = newNode ( 14 ) root . right . right . right = newNode ( 15 ) root . left . left . left . left = newNode ( 16 ) root . left . left . left . right = newNode ( 17 ) root . right . right . right . right = newNode ( 31 ) printExtremeNodes ( root ) # This code is contributed by Arnab Kundu
C# // C# program to print nodes of extreme corners //of each level in alternate order using System ; using System.Collections.Generic ; class GFG { // A binary tree node has data pointer to left child //and a pointer to right child / public class Node { public int data ; public Node left right ; }; // Helper function that allocates a new node with the //given data and null left and right pointers. / static Node newNode ( int data ) { Node node = new Node (); node . data = data ; node . right = node . left = null ; return node ; } // Function to print nodes of extreme corners //of each level in alternate order static void printExtremeNodes ( Node root ) { if ( root == null ) return ; // Create a queue and enqueue left and right // children of root Queue < Node > q = new Queue < Node > (); q . Enqueue ( root ); // flag to indicate whether leftmost node or // the rightmost node has to be printed Boolean flag = false ; while ( q . Count > 0 ) { // nodeCount indicates number of nodes // at current level. int nodeCount = q . Count ; int n = nodeCount ; // Dequeue all nodes of current level // and Enqueue all nodes of next level while ( n --> 0 ) { Node curr = q . Peek (); // Enqueue left child if ( curr . left != null ) q . Enqueue ( curr . left ); // Enqueue right child if ( curr . right != null ) q . Enqueue ( curr . right ); // Dequeue node q . Dequeue (); // if flag is true print leftmost node if ( flag && n == nodeCount - 1 ) Console . Write ( curr . data + ' ' ); // if flag is false print rightmost node if ( ! flag && n == 0 ) Console . Write ( curr . data + ' ' ); } // invert flag for next level flag = ! flag ; } } // Driver code public static void Main ( String [] args ) { // Binary Tree of Height 4 Node root = newNode ( 1 ); root . left = newNode ( 2 ); root . right = newNode ( 3 ); root . left . left = newNode ( 4 ); root . left . right = newNode ( 5 ); root . right . right = newNode ( 7 ); root . left . left . left = newNode ( 8 ); root . left . left . right = newNode ( 9 ); root . left . right . left = newNode ( 10 ); root . left . right . right = newNode ( 11 ); root . right . right . left = newNode ( 14 ); root . right . right . right = newNode ( 15 ); root . left . left . left . left = newNode ( 16 ); root . left . left . left . right = newNode ( 17 ); root . right . right . right . right = newNode ( 31 ); printExtremeNodes ( root ); } } // This code is contributed by Rajput-Ji
JavaScript < script > // JavaScript program to print nodes of extreme corners //of each level in alternate order // A binary tree node has data pointer to left child //and a pointer to right child / class Node { constructor () { this . data = 0 ; this . left = null ; this . right = null ; } }; // Helper function that allocates a new node with the //given data and null left and right pointers. / function newNode ( data ) { var node = new Node (); node . data = data ; node . right = node . left = null ; return node ; } // Function to print nodes of extreme corners //of each level in alternate order function printExtremeNodes ( root ) { if ( root == null ) return ; // Create a queue and enqueue left and right // children of root var q = []; q . push ( root ); // flag to indicate whether leftmost node or // the rightmost node has to be printed var flag = false ; while ( q . length > 0 ) { // nodeCount indicates number of nodes // at current level. var nodeCount = q . length ; var n = nodeCount ; // Dequeue all nodes of current level // and push all nodes of next level while ( n --> 0 ) { var curr = q [ 0 ]; // push left child if ( curr . left != null ) q . push ( curr . left ); // push right child if ( curr . right != null ) q . push ( curr . right ); // Dequeue node q . shift (); // if flag is true print leftmost node if ( flag && n == nodeCount - 1 ) document . write ( curr . data + ' ' ); // if flag is false print rightmost node if ( ! flag && n == 0 ) document . write ( curr . data + ' ' ); } // invert flag for next level flag = ! flag ; } } // Driver code // Binary Tree of Height 4 var root = newNode ( 1 ); root . left = newNode ( 2 ); root . right = newNode ( 3 ); root . left . left = newNode ( 4 ); root . left . right = newNode ( 5 ); root . right . right = newNode ( 7 ); root . left . left . left = newNode ( 8 ); root . left . left . right = newNode ( 9 ); root . left . right . left = newNode ( 10 ); root . left . right . right = newNode ( 11 ); root . right . right . left = newNode ( 14 ); root . right . right . right = newNode ( 15 ); root . left . left . left . left = newNode ( 16 ); root . left . left . left . right = newNode ( 17 ); root . right . right . right . right = newNode ( 31 ); printExtremeNodes ( root ); < /script>
산출
1 2 7 8 31
시간 복잡도: O(n) 여기서 n은 주어진 이진 트리의 총 노드 수입니다.
보조 공간: O(n) 여기서 n은 대기열로 인해 주어진 이진 트리의 총 노드 수입니다.
운동 - 각 레벨의 맨 끝 모서리에 있는 노드를 아래에서 위로 교대로 인쇄합니다.