대괄호 형식으로 문자열을 나누는 모든 방법을 인쇄합니다.
문자열이 주어지면 주어진 문자열을 대괄호 형식으로 나누는 모든 방법을 찾으십시오. 각 하위 문자열을 괄호로 묶습니다.
예:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
브라우저를 최소화하고 먼저 직접 시도해 보시기 바랍니다.
아이디어는 재귀를 사용하는 것입니다. 처리할 다음 문자의 인덱스와 지금까지의 출력 문자열이라는 두 개의 매개변수를 유지합니다. 처리할 다음 문자의 인덱스부터 시작하여 처리되지 않은 문자열로 구성된 하위 문자열을 출력 문자열에 추가하고 전체 문자열을 처리할 때까지 나머지 문자열을 반복합니다. std::substr을 사용하여 출력 문자열을 구성합니다. substr(pos n)은 현재 문자열의 위치 pos에서 시작하는 길이 n의 하위 문자열을 반환합니다.
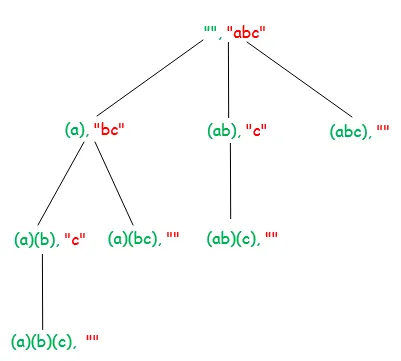
아래 다이어그램은 입력 문자열 'abc'에 대한 재귀 트리를 보여줍니다. 다이어그램의 각 노드에는 처리된 문자열(녹색으로 표시)과 처리되지 않은 문자열(빨간색으로 표시)이 표시됩니다.

아래는 위의 아이디어를 구현한 것입니다.
C++ // C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include using namespace std ; // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far void findCombinations ( string str int index string out ) { if ( index == str . length ()) cout < < out < < endl ; for ( int i = index ; i < str . length (); i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substr ( index i + 1 - index ) + ')' ); } } // Driver Code int main () { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); return 0 ; }
Java // Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations ( String str int index String out ) { if ( index == str . length ()) System . out . println ( out ); for ( int i = index ; i < str . length (); i ++ ) // append substring formed by str[index // i] to output string findCombinations ( str i + 1 out + '(' + str . substring ( index i + 1 ) + ')' ); } // Driver Code public static void main ( String [] args ) { // input string String str = 'abcd' ; findCombinations ( str 0 '' ); } } // Contributed by Pramod Kumar
Python3 # Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations ( string index out ): if index == len ( string ): print ( out ) for i in range ( index len ( string ) 1 ): # append substring formed by str[index # i] to output string findCombinations ( string i + 1 out + '(' + string [ index : i + 1 ] + ')' ) # Driver Code if __name__ == '__main__' : # input string string = 'abcd' findCombinations ( string 0 '' ) # This code is contributed by # sanjeev2552
C# // C# program to find all combinations // of Non-overlapping substrings formed // from given string using System ; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations ( string str int index string @out ) { if ( index == str . Length ) { Console . WriteLine ( @out ); } for ( int i = index ; i < str . Length ; i ++ ) { // append substring formed by // str[index i] to output string findCombinations ( str i + 1 @out + '(' + str . Substring ( index ( i + 1 ) - index ) + ')' ); } } // Driver Code public static void Main ( string [] args ) { // input string string str = 'abcd' ; findCombinations ( str 0 '' ); } } // This code is contributed by Shrikant13
JavaScript // Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations ( string index out ) { if ( index == string . length ) { console . log ( out ); } for ( let i = index ; i < string . length ; i ++ ) { // append substring formed by str[index // i] to output string findCombinations ( string i + 1 out + '(' + string . substring ( index i + 1 ) + ')' ); } } // Driver Code const string = 'abcd' ; findCombinations ( string 0 '' ); // contributed by adityasharmadev01
산출
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
시간 복잡도: O(N 2 )
보조 공간: O(N 2 )