총 거리를 최소화하는 최적의 지점 위치

GfG Practice에서 사용해 보세요.  #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; }
산출
 #practiceLinkDiv { 표시: 없음 !중요; }
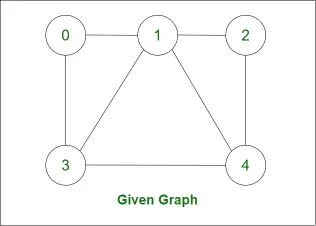
#practiceLinkDiv { 표시: 없음 !중요; } 점 집합과 ax+by+c = 0인 선이 주어지면 주어진 점 집합으로부터의 거리 합이 최소가 되는 주어진 선에서 점을 찾아야 합니다.
예:

In above figure optimum location of point of x - y - 3 = 0 line is (2 -1) whose total distance with other points is 20.77 which is minimum obtainable total distance.Recommended Practice 총 거리를 최소화하는 최적의 지점 위치 시도해 보세요!
무한 거리에서 주어진 선의 한 점을 취하면 이제 이 점을 주어진 점 쪽으로 이동하면 총 거리 비용은 무한해집니다. 총 거리 비용은 감소하기 시작하고 얼마 후 다시 증가하기 시작하여 선의 다른 무한 끝에서 무한에 도달하므로 거리 비용 곡선은 U-곡선처럼 보이고 이 U-곡선의 최저 값을 찾아야 합니다.
U-곡선은 단조롭게 증가하거나 감소하지 않으므로 여기서는 최하위 지점을 찾기 위해 이진 검색을 사용할 수 없습니다. 삼항 검색은 각 반복에서 검색 공간의 1/3을 건너뜁니다. 삼항 검색에 대해 자세히 읽을 수 있습니다. 여기 .
따라서 솔루션은 다음과 같이 진행됩니다. 각각 가장 작은 값과 가장 큰 값으로 초기화된 low 및 high로 시작한 다음 각 반복에서 반복을 시작합니다. 검색 공간에서 1/3 및 2/3 위치를 나타내는 두 개의 mid mid1 및 mid2를 계산합니다. mid1 및 mid2가 있는 모든 점의 총 거리를 계산하고 이러한 거리 비용을 비교하여 low 또는 high를 업데이트합니다. 이 반복은 low와 high가 대략 같아질 때까지 계속됩니다.
C++ // C/C++ program to find optimum location and total cost #include using namespace std ; #define sq(x) ((x) * (x)) #define EPS 1e-6 #define N 5 // structure defining a point struct point { int x y ; point () {} point ( int x int y ) : x ( x ) y ( y ) { } }; // structure defining a line of ax + by + c = 0 form struct line { int a b c ; line ( int a int b int c ) : a ( a ) b ( b ) c ( c ) { } }; // method to get distance of point (x y) from point p double dist ( double x double y point p ) { return sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = -1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance double findOptimumCostUtil ( point p [] int n line l ) { double low = -1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x co-ordiantes // of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; // double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost double findOptimumCost ( int points [ N ][ 2 ] line l ) { point p [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver code to test above method int main () { line l ( 1 -1 -3 ); int points [ N ][ 2 ] = { { -3 -2 } { -1 0 } { -1 2 } { 1 2 } { 3 4 } }; cout < < findOptimumCost ( points l ) < < endl ; return 0 ; }
Java // A Java program to find optimum location // and total cost class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point static class point { int x y ; point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line of ax + by + c = 0 form static class line { int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of point (x y) from point p static double dist ( double x double y point p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ static double compute ( point p [] int n line l double X ) { double res = 0 ; // calculating Y of chosen point by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ] ); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point p [] int n line l ) { double low = - 1e6 ; double high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int points [][] line l ) { point [] p = new point [ N ] ; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ] ); return findOptimumCostUtil ( p N l ); } // Driver Code public static void main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int points [][] = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; System . out . println ( findOptimumCost ( points l )); } } // This code is contributed by Rajput-Ji
Python3 # A Python3 program to find optimum location # and total cost import math class Optimum_distance : # Class defining a point class Point : def __init__ ( self x y ): self . x = x self . y = y # Class defining a line of ax + by + c = 0 form class Line : def __init__ ( self a b c ): self . a = a self . b = b self . c = c # Method to get distance of point # (x y) from point p def dist ( self x y p ): return math . sqrt (( x - p . x ) ** 2 + ( y - p . y ) ** 2 ) # Utility method to compute total distance # all points when choose point on given # line has x-coordinate value as X def compute ( self p n l x ): res = 0 y = - 1 * ( l . a * x + l . c ) / l . b # Calculating Y of chosen point # by line equation for i in range ( n ): res += self . dist ( x y p [ i ]) return res # Utility method to find minimum total distance def find_Optimum_cost_untill ( self p n l ): low = - 1e6 high = 1e6 eps = 1e-6 + 1 # Loop until difference between low # and high become less than EPS while (( high - low ) > eps ): # mid1 and mid2 are representative x # co-ordiantes of search space mid1 = low + ( high - low ) / 3 mid2 = high - ( high - low ) / 3 dist1 = self . compute ( p n l mid1 ) dist2 = self . compute ( p n l mid2 ) # If mid2 point gives more total # distance skip third part if ( dist1 < dist2 ): high = mid2 # If mid1 point gives more total # distance skip first part else : low = mid1 # Compute optimum distance cost by # sending average of low and high as X return self . compute ( p n l ( low + high ) / 2 ) # Method to find optimum cost def find_Optimum_cost ( self p l ): n = len ( p ) p_arr = [ None ] * n # Converting 2D array input to point array for i in range ( n ): p_obj = self . Point ( p [ i ][ 0 ] p [ i ][ 1 ]) p_arr [ i ] = p_obj return self . find_Optimum_cost_untill ( p_arr n l ) # Driver Code if __name__ == '__main__' : obj = Optimum_distance () l = obj . Line ( 1 - 1 - 3 ) p = [ [ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ] ] print ( obj . find_Optimum_cost ( p l )) # This code is contributed by Sulu_mufi
C# // C# program to find optimum location // and total cost using System ; class GFG { static double sq ( double x ) { return (( x ) * ( x )); } static int EPS = ( int )( 1e-6 ) + 1 ; static int N = 5 ; // structure defining a point public class point { public int x y ; public point () {} public point ( int x int y ) { this . x = x ; this . y = y ; } }; // structure defining a line // of ax + by + c = 0 form public class line { public int a b c ; public line ( int a int b int c ) { this . a = a ; this . b = b ; this . c = c ; } }; // method to get distance of // point (x y) from point p static double dist ( double x double y point p ) { return Math . Sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance of all points when choose point on given line has x-coordinate value as X */ static double compute ( point [] p int n line l double X ) { double res = 0 ; // calculating Y of chosen point // by line equation double Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( int i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance static double findOptimumCostUtil ( point [] p int n line l ) { double low = - 1 e6 ; double high = 1 e6 ; // loop until difference between // low and high become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative // x co-ordiantes of search space double mid1 = low + ( high - low ) / 3 ; double mid2 = high - ( high - low ) / 3 ; double dist1 = compute ( p n l mid1 ); double dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by // sending average of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost static double findOptimumCost ( int [ ] points line l ) { point [] p = new point [ N ]; // converting 2D array input to point array for ( int i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i 0 ] points [ i 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code public static void Main ( String [] args ) { line l = new line ( 1 - 1 - 3 ); int [ ] points = { { - 3 - 2 } { - 1 0 } { - 1 2 } { 1 2 } { 3 4 } }; Console . WriteLine ( findOptimumCost ( points l )); } } // This code is contributed by 29AjayKumar
JavaScript < script > // A JavaScript program to find optimum location // and total cost function sq ( x ) { return x * x ; } let EPS = ( 1e-6 ) + 1 ; let N = 5 ; // structure defining a point class point { constructor ( x y ) { this . x = x ; this . y = y ; } } // structure defining a line of ax + by + c = 0 form class line { constructor ( a b c ) { this . a = a ; this . b = b ; this . c = c ; } } // method to get distance of point (x y) from point p function dist ( x y p ) { return Math . sqrt ( sq ( x - p . x ) + sq ( y - p . y )); } /* Utility method to compute total distance all points when choose point on given line has x-coordinate value as X */ function compute ( p n l X ) { let res = 0 ; // calculating Y of chosen point by line equation let Y = - 1 * ( l . c + l . a * X ) / l . b ; for ( let i = 0 ; i < n ; i ++ ) res += dist ( X Y p [ i ]); return res ; } // Utility method to find minimum total distance function findOptimumCostUtil ( p n l ) { let low = - 1e6 ; let high = 1e6 ; // loop until difference between low and high // become less than EPS while (( high - low ) > EPS ) { // mid1 and mid2 are representative x // co-ordiantes of search space let mid1 = low + ( high - low ) / 3 ; let mid2 = high - ( high - low ) / 3 ; let dist1 = compute ( p n l mid1 ); let dist2 = compute ( p n l mid2 ); // if mid2 point gives more total distance // skip third part if ( dist1 < dist2 ) high = mid2 ; // if mid1 point gives more total distance // skip first part else low = mid1 ; } // compute optimum distance cost by sending average // of low and high as X return compute ( p n l ( low + high ) / 2 ); } // method to find optimum cost function findOptimumCost ( points l ) { let p = new Array ( N ); // converting 2D array input to point array for ( let i = 0 ; i < N ; i ++ ) p [ i ] = new point ( points [ i ][ 0 ] points [ i ][ 1 ]); return findOptimumCostUtil ( p N l ); } // Driver Code let l = new line ( 1 - 1 - 3 ); let points = [[ - 3 - 2 ] [ - 1 0 ] [ - 1 2 ] [ 1 2 ] [ 3 4 ]]; document . write ( findOptimumCost ( points l )); // This code is contributed by rag2127 < /script>
산출
20.7652
시간 복잡도: 에 2 )
보조 공간: 에)