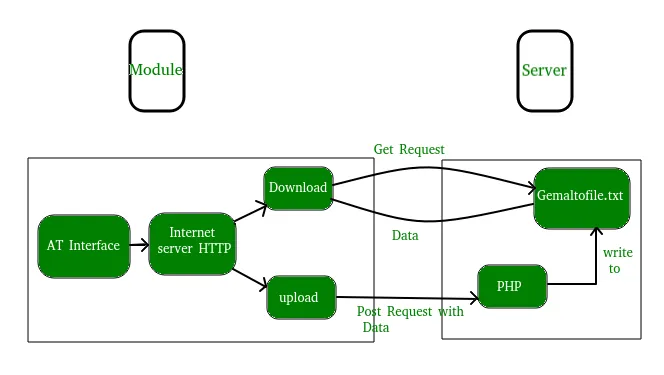
선형 회귀(Python 구현)
이 기사에서는 선형 회귀의 기본 사항과 Python 프로그래밍 언어로 구현하는 방법에 대해 설명합니다. 선형 회귀는 종속 변수와 주어진 독립 변수 세트 간의 관계를 모델링하기 위한 통계 방법입니다.
메모: 이 글에서는 종속변수를 다음과 같이 지칭합니다. 응답 독립 변수는 다음과 같습니다. 특징 단순성을 위해. 선형 회귀에 대한 기본적인 이해를 제공하기 위해 가장 기본적인 선형 회귀 버전부터 시작합니다. 단순 선형 회귀 .
선형 회귀란 무엇입니까?
선형 회귀 하나 이상의 독립변수(예측변수)를 기반으로 연속형 종속변수(목표변수)를 예측하는데 사용되는 통계적 방법이다. 이 기법은 종속변수와 독립변수 사이의 선형 관계를 가정합니다. 이는 종속변수가 독립변수의 변화에 비례하여 변화한다는 것을 의미합니다. 즉, 선형 회귀는 하나 이상의 변수가 종속 변수의 값을 예측할 수 있는 정도를 결정하는 데 사용됩니다.
선형 회귀 모델에서 가정하는 사항:
선형 회귀 모델이 적용되는 데이터 세트와 관련하여 만드는 기본 가정은 다음과 같습니다.
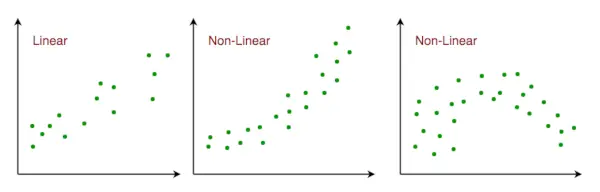
- 선형 관계 : 응답변수와 특성변수의 관계는 선형이어야 합니다. 선형성 가정은 산점도를 사용하여 테스트할 수 있습니다. 아래에 표시된 것처럼 첫 번째 그림은 선형적으로 관련된 변수를 나타내는 반면, 두 번째 및 세 번째 그림의 변수는 비선형일 가능성이 높습니다. 따라서 첫 번째 그림은 선형 회귀를 사용하여 더 나은 예측을 제공합니다.

특징 공간과 선형 관계
- 다중 공선성이 거의 또는 전혀 없음 : 데이터에 다중공선성이 거의 없거나 전혀 없다고 가정합니다. 다중 공선성은 특성(또는 독립 변수)이 서로 독립적이지 않을 때 발생합니다.
- 자기 상관이 거의 또는 전혀 없음 : 또 다른 가정은 데이터에 자기상관이 거의 없거나 전혀 없다는 것입니다. 자기상관은 잔차 오차가 서로 독립적이지 않을 때 발생합니다. 이 주제에 대한 자세한 내용은 여기를 참조하세요.
- 이상치 없음: 데이터에 이상값이 없다고 가정합니다. 이상값은 나머지 데이터와 멀리 떨어져 있는 데이터 포인트입니다. 이상치는 분석 결과에 영향을 미칠 수 있습니다.
- 동질성 : 동분산성(homoscedasticity)은 오차항(즉, 독립변수와 종속변수 사이의 관계에 있는 잡음이나 무작위적 교란)이 모든 독립변수 값에서 동일한 상황을 말합니다. 아래 그림과 같이 그림 1에는 등분산성이 있고 그림 2에는 이분산성이 있습니다.

선형 회귀 분석의 동질성
이 기사가 끝나면 아래에서 선형 회귀의 몇 가지 응용 프로그램에 대해 논의합니다.
선형 회귀 유형
선형 회귀에는 두 가지 주요 유형이 있습니다.
- 단순 선형 회귀: 여기에는 단일 독립 변수를 기반으로 종속 변수를 예측하는 작업이 포함됩니다.
- 다중 선형 회귀: 여기에는 여러 독립 변수를 기반으로 종속 변수를 예측하는 작업이 포함됩니다.
단순 선형 회귀
단순한 선형 회귀 예측하는 접근 방식이다. 응답 사용하여 단일 기능 . 가장 기본적인 것 중 하나죠 기계 학습 기계 학습 애호가가 알게 되는 모델입니다. 선형 회귀 분석에서는 두 변수, 즉 종속 변수와 독립 변수가 선형 관계에 있다고 가정합니다. 따라서 우리는 특성이나 독립변수(x)의 함수로서 응답값(y)을 최대한 정확하게 예측하는 선형함수를 찾으려고 노력합니다. 모든 특성 x에 대해 응답 y 값이 있는 데이터 세트를 고려해 보겠습니다.

일반적으로 다음과 같이 정의합니다.
x로 특징 벡터 , 즉 x = [x_1, x_2, …., x_n],
그래서 응답 벡터 , 즉 y = [y_1, y_2, …., y_n]
~을 위한 N 관찰(위 예에서는 n=10). 위 데이터 세트의 산점도는 다음과 같습니다.

무작위로 생성된 데이터에 대한 산점도
이제 과제는 찾는 일이다. 가장 잘 어울리는 라인 위의 산점도에서 새로운 특성 값에 대한 반응을 예측할 수 있습니다. (즉, 데이터세트에 x 값이 존재하지 않음) 이 라인을 회귀선 . 회귀선의 방정식은 다음과 같이 표현됩니다.
여기,
- h(x_i)는 예측된 반응 값 나를 위해 일 관찰.
- b_0과 b_1은 회귀계수이며 y절편 그리고 경사 회귀선의 각각.
모델을 만들려면 회귀 계수 b_0 및 b_1의 값을 학습하거나 추정해야 합니다. 그리고 이러한 계수를 추정한 후에는 모델을 사용하여 응답을 예측할 수 있습니다!
이번 글에서는 원리를 활용해 보겠습니다. 최소제곱 .
이제 다음을 고려하십시오.
여기서 e_i는 잔여 오류 i 번째 관찰에서. 따라서 우리의 목표는 전체 잔여 오류를 최소화하는 것입니다. 제곱 오차 또는 비용 함수 J를 다음과 같이 정의합니다.
그리고 우리의 임무는 b의 값을 찾는 것입니다. 0 그리고 b 1 J(b 0 , 비 1 )은 최소입니다! 수학적 세부 사항을 다루지 않고 여기에 결과를 제시합니다.
SS는 어디에 xy 는 y와 x의 교차편차의 합입니다.
그리고 SS 더블 엑스 x의 편차 제곱의 합입니다.
단순 선형 회귀의 Python 구현
우리는 파이썬 선형 회귀 모델의 계수를 학습하는 언어입니다. 입력 데이터와 가장 적합한 선을 그리기 위해 다음을 사용합니다. matplotlib 도서관. 그래프를 그리는 데 가장 많이 사용되는 Python 라이브러리 중 하나입니다. 다음은 Python을 사용한 간단한 선형 회귀의 예입니다.
라이브러리 가져오기
파이썬3
import> numpy as np> import> matplotlib.pyplot as plt> |
Estimating Coefficients Function This function, estimate_coef(), takes the input data x (independent variable) and y (dependent variable) and estimates the coefficients of the linear regression line using the least squares method. Calculating Number of Observations: n = np.size(x) determines the number of data points. Calculating Means: m_x = np.mean(x) and m_y = np.mean(y) compute the mean values of x and y, respectively. Calculating Cross-Deviation and Deviation about x: SS_xy = np.sum(y*x) - n*m_y*m_x and SS_xx = np.sum(x*x) - n*m_x*m_x calculate the sum of squared deviations between x and y and the sum of squared deviations of x about its mean, respectively. Calculating Regression Coefficients: b_1 = SS_xy / SS_xx and b_0 = m_y - b_1*m_x determine the slope (b_1) and intercept (b_0) of the regression line using the least squares method. Returning Coefficients: The function returns the estimated coefficients as a tuple (b_0, b_1). Python3 def estimate_coef(x, y): # number of observations/points n = np.size(x) # mean of x and y vector m_x = np.mean(x) m_y = np.mean(y) # calculating cross-deviation and deviation about x SS_xy = np.sum(y*x) - n*m_y*m_x SS_xx = np.sum(x*x) - n*m_x*m_x # calculating regression coefficients b_1 = SS_xy / SS_xx b_0 = m_y - b_1*m_x return (b_0, b_1) Plotting Regression Line Function This function, plot_regression_line(), takes the input data x (independent variable), y (dependent variable), and the estimated coefficients b to plot the regression line and the data points. Plotting Scatter Plot: plt.scatter(x, y, color = 'm', marker = 'o', s = 30) plots the original data points as a scatter plot with red markers. Calculating Predicted Response Vector: y_pred = b[0] + b[1]*x calculates the predicted values for y based on the estimated coefficients b. Plotting Regression Line: plt.plot(x, y_pred, color = 'g') plots the regression line using the predicted values and the independent variable x. Adding Labels: plt.xlabel('x') and plt.ylabel('y') label the x-axis as 'x' and the y-axis as 'y', respectively. Python3 def plot_regression_line(x, y, b): # plotting the actual points as scatter plot plt.scatter(x, y, color = 'm', marker = 'o', s = 30) # predicted response vector y_pred = b[0] + b[1]*x # plotting the regression line plt.plot(x, y_pred, color = 'g') # putting labels plt.xlabel('x') plt.ylabel('y') Output: Scatterplot of the points along with the regression line Main Function The provided code implements simple linear regression analysis by defining a function main() that performs the following steps: Data Definition: Defines the independent variable (x) and dependent variable (y) as NumPy arrays. Coefficient Estimation: Calls the estimate_coef() function to determine the coefficients of the linear regression line using the provided data. Printing Coefficients: Prints the estimated intercept (b_0) and slope (b_1) of the regression line. Python3 def main(): # observations / data x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12]) # estimating coefficients b = estimate_coef(x, y) print('Estimated coefficients:
b_0 = {}
b_1 = {}'.format(b Output: Estimated coefficients: b_0 = -0.0586206896552 b_1 = 1.45747126437Multiple Linear RegressionMultiple linear regression attempts to model the relationship between two or more features and a response by fitting a linear equation to the observed data. Clearly, it is nothing but an extension of simple linear regression. Consider a dataset with p features(or independent variables) and one response(or dependent variable). Also, the dataset contains n rows/observations. We define: X ( feature matrix ) = a matrix of size n X p where xij denotes the values of the jth feature for ith observation. So, and y ( response vector ) = a vector of size n where y_{i} denotes the value of response for ith observation. The regression line for p features is represented as: where h(x_i) is predicted response value for ith observation and b_0, b_1, …, b_p are the regression coefficients . Also, we can write: where e_i represents a residual error in ith observation. We can generalize our linear model a little bit more by representing feature matrix X as: So now, the linear model can be expressed in terms of matrices as: where, and Now, we determine an estimate of b , i.e. b’ using the Least Squares method . As already explained, the Least Squares method tends to determine b’ for which total residual error is minimized. We present the result directly here: where ‘ represents the transpose of the matrix while -1 represents the matrix inverse . Knowing the least square estimates, b’, the multiple linear regression model can now be estimated as: where y’ is the estimated response vector . Python Implementation of Multiple Linear Regression For multiple linear regression using Python, we will use the Boston house pricing dataset. Importing Libraries Python3 from sklearn.model_selection import train_test_split import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model, metrics import pandas as pd Loading the Boston Housing Dataset The code downloads the Boston Housing dataset from the provided URL and reads it into a Pandas DataFrame (raw_df) Python3 data_url = ' http://lib.stat.cmu.edu/datasets/boston ' raw_df = pd.read_csv(data_url, sep='s+', skiprows=22, header=None) Preprocessing Data This extracts the input variables (X) and target variable (y) from the DataFrame. The input variables are selected from every other row to match the target variable, which is available every other row. Python3 X = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]]) y = raw_df.values[1::2, 2] Splitting Data into Training and Testing Sets Here it divides the data into training and testing sets using the train_test_split() function from scikit-learn. The test_size parameter specifies that 40% of the data should be used for testing. Python3 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) Creating and Training the Linear Regression Model This initializes a LinearRegression object (reg) and trains the model using the training data (X_train, y_train) Python3 reg = linear_model.LinearRegression() reg.fit(X_train, y_train) Evaluating Model Performance Evaluates the model’s performance by printing the regression coefficients and calculating the variance score, which measures the proportion of explained variance. A score of 1 indicates perfect prediction. Python3 # regression coefficients print('Coefficients: ', reg.coef_) # variance score: 1 means perfect prediction print('Variance score: {}'.format(reg.score(X_test, y_test))) Output: Coefficients: [ -8.80740828e-02 6.72507352e-02 5.10280463e-02 2.18879172e+00 -1.72283734e+01 3.62985243e+00 2.13933641e-03 -1.36531300e+00 2.88788067e-01 -1.22618657e-02 -8.36014969e-01 9.53058061e-03 -5.05036163e-01] Variance score: 0.720898784611 Plotting Residual Errors Plotting and analyzing the residual errors, which represent the difference between the predicted values and the actual values. Python3 # plot for residual error # setting plot style plt.style.use('fivethirtyeight') # plotting residual errors in training data plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train, color='green', s=10, label='Train data') # plotting residual errors in test data plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test, color='blue', s=10, label='Test data') # plotting line for zero residual error plt.hlines(y=0, xmin=0, xmax=50, linewidth=2) # plotting legend plt.legend(loc='upper right') # plot title plt.title('Residual errors') # method call for showing the plot plt.show() Output: Residual Error Plot for the Multiple Linear Regression In the above example, we determine the accuracy score using Explained Variance Score . We define: explained_variance_score = 1 – Var{y – y’}/Var{y} where y’ is the estimated target output, y is the corresponding (correct) target output, and Var is Variance, the square of the standard deviation. The best possible score is 1.0, lower values are worse. Polynomial Linear Regression Polynomial Regression is a form of linear regression in which the relationship between the independent variable x and dependent variable y is modeled as an nth-degree polynomial. Polynomial regression fits a nonlinear relationship between the value of x and the corresponding conditional mean of y, denoted E(y | x). Choosing a Degree for Polynomial Regression The choice of degree for polynomial regression is a trade-off between bias and variance. Bias is the tendency of a model to consistently predict the same value, regardless of the true value of the dependent variable. Variance is the tendency of a model to make different predictions for the same data point, depending on the specific training data used. A higher-degree polynomial can reduce bias but can also increase variance, leading to overfitting. Conversely, a lower-degree polynomial can reduce variance but can also increase bias. There are a number of methods for choosing a degree for polynomial regression, such as cross-validation and using information criteria such as Akaike information criterion (AIC) or Bayesian information criterion (BIC). Implementation of Polynomial Regression using Python Implementing the Polynomial regression using Python: Here we will import all the necessary libraries for data analysis and machine learning tasks and then loads the ‘Position_Salaries.csv’ dataset using Pandas. It then prepares the data for modeling by handling missing values and encoding categorical data. Finally, it splits the data into training and testing sets and standardizes the numerical features using StandardScaler. Python3 import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import sklearn import warnings from sklearn.preprocessing import LabelEncoder from sklearn.impute import KNNImputer from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.metrics import f1_score from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import cross_val_score warnings.filterwarnings('ignore') df = pd.read_csv('Position_Salaries.csv') X = df.iloc[:,1:2].values y = df.iloc[:,2].values x Output: array([[ 1, 45000, 0], [ 2, 50000, 4], [ 3, 60000, 8], [ 4, 80000, 5], [ 5, 110000, 3], [ 6, 150000, 7], [ 7, 200000, 6], [ 8, 300000, 9], [ 9, 500000, 1], [ 10, 1000000, 2]], dtype=int64) The code creates a linear regression model and fits it to the provided data, establishing a linear relationship between the independent and dependent variables. Python3 from sklearn.linear_model import LinearRegression lin_reg=LinearRegression() lin_reg.fit(X,y) The code performs quadratic and cubic regression by generating polynomial features from the original data and fitting linear regression models to these features. This enables modeling nonlinear relationships between the independent and dependent variables. Python3 from sklearn.preprocessing import PolynomialFeatures poly_reg2=PolynomialFeatures(degree=2) X_poly=poly_reg2.fit_transform(X) lin_reg_2=LinearRegression() lin_reg_2.fit(X_poly,y) poly_reg3=PolynomialFeatures(degree=3) X_poly3=poly_reg3.fit_transform(X) lin_reg_3=LinearRegression() lin_reg_3.fit(X_poly3,y) The code creates a scatter plot of the data point, It effectively visualizes the linear relationship between position level and salary. Python3 plt.scatter(X,y,color='red') plt.plot(X,lin_reg.predict(X),color='green') plt.title('Simple Linear Regression') plt.xlabel('Position Level') plt.ylabel('Salary') plt.show() Output: The code creates a scatter plot of the data points, overlays the predicted quadratic and cubic regression lines. It effectively visualizes the nonlinear relationship between position level and salary and compares the fits of quadratic and cubic regression models. Python3 plt.style.use('fivethirtyeight') plt.scatter(X,y,color='red') plt.plot(X,lin_reg_2.predict(poly_reg2.fit_transform(X)),color='green') plt.plot(X,lin_reg_3.predict(poly_reg3.fit_transform(X)),color='yellow') plt.title('Polynomial Linear Regression Degree 2') plt.xlabel('Position Level') plt.ylabel('Salary') plt.show() Output: The code effectively visualizes the relationship between position level and salary using cubic regression and generates a continuous prediction line for a broader range of position levels. Python3 plt.style.use('fivethirtyeight') X_grid=np.arange(min(X),max(X),0.1) # This will give us a vector.We will have to convert this into a matrix X_grid=X_grid.reshape((len(X_grid),1)) plt.scatter(X,y,color='red') plt.plot(X_grid,lin_reg_3.predict(poly_reg3.fit_transform(X_grid)),color='lightgreen') #plt.plot(X,lin_reg_3.predict(poly_reg3.fit_transform(X)),color='green') plt.title('Polynomial Linear Regression Degree 3') plt.xlabel('Position Level') plt.ylabel('Salary') plt.show() Output: Applications of Linear Regression Trend lines: A trend line represents the variation in quantitative data with the passage of time (like GDP, oil prices, etc.). These trends usually follow a linear relationship. Hence, linear regression can be applied to predict future values. However, this method suffers from a lack of scientific validity in cases where other potential changes can affect the data. Economics: Linear regression is the predominant empirical tool in economics. For example, it is used to predict consumer spending, fixed investment spending, inventory investment, purchases of a country’s exports, spending on imports, the demand to hold liquid assets, labor demand, and labor supply. Finance: The capital price asset model uses linear regression to analyze and quantify the systematic risks of an investment. Biology: Linear regression is used to model causal relationships between parameters in biological systems. Advantages of Linear Regression Easy to interpret: The coefficients of a linear regression model represent the change in the dependent variable for a one-unit change in the independent variable, making it simple to comprehend the relationship between the variables. Robust to outliers: Linear regression is relatively robust to outliers meaning it is less affected by extreme values of the independent variable compared to other statistical methods. Can handle both linear and nonlinear relationships: Linear regression can be used to model both linear and nonlinear relationships between variables. This is because the independent variable can be transformed before it is used in the model. No need for feature scaling or transformation: Unlike some machine learning algorithms, linear regression does not require feature scaling or transformation. This can be a significant advantage, especially when dealing with large datasets. Disadvantages of Linear Regression Assumes linearity: Linear regression assumes that the relationship between the independent variable and the dependent variable is linear. This assumption may not be valid for all data sets. In cases where the relationship is nonlinear, linear regression may not be a good choice. Sensitive to multicollinearity: Linear regression is sensitive to multicollinearity. This occurs when there is a high correlation between the independent variables. Multicollinearity can make it difficult to interpret the coefficients of the model and can lead to overfitting. May not be suitable for highly complex relationships: Linear regression may not be suitable for modeling highly complex relationships between variables. For example, it may not be able to model relationships that include interactions between the independent variables. Not suitable for classification tasks: Linear regression is a regression algorithm and is not suitable for classification tasks, which involve predicting a categorical variable rather than a continuous variable.Frequently Asked Question(FAQs)1. How to use linear regression to make predictions? Once a linear regression model has been trained, it can be used to make predictions for new data points. The scikit-learn LinearRegression class provides a method called predict() that can be used to make predictions. 2. What is linear regression? Linear regression is a supervised machine learning algorithm used to predict a continuous numerical output. It assumes that the relationship between the independent variables (features) and the dependent variable (target) is linear, meaning that the predicted value of the target can be calculated as a linear combination of the features. 3. How to perform linear regression in Python? There are several libraries in Python that can be used to perform linear regression, including scikit-learn, statsmodels, and NumPy. The scikit-learn library is the most popular choice for machine learning tasks, and it provides a simple and efficient implementation of linear regression. 4. What are some applications of linear regression? Linear regression is a versatile algorithm that can be used for a wide variety of applications, including finance, healthcare, and marketing. Some specific examples include: Predicting house pricesPredicting stock pricesDiagnosing medical conditionsPredicting customer churn5. How linear regression is implemented in sklearn?Linear regression is implemented in scikit-learn using the LinearRegression class. This class provides methods to fit a linear regression model to a training dataset and predict the target value for new data points.