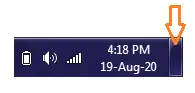
지수의 법칙

지수의 법칙: 지수는 매우 크거나 작은 숫자를 나타내는 방법입니다. 지수 규칙은 다양한 지수 문제를 해결하는 데 사용되는 지수의 법칙입니다. 이러한 지수 법칙을 사용하여 지수에 대한 곱셈, 나눗셈 및 기타 연산을 수행할 수 있습니다. 수학에는 지수 법칙이라고도 불리는 다양한 지수 규칙이 있으며 이러한 모든 법칙은 아래 기사에 추가됩니다.
이 기사에서는 다음에 대해 알아볼 것입니다. 지수 정의, 지수 법칙, 지수 법칙 예 및 기타 세부 사항.
내용의 테이블
- 지수 정의
- 지수 규칙이란 무엇입니까?
- 지수의 법칙이란 무엇입니까?
- 거듭제곱 법칙의 산물
- 거듭제곱의 법칙
- 거듭제곱 법칙의 힘
- 제품 규칙의 힘
- 몫의 법칙의 거듭제곱
- 제로 전력 규칙
- 음수 지수 규칙
- 분수 지수 규칙(분수를 포함한 지수의 법칙)
- 기타 지수 규칙
- 지수와 로그의 법칙
- 표: 지수의 법칙
- 지수 규칙 예
지수 정의
숫자가 어느 정도 거듭제곱되면 기본 숫자의 거듭제곱을 지수라고 합니다. 지수는 단순히 기본 숫자에 언급된 거듭제곱만큼 자체적으로 곱해지는 것을 의미합니다.
예를 들어 P라고 하면 N 이는 P에 'n'을 여러 번 곱한다는 의미입니다. P×P×P×P×P×P 로 확장할 수 있습니다. . . n 번.
5라고 해보자 삼 = 5 × 5 × 5 = 125; 방정식은 5의 3제곱으로 읽혀집니다.
지수가 2이면 제곱이라고도 하고, 지수가 3이면 세제곱이라고도 합니다. 면적을 계산할 때는 길이(m/cm)를 2번 곱하기 때문에 '제곱'이라는 용어를 사용하고, 부피의 경우 길이(단위 = m/cm)를 3번 곱하여 '큐브'라는 용어를 사용합니다. 타임스.
Expont는 아주 작은 양뿐만 아니라 아주 큰 양을 쓰는 데 도움이 됩니다. 예를 들어, 5.97219×10인 지구의 질량과 같은 큰 양을 쓸 수 있습니다. 24 kg 뿐만 아니라 전자의 질량이 9.1×10 -31 킬로그램.
자세히 읽어보세요: 지수: 정의, 공식, 법칙 및 예
지수 규칙이란 무엇입니까?
지수 규칙은 지수 문제를 해결하는 데 사용되는 규칙입니다. 두 개의 지수가 주어졌다고 가정하자. 중 그리고 N 그리고 우리는 두 지수의 곱을 찾아야 합니다. 그런 다음 지수 규칙의 개념이나 지수의 곱 규칙을 사용합니다. 즉,
ㅏ 중 × N =a (m+n)
지수 문제를 해결하기 위해 다양한 다른 규칙이 사용됩니다. 이러한 규칙을 지수 규칙이라고 합니다.
이 지침은 소수 지수, 분수, 무리수 및 음의 정수를 사용하여 표현식을 단순화하는 데 도움이 됩니다.
지수의 법칙이란 무엇입니까?
지수의 법칙은 산술 문제를 쉽게 해결하는 데 도움이 되는 일련의 규칙입니다. 때때로 우리는 곱셈을 길게 만드는 큰 지수를 얻을 수 있기 때문에 지수 법칙의 도움으로 문제를 쉽고 시간 제한적으로 해결할 수 있습니다.
다음은 일곱 가지이다. 지수의 법칙 지수와 관련된 산술 문제를 해결하기 위해 알아야 할 사항:
- 거듭제곱 법칙의 산물
- 거듭제곱의 법칙
- 거듭제곱 법칙의 힘
- 거듭제곱 법칙의 힘
- 몫의 법칙의 거듭제곱
- 제로 전력 규칙
- 음수 지수 규칙
거듭제곱 법칙의 산물
에서 권력의 산물 규칙 , 밑이 같고 지수가 다른 두 숫자를 곱하면 밑의 지수가 추가되어 곱을 찾습니다. x로 표현됩니다 중 ×x N = x (m+n)
예: 5 2 ×5 삼 =?
밑값은 둘 다 5이므로 동일하게 유지한 다음 지수를 함께 더합니다(2+3).
5 2 ×5 삼 = 5 23 = 5 5
답을 얻으려면 5를 5번 곱하세요.
5 5 = 5 × 5 × 5 × 5 × 5 = 3125
거듭제곱의 법칙
~ 안에 거듭제곱의 몫 규칙 , 밑이 같고 지수가 다른 두 숫자를 나누면 밑의 지수를 빼서 몫을 찾습니다. x로 표현됩니다 ㅏ ¶x 비 = x (a-b)
예: 4 5 ¼ 4 삼 =?
해결책:
4 5 ¼ 4 삼 =?
이 방정식의 두 밑수는 모두 4이므로 동일하게 유지됩니다. 그런 다음 지수를 사용하여 피제수에서 제수를 뺍니다.
4 5 ¼ 4 삼 = 4 5-3 = 4 2
마지막으로, 필요한 경우 방정식을 단순화합니다.
4 2 = 4 × 4 = 16
거듭제곱 법칙의 힘
~ 안에 권력의 힘 규칙 , 어떤 거듭제곱으로 올린 숫자가 다시 어떤 거듭제곱으로 올라가면 두 거듭제곱이 곱해집니다. (x)로 표현된다. 중 ) N = x m×n
예: (2 삼 ) 2 =?
해결책:
(2 삼 ) 2 =?
밑수를 일정하게 유지하면서 위와 같은 방정식에서 지수를 함께 곱합니다.
2 3×2 = 2 6
하지만 , 우리는 ((2^3)^2 ~ eq~2^{3^2} 가 (2 와 같다는 것을 명심해야 합니다. 삼 ) 2 = 2 6 그러나 2^{3^2} = 2^9는 지수 3만 밑을 포함한 정수가 아닌 지수 2로 다시 증가하기 때문입니다.
제품 규칙의 힘
~ 안에 제품의 힘 규칙 , 두 개의 서로 다른 밑수에 동일한 거듭제곱을 곱한 다음 밑수를 곱하고 밑수 곱에 거듭제곱이 공통됩니다. (x)로 표현된다. 중 × 그리고 중 ) = (xy) 중 . 주어진 질문이 (xy)라면 중 그런 다음 밑수에 지수를 곱할 때 밑수의 각 부분에 지수를 분배하므로 (xy) 중 = (엑스 중 × 그리고 중 )
예: 2 삼 ×3 삼 =?
해결책:
밑수가 다르고 거듭제곱이 같으므로 밑수를 곱하여 공통 거듭제곱으로 올립니다.
그러므로 2 삼 ×3 삼 =(23) 삼 = 6 삼 = 216
예: (2×3) 삼 =?
해결책:
이 경우 동일한 전원을 개별 베이스에 분리합니다.
따라서 (2×3) 삼 = 2 삼 ×3 삼 = 8×27 = 216
몫의 법칙의 거듭제곱
~ 안에 몫의 법칙의 거듭제곱 , 동일한 거듭제곱을 갖는 두 개의 서로 다른 염기를 나누면 결과는 동일한 거듭제곱으로 올라간 염기의 몫입니다. 이는 x로 표시됩니다. 중 /그리고 중 = (x/y) 중 . 이 경우 그 반대도 마찬가지입니다. 즉, 분자와 분모 모두 동일한 거듭제곱으로 거듭제곱되면 거듭제곱은 분자와 분모 모두에 개별적으로 분배됩니다. (x/y)로 나타낼 수 있습니다. 중 = x 중 /그리고 중
예: 단순화 6 4 /삼 4 .
해결책:
이 경우, 밑의 몫을 구하고 그에 대한 공통 전력을 높이십시오.
6 4 /삼 4 = (6/3) 4 = 2 4 = 16
예: 단순화(6/3) 4 .
해결책:
이 경우에는 4의 거듭제곱을 분자와 분모 모두에 분배합니다.
(6/3) 4 = 6 4 /삼 4 = (6×6×6×6)/(3×3×3×3) = 2×2×2×2 = 16
제로 전력 규칙
~ 안에 제로 전력 규칙 , 어떤 밑이 0으로 거듭제곱되면 결과는 1이 됩니다. 이는 x로 표시될 수 있습니다. 0 = 1. 영전력 법칙은 다음 설명을 통해 이해할 수 있습니다.
x를 증명해야 한다고 가정하자. 0 = 1.
엑스 0 = x n-n , 여기서 (0 = n-n)
거듭제곱의 몫 규칙에서 우리는 밑이 동일하면 몫을 찾는 동안 지수를 뺍니다. 거듭제곱 법칙의 반대의 경우도 마찬가지입니다.
⇒ x n-n = x N /엑스 N = 1
따라서, x 0 = 1.
법을 더 잘 이해하기 위해 예를 들어 보겠습니다.
예: (1001) 0 =?
0의 거듭제곱 규칙에 따라 0의 거듭제곱으로 올림된 숫자는 값 1이 됩니다.
(1001) 0 = 1
음수 지수 규칙
~ 안에 음수 지수 규칙 , 숫자가 음수로 증가하면 밑수를 역수로 변환하고 거듭제곱은 양수로 변경됩니다. 그 반대의 경우도 마찬가지입니다. 즉, 지수가 양수이고 밑이 역수로 변환되면 지수가 음수 값으로 변경됩니다. (x/y)로 나타낼 수 있습니다. -중 = (y/x) 중
예: (2/3) -2 =?
해결책:
지수가 음수이므로 밑은 역수로 변환됩니다.
23) -2 = (3/2) 2 = 3 2 /2 2 = 9/4
분수 지수 규칙(분수를 포함한 지수의 법칙)
분수 지수 규칙은 분수 지수 또는 분수 형태의 지수를 풀 때 사용되는 규칙입니다. 분수 형식의 지수는 다음과 같이 작성됩니다. 1/n 그리고 a의 n번째 루트로 읽혀집니다. 또한 다음과 같이 표현됩니다.
ㅏ 1/n = N √(a)
여기서 a는 지수의 밑수이고 1/n은 분수 형식의 지수입니다.
예를 들어 (8)을 단순화합니다. 1/3
= (8) 1/3 = ∛(8)
= ∛(2×2×2)
= 2
기타 지수 규칙
위의 7가지 지수 법칙 외에도 다음은 지수 문제를 풀 때 명심해야 할 몇 가지 지수 법칙의 법칙입니다.
- 음수를 짝수로 올리면 결과는 양수가 되고 음수를 홀수로 올리면 결과는 항상 음수가 됩니다. 예를 들어 (-2) 4 = 16 및 (-2) 5 = -32.
- 1을 거듭제곱하면 결과는 항상 1이 됩니다. 예를 들어 1 삼 = 1, 1 1001 = 1.
- 1을 제외한 임의의 숫자를 무한대로 거듭제곱하면 결과는 무한대가 됩니다. 2 ∨ =
지수와 로그의 법칙
지수의 법칙과 로그의 법칙은 다양한 수학적 문제를 해결하는 데 사용되는 두 가지 규칙으로, 이 규칙을 아래 표에 추가했습니다.
| 규칙 | 지수 | 로그 |
|---|---|---|
| 제품 규칙 | 엑스 피 .엑스 큐 = x (p+q) | 통나무 ㅏ (mn) = 로그 ㅏ m + 로그 ㅏ N |
| 몫의 법칙 | 엑스 피 /엑스 큐 = x (p-q) | 통나무 ㅏ (m/n) = 로그 ㅏ m - 로그 ㅏ N |
| 권력의 법칙 | (엑스 피 ) 큐 = x p.q | 통나무 ㅏ mn = nlog ㅏ 중 |
표: 지수의 법칙
위에서 언급한 7가지 지수 법칙은 다음 표에 요약되어 있습니다.

사람들은 또한 읽습니다:
- 음수 지수
- 지수를 곱하고 나누는 방법
- 지수 더하기 및 빼기
- 실수에 대한 지수의 법칙
지수 규칙 예
예 1: 7을 단순화하면 무엇입니까? 삼 ×7 1 ?
해결책:
7 삼 ×7 1 = 7 3+1 = 7 4
예시 2: 단순화하여 10의 값 구하기 2 /5 2 .
해결책:
주어진 표현을 다음과 같이 쓸 수 있습니다.
10 2 /5 2 = (10/5) 2 = 2 2 = 4
예시 3: (256)의 값 찾기 3/4
해결책:
(256) 3/4 = (4 4 ) 3/4 = 4 4×(3/4) = 4 삼 = 64
예시 4: 7의 값 찾기 -삼
해결책:
7 -삼 = (1/7) 삼 = 1 삼 /7 삼 = 1/343
예제 5: 125 = 25/5인 경우 x 값 찾기 엑스
해결책:
125 = 25/5 엑스
⇒ 5 삼 = 5 2 /5 엑스
⇒ 5 삼 = 5 2-x
이제 양변의 수량이 동일하고 밑수도 동일하므로 지수도 동일합니다.
⇒ 3 = 2-x
⇒ x = 2-3 = -1
또한 확인하십시오:
- 지수 방정식
- 무리수
지수 규칙 – FAQ
수학에서 지수란 무엇입니까?
지수는 기본적으로 숫자에 거듭제곱과 동일한 횟수를 곱하는 것을 의미하는 숫자에 대한 거듭제곱을 나타냅니다.
거듭제곱 법칙의 곱은 무엇입니까?
거듭제곱의 법칙(Product of Power)은 동일한 밑수를 가진 두 숫자가 다른 숫자로 올림될 때 숫자의 곱이 두 숫자의 거듭제곱의 합과 동일한 거듭제곱을 갖게 된다는 것을 나타냅니다. x로 주어진다 중 × × N = x (m+n)
권력의 법칙이란 무엇입니까?
거듭제곱의 법칙은 숫자가 어떤 거듭제곱으로 올라가고 첫 번째 거듭제곱을 포함한 전체 숫자가 다시 어떤 거듭제곱으로 올라가면 두 거듭제곱이 곱해진다는 것입니다.
제로 지수 규칙이란 무엇입니까?
영 지수 규칙에 따르면 숫자가 0으로 거듭제곱되면 결과는 1이 됩니다. X로 표시됩니다. 0 = 1.
0의 가치는 무엇입니까 0 ?
0의 값 0 수학에서는 정의되지 않습니다.
지수의 8가지 법칙은 무엇인가요?
지수의 8법칙은 다음과 같습니다.
- 상품법: a 중 × N =a m+n
- 몫의 법칙: a 중 /ㅏ N =a m-n
- 영지수 법칙: a 0 = 1
- 항등지수 법칙: a 1 =a
- 힘의 힘: (a 중 ) N =a 백만
- 제품의 힘: (ab) 중 =a 중 비 중
- 몫의 거듭제곱: (a/b) 중 =a 중 /비 중
- 음의 지수 법칙: -중 = 1/a 중