K'th 붐 번호

GfG Practice에서 사용해 보세요.  #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; }
산출
 #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; } 붐 번호는 숫자 2와 3으로만 구성된 숫자입니다. 정수 k(0
Input : k = 2 Output: 3 Input : k = 3 Output: 22 Input : k = 100 Output: 322323 Input: k = 1000000 Output: 3332322223223222223Recommended Practice K번째 붐 번호 시도해 보세요!
아이디어는 다음과 같이 매우 간단합니다. 이진수 생성 . 여기서도 동일한 접근 방식을 사용합니다.
우리는 이 문제를 해결하기 위해 대기열 데이터 구조를 사용합니다. 먼저 '2'를 대기열에 넣은 다음 '3'을 입력합니다. 이 두 개는 각각 첫 번째 및 두 번째 붐 번호입니다. 이제 대기열 앞에 pop()할 때마다 count=2를 설정하고 팝된 숫자에 '2'를 추가하고 count++를 증가시킵니다. if (count==k) 그런 다음 현재를 인쇄합니다. 붐 번호 그렇지 않으면 팝된 숫자에 '3'을 추가하고 count++를 증가시킵니다. if (count==k) 그런 다음 현재를 인쇄합니다. 붐 번호 . K'th에 도달할 때까지 이 과정을 반복합니다. 붐 번호 .
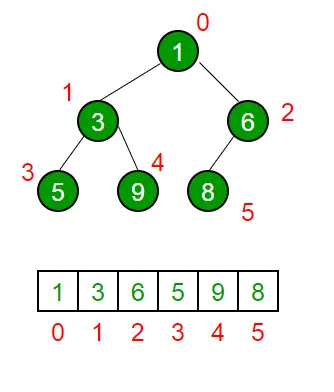
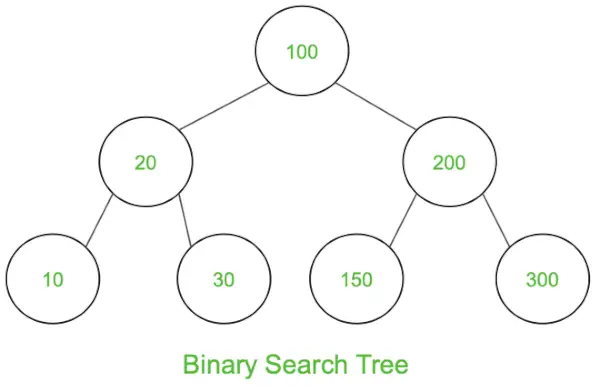
이 접근 방식은 루트가 빈 문자열인 트리의 BFS로 볼 수 있습니다. 모든 노드의 왼쪽 자식에는 2가 추가되고 오른쪽 자식에는 3이 추가됩니다.
아래는 이 아이디어를 구현한 것입니다.
C++ // C++ program to find K'th Boom number #include using namespace std ; typedef long long int ll ; // This function uses queue data structure to K'th // Boom number void boomNumber ( ll k ) { // Create an empty queue of strings queue < string > q ; // Enqueue an empty string q . push ( '' ); // counter for K'th element ll count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number string s1 = q . front (); // pop front q . pop (); // Store current Boom number before changing it string s2 = s1 ; // Append '2' to string s1 and enqueue it q . push ( s1 . append ( '2' )); count ++ ; // check if count==k if ( count == k ) { cout < < s1 < < endl ; // K'th Boom number break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front q . push ( s2 . append ( '3' )); count ++ ; // check if count==k if ( count == k ) { cout < < s2 < < endl ; // K'th Boom number break ; } } return ; } // Driver program to test above function int main () { ll k = 1000000 ; boomNumber ( k ); return 0 ; }
Java /*package whatever //do not write package name here */ import java.io.* ; import java.util.* ; class GFG { // This function uses queue data structure to K'th // Boom number static void boomNumber ( long k ) { // Create an empty queue of strings Queue < String > q = new LinkedList < String > (); // Enqueue an empty string q . add ( '' ); // counter for K'th element long count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number String s1 = q . poll (); // Store current Boom number before changing it String s2 = s1 ; // Append '2' to string s1 and enqueue it q . add ( s1 + '2' ); count ++ ; // check if count==k if ( count == k ) { System . out . println ( s1 ); // K'th Boom number break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front q . add ( s2 + '3' ); count ++ ; // check if count==k if ( count == k ) { System . out . println ( s2 ); // K'th Boom number break ; } } return ; } // Driver code public static void main ( String args [] ) { long k = 1000000 ; boomNumber ( k ); } } // This code is contributed by shinjanpatra
Python3 # Python3 program to find K'th Boom number # This function uses queue data structure to K'th # Boom number def boomNumber ( k ): # Create an empty queue of strings q = [] # Enqueue an empty string q . append ( '' ) # counter for K'th element count = 0 # This loop checks the value of count to # become equal to K when value of count # will be equals to k we will print the # Boom number while ( count <= k ): # current Boom number s1 = q [ 0 ] # pop front q = q [ 1 :] # Store current Boom number before changing it s2 = s1 # Append '2' to string s1 and enqueue it s1 += '2' q . append ( s1 ) count = count + 1 # check if count==k if ( count == k ): print ( s1 ) # K'th Boom number break # Append '3' to string s2 and enqueue it. # Note that s2 contains the previous front s2 += '3' q . append ( s2 ) count = count + 1 # check if count==k if ( count == k ): print ( s2 ) # K'th Boom number break return # Driver program to test above function k = 1000000 boomNumber ( k ) # This code is contributed by shinjanpatra
C# // C# program to find K'th Boom number using System ; using System.Collections ; class GFG { // This function uses queue data structure // to K'th Boom number static void boomNumber ( long k ) { // Create an empty queue of strings Queue q = new Queue (); // Enqueue an empty string q . Enqueue ( '' ); // counter for K'th element long count = 0 ; // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ) { // current Boom number string s1 = ( string ) q . Dequeue (); // Store current Boom number // before changing it string s2 = s1 ; // Append '2' to string s1 and // enqueue it s1 += '2' ; q . Enqueue ( s1 ); count ++ ; // Check if count==k if ( count == k ) { // K'th Boom number Console . Write ( s1 ); break ; } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front s2 += '3' ; q . Enqueue ( s2 ); count ++ ; // Check if count==k if ( count == k ) { // K'th Boom number Console . Write ( s2 ); break ; } } return ; } // Driver code public static void Main ( string [] arg ) { long k = 1000000 ; boomNumber ( k ); } } // This code is contributed by rutvik_56
JavaScript < script > // JavaScript program to find K'th Boom number // This function uses queue data structure to K'th // Boom number function boomNumber ( k ){ // Create an empty queue of strings let q = [] // Enqueue an empty string q . push ( '' ) // counter for K'th element let count = 0 // This loop checks the value of count to // become equal to K when value of count // will be equals to k we will print the // Boom number while ( count <= k ){ // current Boom number let s1 = q . shift () // Store current Boom number before changing it let s2 = s1 // Append '2' to string s1 and enqueue it s1 += '2' q . push ( s1 ) count = count + 1 // check if count==k if ( count == k ){ document . write ( s1 ' ' ) // K'th Boom number break } // Append '3' to string s2 and enqueue it. // Note that s2 contains the previous front s2 += '3' q . push ( s2 ) count = count + 1 // check if count==k if ( count == k ){ document . write ( s2 ' ' ) // K'th Boom number break } } return } // Driver program to test above function let k = 1000000 boomNumber ( k ) // This code is contributed by shinjanpatra < /script>
산출
3332322223223222223
시간 복잡도: O(K)
보조 공간: O(n)
이 기사는 GeeksforGeeks 팀에서 검토했습니다.