B-TREE 소개 - TECHCODEVIEW.COM

전통적인 이진 검색 트리의 한계는 실망스러울 수 있습니다. 대용량 데이터를 손쉽게 처리할 수 있는 다재다능한 데이터 구조, B-Tree를 만나보세요. 대량의 데이터를 저장하고 검색할 때 기존 이진 검색 트리는 성능이 낮고 메모리 사용량이 높아 실용적이지 않을 수 있습니다. B-트리(B-Tree) 또는 균형 트리(Balanced Tree)라고도 알려진 B-트리는 이러한 한계를 극복하기 위해 특별히 설계된 자체 균형 트리 유형입니다.

기존 이진 검색 트리와 달리 B-트리는 단일 노드에 저장할 수 있는 키의 수가 많기 때문에 대형 키 트리라고도 알려져 있습니다. B-트리의 각 노드에는 여러 개의 키가 포함될 수 있으며, 이를 통해 트리는 더 큰 분기 요소를 가지므로 더 낮은 높이를 가질 수 있습니다. 높이가 낮으면 디스크 I/O가 줄어들어 검색 및 삽입 작업이 더 빨라집니다. B-트리는 하드 드라이브, 플래시 메모리, CD-ROM과 같이 느리고 대용량 데이터 액세스가 가능한 스토리지 시스템에 특히 적합합니다.

B-트리는 각 노드에 최소 개수의 키가 있는지 확인하여 균형을 유지하므로 트리는 항상 균형을 유지합니다. 이러한 균형은 트리의 초기 모양에 관계없이 삽입, 삭제, 검색과 같은 작업의 시간 복잡도가 항상 O(log n)임을 보장합니다.

B-트리의 시간 복잡도:

아니요.	연산	시간 복잡도
1.	찾다	O(로그 n)
2.	끼워 넣다	O(로그 n)
삼.	삭제	O(로그 n)

메모: n은 B-트리의 총 요소 수입니다.

B-트리의 속성:

모든 잎은 같은 수준에 있습니다.
B-Tree는 최소 차수 '라는 용어로 정의됩니다. 티 '. 의 가치 ' 티 '는 디스크 블록 크기에 따라 다릅니다.
루트를 제외한 모든 노드에는 최소한 t-1개의 키가 포함되어야 합니다. 루트에는 최소한의 내용이 포함될 수 있습니다. 1 열쇠.
모든 노드(루트 포함)에는 최대( 2*티 – 1 ) 키.
노드의 자식 수는 해당 노드의 키 수에 더한 값과 같습니다. 1 .
노드의 모든 키는 오름차순으로 정렬됩니다. 두 키 사이의 자식 k1 그리고 k2 다음 범위의 모든 키를 포함합니다. k1 그리고 k2 .
B-트리는 이진 검색 트리와 달리 루트에서 성장하고 축소됩니다. 이진 검색 트리는 아래로 성장하고 아래로 축소됩니다.
다른 균형 이진 검색 트리와 마찬가지로 검색, 삽입, 삭제의 시간 복잡도는 O(log n)입니다.
B-Tree에 노드를 삽입하는 것은 Leaf Node에서만 발생합니다.

다음은 최소 차수가 5인 B-트리의 예입니다.
메모: 실제 B-트리에서는 최소 차수의 값이 5보다 훨씬 큽니다.

위 다이어그램에서 모든 리프 노드는 동일한 레벨에 있고 리프가 아닌 모든 노드에는 빈 하위 트리가 없으며 키가 자식 수보다 1 적은 것을 볼 수 있습니다.

B-나무에 대한 흥미로운 사실:

n개의 노드로 존재할 수 있는 B-트리의 최소 높이는 다음과 같습니다. m은 노드의 최대 자식 수입니다. $h_{분} =lceillog_m (n + 1) ceil - 1$

n개의 노드로 존재할 수 있는 B-트리의 최대 높이는 루트가 아닌 노드가 가질 수 있는 최소 하위 노드 수인 t입니다. $h_{최대} =lfloorlog_tfrac {n + 1}{2} floor$ 그리고 $t = lceilfrac {m}{2} ceil$

B-트리에서의 순회:

탐색은 이진 트리의 중위 탐색과도 유사합니다. 가장 왼쪽 자식부터 시작하여 가장 왼쪽 자식을 반복적으로 인쇄한 다음 나머지 자식과 키에 대해 동일한 프로세스를 반복합니다. 마지막으로 가장 오른쪽 자식을 재귀적으로 인쇄합니다.

B-트리에서의 검색 작업:

검색은 이진 검색 트리의 검색과 유사합니다. 검색할 키를 k로 둡니다.

루트에서 시작하여 재귀적으로 아래로 탐색합니다.
방문한 모든 리프가 아닌 노드에 대해
- 노드에 키가 있으면 간단히 노드를 반환합니다.
- 그렇지 않으면 노드의 적절한 자식(첫 번째 큰 키 바로 앞에 있는 자식)으로 되돌아갑니다.
리프 노드에 도달했지만 리프 노드에서 k를 찾지 못하면 NULL을 반환합니다.

B-트리를 검색하는 것은 이진 트리를 검색하는 것과 유사합니다. 알고리즘은 유사하며 재귀를 사용합니다. 각 수준에서 검색은 마치 키 값이 상위 범위에 존재하지 않고 키가 다른 분기에 존재하는 것처럼 최적화됩니다. 이러한 값은 검색을 제한하므로 제한 값 또는 분리 값이라고도 합니다. 리프 노드에 도달했는데 원하는 키를 찾지 못하면 NULL이 표시됩니다.

B-트리에서 요소를 검색하는 알고리즘:-

C++

struct> Node {> > int> n;> > int> key[MAX_KEYS];> > Node* child[MAX_CHILDREN];> > bool> leaf;> };> Node* BtreeSearch(Node* x,> int> k) {> > int> i = 0;> > while> (i n && k>x->키[i]) {> > i++;> > }> > if> (i n && k == x->키[i]) {> > return> x;> > }> > if> (x->잎) {> > return> nullptr;> > }> > return> BtreeSearch(x->자식[i], k);> }>

씨

BtreeSearch(x, k)> > i = 1> > > // n[x] means number of keys in x node> > while> i ? n[x] and k ? keyi[x]> > do> i = i + 1> > if> i n[x] and k = keyi[x]> > then> return> (x, i)> > if> leaf [x]> > then> return> NIL> > else> > return> BtreeSearch(ci[x], k)>

자바

class> Node {> > int> n;> > int> [] key => new> int> [MAX_KEYS];> > Node[] child => new> Node[MAX_CHILDREN];> > boolean> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i => 0> ;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

파이썬3

class> Node:> > def> __init__(> self> ):> > self> .n> => 0> > self> .key> => [> 0> ]> *> MAX_KEYS> > self> .child> => [> None> ]> *> MAX_CHILDREN> > self> .leaf> => True> def> BtreeSearch(x, k):> > i> => 0> > while> i and k>= x.key[i]: i += 1 if i and k == x.key[i]: return x if x.leaf: return None return BtreeSearch(x.child[i], k)>

씨#

class> Node {> > public> int> n;> > public> int> [] key => new> int> [MAX_KEYS];> > public> Node[] child => new> Node[MAX_CHILDREN];> > public> bool> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

자바스크립트

// Define a Node class with properties n, key, child, and leaf> class Node {> > constructor() {> > this> .n = 0;> > this> .key => new> Array(MAX_KEYS);> > this> .child => new> Array(MAX_CHILDREN);> > this> .leaf => false> ;> > }> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> > let i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }>

예:

입력: 주어진 B-Tree에서 120을 검색합니다.

해결책:

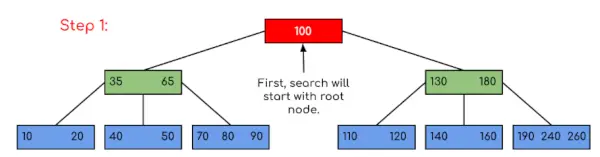
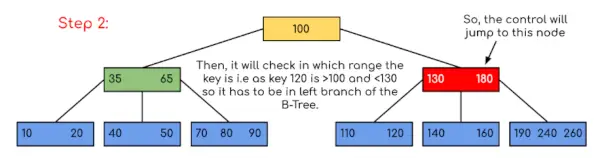
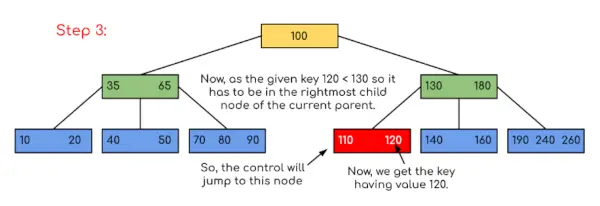
이 예에서는 값을 포함하는 키가 존재할 수 있는 가능성을 제한함으로써 검색이 감소했음을 알 수 있습니다. 마찬가지로 위의 예에서 180을 찾아야 한다면 프로그램이 키 180이 현재 노드 내에 존재한다는 것을 발견하기 때문에 제어는 2단계에서 중지됩니다. 마찬가지로 90을 찾는 경우 90 <100이므로 자동으로 왼쪽 하위 트리로 이동하므로 제어 흐름은 위의 예에 표시된 것과 유사하게 진행됩니다.

다음은 위의 접근 방식을 구현한 것입니다.

C++

// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> > int> * keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode** C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> public> :> > BTreeNode(> int> _t,> bool> _leaf);> // Constructor> > // A function to traverse all nodes in a subtree rooted> > // with this node> > void> traverse();> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode*> > search(> int> k);> // returns NULL if k is not present.> > // Make the BTree friend of this so that we can access> > // private members of this class in BTree functions> > friend> class> BTree;> };> // A BTree> class> BTree {> > BTreeNode* root;> // Pointer to root node> > int> t;> // Minimum degree> public> :> > // Constructor (Initializes tree as empty)> > BTree(> int> _t)> > {> > root = NULL;> > t = _t;> > }> > // function to traverse the tree> > void> traverse()> > {> > if> (root != NULL)> > root->트래버스();> > }> > // function to search a key in this tree> > BTreeNode* search(> int> k)> > {> > return> (root == NULL) ? NULL : root->검색(k);> > }> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(> int> _t,> bool> _leaf)> {> > // Copy the given minimum degree and leaf property> > t = _t;> > leaf = _leaf;> > // Allocate memory for maximum number of possible keys> > // and child pointers> > keys => new> int> [2 * t - 1];> > C => new> BTreeNode*[2 * t];> > // Initialize the number of keys as 0> > n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> > // There are n keys and n+1 children, traverse through n> > // keys and first n children> > int> i;> > for>

(i = 0; i   // If this is not leaf, then before printing key[i],  // traverse the subtree rooted with child C[i].  if (leaf == false)  C[i]->횡단();  시합 < < ' '  < < keys[i];  }  // Print the subtree rooted with last child  if (leaf == false)  C[i]->횡단(); } // 이 노드를 루트로 하는 하위 트리에서 키 k를 검색하는 함수 BTreeNode* BTreeNode::search(int k) { // k보다 크거나 같은 첫 번째 키를 찾습니다 int i = 0;  while (i 키[i]) i++;  // 찾은 키가 k와 같으면 이 노드를 반환합니다. if (keys[i] == k) return this;  // 여기에서 키를 찾을 수 없고 이것이 리프 노드인 경우 if (leaf == true) return NULL;  // 적절한 자식으로 이동 return C[i]->search(k); }>

자바

// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > System.out.println();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > boolean> > leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> boolean> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [> 2> * t -> 1> ];> > this> .C => new> BTreeNode[> 2> * t];> > this> .n => 0> ;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i => 0> ;> > for> (i => 0> ; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > System.out.print(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i => 0> ;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }>

파이썬3

# Create a node> class> BTreeNode:> > def> __init__(> self> , leaf> => False> ):> > self> .leaf> => leaf> > self> .keys> => []> > self> .child> => []> # Tree> class> BTree:> > def> __init__(> self> , t):> > self> .root> => BTreeNode(> True> )> > self> .t> => t> > # Insert node> > def> insert(> self> , k):> > root> => self> .root> > if> len> (root.keys)> => => (> 2> *> self> .t)> -> 1> :> > temp> => BTreeNode()> > self> .root> => temp> > temp.child.insert(> 0> , root)> > self> .split_child(temp,> 0> )> > self> .insert_non_full(temp, k)> > else> :> > self> .insert_non_full(root, k)> > # Insert nonfull> > def> insert_non_full(> self> , x, k):> > i> => len> (x.keys)> -> 1> > if> x.leaf:> > x.keys.append((> None> ,> None> ))> > while> i>> => 0> and> k[> 0>

] 0]:  x.keys[i + 1] = x.keys[i]  i -= 1  x.keys[i + 1] = k  else:  while i>= 0 및 k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # 자식 분할 def Split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] 그렇지 않은 경우 y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # 트리를 인쇄합니다 def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # 트리에서 검색 키 def search_key(self, k, x=None): x가 None이 아닌 경우: i = 0 while i x.keys[i][0]: i인 경우 += 1

씨#

// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > Console.WriteLine();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> bool> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [2 * t - 1];> > this> .C => new> BTreeNode[2 * t];> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i = 0;> > for> (i = 0; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > Console.Write(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > public> BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i = 0;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by Rajput-Ji>

자바스크립트

// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> > // Constructor (Initializes tree as empty)> > constructor(t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > > // function to traverse the tree> > traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > document.write(> ' '> );> > }> > > // function to search a key in this tree> > search(k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> > }> // A BTree node> class BTreeNode> {> > // Constructor> > constructor(t,leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> Array(2 * t - 1);> > this> .C => new> Array(2 * t);> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted with this node> > traverse()> > {> > // There are n keys and n+1 children, traverse through n keys> > // and first n children> > let i = 0;> > for> (i = 0; i <> this> .n; i++) {> > > // If this is not leaf, then before printing key[i],> > // traverse the subtree rooted with child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > document.write(keys[i] +> ' '> );> > }> > > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > > // A function to search a key in the subtree rooted with this node.> > search(k)> // returns NULL if k is not present.> > {> > > // Find the first key greater than or equal to k> > let i = 0;> > while> (i keys[i])> > i++;> > > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > > // If the key is not found here and this is a leaf node> > if> (leaf ==> true> )> > return> null> ;> > > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by patel2127>

메모: 위 코드에는 드라이버 프로그램이 포함되어 있지 않습니다. 다음 게시물에서는 전체 프로그램을 다룰 예정입니다. B-트리 삽입 .

B-트리를 정의하는 데에는 두 가지 규칙이 있습니다. 하나는 최소 차수로 정의하는 것이고, 두 번째는 순서로 정의하는 것입니다. 우리는 최소 학위 규칙을 따랐으며 B-Tree의 향후 게시물에서도 동일한 내용을 따를 것입니다. 위 프로그램에서 사용된 변수명 역시 동일하게 유지됩니다.