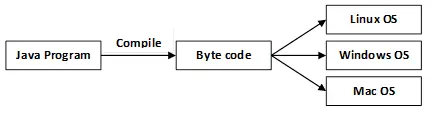
그래프에 대한 깊이 우선 검색 또는 DFS

깊이 우선 탐색(또는 DFS) 그래프는 다음과 비슷합니다. 트리의 깊이 우선 순회. 여기서 유일한 문제는 트리와 달리 그래프에 주기가 포함될 수 있다는 것입니다(노드를 두 번 방문할 수 있음). 노드를 두 번 이상 처리하지 않으려면 부울 방문 배열을 사용하십시오. 그래프에는 둘 이상의 DFS 순회가 있을 수 있습니다.
예:
그래프의 추천 실습 DFS 사용해 보세요!입력: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
산출: 정점 1의 DFS : 1 2 0 3
설명:
DFS 다이어그램:
실시예 1
입력: n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
산출: 정점 2의 DFS : 2 0 1 3
설명:
DFS 다이어그램:
실시예 2
DFS는 어떻게 작동하나요?
깊이 우선 검색은 트리 또는 그래프 데이터 구조를 순회하거나 검색하기 위한 알고리즘입니다. 알고리즘은 루트 노드(그래프의 경우 임의의 노드를 루트 노드로 선택)에서 시작하여 역추적하기 전에 각 분기를 따라 가능한 한 멀리 탐색합니다.
우리가 작동하는 것을 이해합시다 깊이 우선 검색 다음 그림의 도움으로:
1 단계: 처음에는 스택 및 방문한 배열이 비어 있습니다.
스택 및 방문 배열은 처음에는 비어 있습니다.
2 단계: 0을 방문하여 아직 방문하지 않은 인접 노드를 스택에 넣습니다.
노드 0을 방문하여 인접한 노드(1, 2, 3)를 스택에 넣습니다.
3단계: 이제 노드 1이 스택 상단에 있으므로 노드 1을 방문하여 스택에서 이를 팝하고 방문하지 않은 모든 인접 노드를 스택에 넣습니다.
노드 1 방문
4단계: 지금, 스택 맨 위에 있는 노드 2이므로 노드 2를 방문하여 스택에서 이를 팝하고 방문하지 않은 모든 인접 노드(예: 3, 4)를 스택에 넣습니다.
노드 2를 방문하고 방문하지 않은 인접 노드(3, 4)를 스택에 넣습니다.
5단계: 이제 노드 4가 스택 맨 위에 있으므로 노드 4를 방문하여 스택에서 이를 팝하고 방문하지 않은 모든 인접 노드를 스택에 넣습니다.
노드 4 방문
6단계: 이제 노드 3이 스택 맨 위에 있으므로 노드 3을 방문하여 스택에서 이를 팝하고 방문하지 않은 모든 인접 노드를 스택에 넣습니다.
노드 3 방문
이제 스택은 비어 있게 됩니다. 이는 모든 노드를 방문했고 DFS 순회가 종료되었음을 의미합니다.
다음은 위의 접근 방식을 구현한 것입니다.
C++
// C++ program to print DFS traversal from> // a given vertex in a given graph> #include> using> namespace> std;> // Graph class represents a directed graph> // using adjacency list representation> class> Graph {> public> :> > map <> int> ,> bool> >방문;> > map <> int> , list <> int> >> 조정;> > // Function to add an edge to graph> > void> addEdge(> int> v,> int> w);> > // DFS traversal of the vertices> > // reachable from v> > void> DFS(> int> v);> };> void> Graph::addEdge(> int> v,> int> w)> {> > // Add w to v’s list.> > adj[v].push_back(w);> }> void> Graph::DFS(> int> v)> {> > // Mark the current node as visited and> > // print it> > visited[v] => true> ;> > cout < < v < <> ' '> ;> > // Recur for all the vertices adjacent> > // to this vertex> > list <> int> >::반복자 i;> > for> (i = adj[v].begin(); i != adj[v].end(); ++i)> > if> (!visited[*i])> > DFS(*i);> }> // Driver code> int> main()> {> > // Create a graph given in the above diagram> > Graph g;> > g.addEdge(0, 1);> > g.addEdge(0, 2);> > g.addEdge(1, 2);> > g.addEdge(2, 0);> > g.addEdge(2, 3);> > g.addEdge(3, 3);> > cout < <> 'Following is Depth First Traversal'> > ' (starting from vertex 2)
'> ;> > // Function call> > g.DFS(2);> > return> 0;> }> // improved by Vishnudev C> |
자바
// Java program to print DFS traversal> // from a given graph> import> java.io.*;> import> java.util.*;> // This class represents a> // directed graph using adjacency> // list representation> class> Graph {> > private> int> V;> > // Array of lists for> > // Adjacency List Representation> > private> LinkedList adj[];> > // Constructor> > @SuppressWarnings> (> 'unchecked'> ) Graph(> int> v)> > {> > V = v;> > adj => new> LinkedList[v];> > for> (> int> i => 0> ; i adj[i] = new LinkedList(); } // Function to add an edge into the graph void addEdge(int v, int w) { // Add w to v's list. adj[v].add(w); } // A function used by DFS void DFSUtil(int v, boolean visited[]) { // Mark the current node as visited and print it visited[v] = true; System.out.print(v + ' '); // Recur for all the vertices adjacent to this // vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // The function to do DFS traversal. // It uses recursive DFSUtil() void DFS(int v) { // Mark all the vertices as // not visited(set as // false by default in java) boolean visited[] = new boolean[V]; // Call the recursive helper // function to print DFS // traversal DFSUtil(v, visited); } // Driver Code public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3); System.out.println( 'Following is Depth First Traversal ' + '(starting from vertex 2)'); // Function call g.DFS(2); } } // This code is contributed by Aakash Hasija> |
파이썬3
# Python3 program to print DFS traversal> # from a given graph> from> collections> import> defaultdict> # This class represents a directed graph using> # adjacency list representation> class> Graph:> > # Constructor> > def> __init__(> self> ):> > # Default dictionary to store graph> > self> .graph> => defaultdict(> list> )> > > # Function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > > # A function used by DFS> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > # and print it> > visited.add(v)> > print> (v, end> => ' '> )> > # Recur for all the vertices> > # adjacent to this vertex> > for> neighbour> in> self> .graph[v]:> > if> neighbour> not> in> visited:> > self> .DFSUtil(neighbour, visited)> > > # The function to do DFS traversal. It uses> > # recursive DFSUtil()> > def> DFS(> self> , v):> > # Create a set to store visited vertices> > visited> => set> ()> > # Call the recursive helper function> > # to print DFS traversal> > self> .DFSUtil(v, visited)> # Driver's code> if> __name__> => => '__main__'> :> > g> => Graph()> > g.addEdge(> 0> ,> 1> )> > g.addEdge(> 0> ,> 2> )> > g.addEdge(> 1> ,> 2> )> > g.addEdge(> 2> ,> 0> )> > g.addEdge(> 2> ,> 3> )> > g.addEdge(> 3> ,> 3> )> > print> (> 'Following is Depth First Traversal (starting from vertex 2)'> )> > > # Function call> > g.DFS(> 2> )> # This code is contributed by Neelam Yadav> |
씨#
// C# program to print DFS traversal> // from a given graph> using> System;> using> System.Collections.Generic;> // This class represents a directed graph> // using adjacency list representation> class> Graph {> > private> int> V;> > // Array of lists for> > // Adjacency List Representation> > private> List <> int> >[] 조정;> > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> List <> int> >[ ];> > for> (> int> i = 0; i adj[i] = new List |
자바스크립트
// Javascript program to print DFS> // traversal from a given> // graph> // This class represents a> // directed graph using adjacency> // list representation> class Graph> {> > > // Constructor> > constructor(v)> > {> > this> .V = v;> > this> .adj => new> Array(v);> > for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v, w) { // Add w to v's list. this.adj[v].push(w); } // A function used by DFS DFSUtil(v, visited) { // Mark the current node as visited and print it visited[v] = true; console.log(v + ' '); // Recur for all the vertices adjacent to this // vertex for(let i of this.adj[v].values()) { let n = i if (!visited[n]) this.DFSUtil(n, visited); } } // The function to do DFS traversal. // It uses recursive // DFSUtil() DFS(v) { // Mark all the vertices as // not visited(set as // false by default in java) let visited = new Array(this.V); for(let i = 0; i |
산출
Following is Depth First Traversal (starting from vertex 2) 2 0 1 3
깊이우선탐색의 복잡성 분석:
- 시간 복잡도: O(V + E), 여기서 V는 정점 수이고 E는 그래프의 간선 수입니다.
- 보조 공간: O(V + E), V 크기의 추가 방문 배열이 필요하고 DFS 함수에 대한 반복 호출을 위한 스택 크기가 필요합니다.








![텍사스 홍수로 머리까지 물이 차 집 앞에 사슬로 묶인 개 [구조 동영상]](https://techcodeview.com/img/trending/65/dog-chained-to-front-of-house-in-texas-flood-waters-up-to-her-head-rescue-video.webp)