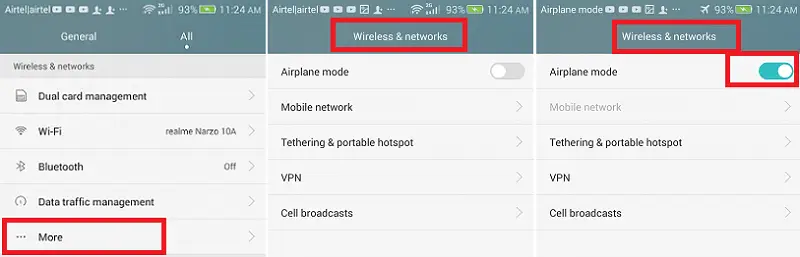
주어진 두 원이 서로 닿거나 교차하는지 확인

GfG Practice에서 사용해 보세요.  #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; }
산출
 #practiceLinkDiv { 표시: 없음 !중요; }
#practiceLinkDiv { 표시: 없음 !중요; } 중심이 있는 두 개의 원 A와 B가 있습니다. C1(x1y1) 그리고 C2(x2 y2) 반경 R1 그리고 R2 . 이 작업은 원 A와 B가 서로 닿는지 확인하는 것입니다.
예:
추천 연습 주어진 두 원이 서로 닿는지 확인해보세요.입력 : C1 = (3 4)
C2 = (14 18)
R1 = 5 R2 = 8
출력 : 원은 서로 닿지 않습니다.입력 : C1 = (2 3)
C2 = (15 28)
R1 = 12 R2 = 10
출력 : 원은 서로 교차합니다.입력 : C1 = (-10 8)
C2 = (14 -24)
R1 = 30 R2 = 10
접근하다:
중심 C1과 C2 사이의 거리는 다음과 같이 계산됩니다.
C1C2 = sqrt((x1 - x2) 2 + (y1 - y2) 2 ).
세 가지 조건이 발생합니다.
- 만약에 C1C2 <= R1 - R2: 원 B는 A 안에 있습니다.
- 만약에 C1C2 <= R2 - R1: 원 A는 B 안에 있습니다.
- 만약에 C1C2 < R1 + R2: 원은 서로 교차합니다.
- 만약에 C1C2 == R1 + R2: A와 B는 서로 연결되어 있습니다.
- 그렇지 않으면 원 A와 B는 겹치지 않습니다.
다음은 위의 접근 방식을 구현한 것입니다.
C++ // C++ program to check if two // circles touch each other or not. #include using namespace std ; int circle ( int x1 int y1 int x2 int y2 int r1 int r2 ) { double d = sqrt (( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 )); if ( d <= r1 - r2 ) { cout < < 'Circle B is inside A' ; } else if ( d <= r2 - r1 ) { cout < < 'Circle A is inside B' ; } else if ( d < r1 + r2 ) { cout < < 'Circle intersect to each other' ; } else if ( d == r1 + r2 ) { cout < < 'Circle touch to each other' ; } else { cout < < 'Circle not touch to each other' ; } } // Driver code int main () { int x1 = -10 y1 = 8 ; int x2 = 14 y2 = -24 ; int r1 = 30 r2 = 10 ; circle ( x1 y1 x2 y2 r1 r2 ); return 0 ; }
Java // Java program to check if two // circles touch each other or not. import java.io.* ; class GFG { static void circle ( int x1 int y1 int x2 int y2 int r1 int r2 ) { double d = Math . sqrt (( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 )); if ( d <= r1 - r2 ) { System . out . println ( 'Circle B is inside A' ); } else if ( d <= r2 - r1 ) { System . out . println ( 'Circle A is inside B' ); } else if ( d < r1 + r2 ) { System . out . println ( 'Circle intersect' + ' to each other' ); } else if ( d == r1 + r2 ) { System . out . println ( 'Circle touch to' + ' each other' ); } else { System . out . println ( 'Circle not touch' + ' to each other' ); } } // Driver code public static void main ( String [] args ) { int x1 = - 10 y1 = 8 ; int x2 = 14 y2 = - 24 ; int r1 = 30 r2 = 10 ; circle ( x1 y1 x2 y2 r1 r2 ); } } // This article is contributed by vt_m.
Python # Python program to check if two # circles touch each other or not. import math # Function to check if two circles touch each other def circle ( x1 y1 x2 y2 r1 r2 ): d = math . sqrt (( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 )) if ( d <= r1 - r2 ): print ( 'Circle B is inside A' ) elif ( d <= r2 - r1 ): print ( 'Circle A is inside B' ) elif ( d < r1 + r2 ): print ( 'Circle intersect to each other' ) elif ( d == r1 + r2 ): print ( 'Circle touch to each other' ) else : print ( 'Circle not touch to each other' ) # Driver code x1 y1 = - 10 8 x2 y2 = 14 - 24 r1 r2 = 30 10 # Function call circle ( x1 y1 x2 y2 r1 r2 ) # This code is contributed by Aman Kumar
C# // C# program to check if two // circles touch each other or not. using System ; class GFG { static void circle ( int x1 int y1 int x2 int y2 int r1 int r2 ) { double d = Math . Sqrt (( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 )); if ( d <= r1 - r2 ) { Console . Write ( 'Circle B is inside A' ); } else if ( d <= r2 - r1 ) { Console . Write ( 'Circle A is inside B' ); } else if ( d < r1 + r2 ) { Console . Write ( 'Circle intersect' + ' to each other' ); } else if ( d == r1 + r2 ) { Console . Write ( 'Circle touch to' + ' each other' ); } else { Console . Write ( 'Circle not touch' + ' to each other' ); } } // Driver code public static void Main ( String [] args ) { int x1 = - 10 y1 = 8 ; int x2 = 14 y2 = - 24 ; int r1 = 30 r2 = 10 ; circle ( x1 y1 x2 y2 r1 r2 ); } } // This article is contributed by Pushpesh Raj.
JavaScript // JavaScript program to check if two circles touch each other or not. function circle ( x1 y1 x2 y2 r1 r2 ) { var d = Math . sqrt (( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 )); if ( d <= r1 - r2 ) { console . log ( 'Circle B is inside A' ); } else if ( d <= r2 - r1 ) { console . log ( 'Circle A is inside B' ); } else if ( d < r1 + r2 ) { console . log ( 'Circle intersect to each other' ); } else if ( d === r1 + r2 ) { console . log ( 'Circle touch to each other' ); } else { console . log ( 'Circle not touch to each other' ); } } // Driver code var x1 = - 10 y1 = 8 ; var x2 = 14 y2 = - 24 ; var r1 = 30 r2 = 10 ; circle ( x1 y1 x2 y2 r1 r2 ); // this code is contributed by devendra
산출
Circle touch to each other
시간 복잡도: 내장된 sqrt 함수를 사용하기 때문에 O(log(n))
보조 공간: 오(1)
이 기사는 기고자: Aarti_Rathi 그리고 다르멘드라 쿠마르 .