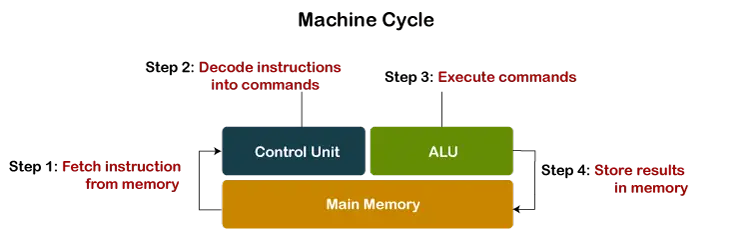
動的計画法を使用した巡回セールスマン問題

巡回セールスマン問題 (TSP):
一連の都市と各都市間の距離が与えられた場合、問題は、すべての都市を 1 回だけ訪れて開始点に戻る最短ルートを見つけることです。ハミルトニアンサイクルとTSPの違いに注目してください。ハミルトン サイクル問題は、すべての都市を正確に 1 回訪れるツアーが存在するかどうかを調べることです。ここで、ハミルトニアン ツアーが存在することがわかります (グラフが完成しているため)。実際、そのようなツアーは多数存在します。問題は、最小重みのハミルトニアン サイクルを見つけることです。

たとえば、右図のグラフを考えてみましょう。グラフのTSPツアーは1-2-4-3-1です。ツアーのコストは 10+25+30+15 で 80 です。問題は有名な NP 困難問題です。この問題に対する多項式時間の既知の解決策はありません。以下は、巡回セールスマン問題に対するさまざまな解決策です。
素朴な解決策:
1) 都市 1 を開始点と終了点として考えます。
2) (n-1) 個をすべて生成します。都市の順列。
3) すべての順列のコストを計算し、最小コストの順列を追跡します。
4) 最小コストの順列を返します。
時間計算量: ?(n!)
動的プログラミング:
指定された頂点のセットを {1, 2, 3, 4,....n} とします。 1 を出力の開始点と終了点として考えます。他のすべての頂点 I (1 以外) について、始点として 1、終点として I を使用し、すべての頂点が 1 回だけ出現する最小コスト パスを見つけます。このパスのコストをコスト (i) とし、対応するサイクルのコストをコスト (i) + dist(i, 1) とします。ここで、dist(i, 1) は I から 1 までの距離です。最後に、すべての [cost(i) + dist(i, 1)] 値の最小値。ここまでは簡単そうに見えます。
ここで問題は、cost(i) をどうやって取得するかということです。動的計画法を使用してコスト(i)を計算するには、部分問題に関して何らかの再帰関係が必要です。
用語を定義しましょう C(S, i) は、セット S 内の各頂点を 1 回だけ訪問し、1 から始まり i で終わる最小コスト パスのコストです。 。サイズ 2 のすべてのサブセットから始めて、S がサブセットであるすべてのサブセットの C(S, i) を計算し、次にサイズ 3 のすべてのサブセット S について C(S, i) を計算します。すべてのサブセットに 1 が存在する必要があることに注意してください。
If size of S is 2, then S must be {1, i}, C(S, i) = dist(1, i) Else if size of S is greater than 2. C(S, i) = min { C(S-{i}, j) + dis(j, i)} where j belongs to S, j != i and j != 1. 以下は、トップダウンの再帰的 + メモ化されたアプローチを使用した、問題に対する動的プログラミングの解決策です。
サブセットを維持するために、ビットマスクを使用してサブセット内の残りのノードを表すことができます。ビットの方が処理が速く、グラフ内のノードが少ないため、ビットマスクを使用する方が適しています。
例えば: -
10100 は、ノード 2 とノード 4 が処理されるためにセット内に残されていることを表します。
010010 は、ノード 1 と 4 がサブセットに残っていることを表します。
注: - グラフは 1 から始まるため、0 番目のビットは無視してください。
C++
#include> using> namespace> std;> // there are four nodes in example graph (graph is 1-based)> const> int> n = 4;> // give appropriate maximum to avoid overflow> const> int> MAX = 1000000;> // dist[i][j] represents shortest distance to go from i to j> // this matrix can be calculated for any given graph using> // all-pair shortest path algorithms> int> dist[n + 1][n + 1] = {> > { 0, 0, 0, 0, 0 }, { 0, 0, 10, 15, 20 },> > { 0, 10, 0, 25, 25 }, { 0, 15, 25, 0, 30 },> > { 0, 20, 25, 30, 0 },> };> // memoization for top down recursion> int> memo[n + 1][1 < < (n + 1)];> int> fun(> int> i,> int> mask)> > > // base case> > // if only ith bit and 1st bit is set in our mask,> > // it implies we have visited all other nodes already> > if> (mask == ((1 < < i)> // Driver program to test above logic> int> main()> {> > int> ans = MAX;> > for> (> int> i = 1; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = std::min(ans, fun(i, (1 < < (n + 1)) - 1)> > + dist[i][1]);> > printf> (> 'The cost of most efficient tour = %d'> , ans);> > return> 0;> }> // This code is contributed by Serjeel Ranjan> |
ジャワ
import> java.io.*;> import> java.util.*;> public> class> TSE {> > // there are four nodes in example graph (graph is> > // 1-based)> > static> int> n => 4> ;> > // give appropriate maximum to avoid overflow> > static> int> MAX => 1000000> ;> > // dist[i][j] represents shortest distance to go from i> > // to j this matrix can be calculated for any given> > // graph using all-pair shortest path algorithms> > static> int> [][] dist = {> > {> 0> ,> 0> ,> 0> ,> 0> ,> 0> }, {> 0> ,> 0> ,> 10> ,> 15> ,> 20> },> > {> 0> ,> 10> ,> 0> ,> 25> ,> 25> }, {> 0> ,> 15> ,> 25> ,> 0> ,> 30> },> > {> 0> ,> 20> ,> 25> ,> 30> ,> 0> },> > };> > // memoization for top down recursion> > static> int> [][] memo => new> int> [n +> 1> ][> 1> < < (n +> 1> )];> > static> int> fun(> int> i,> int> mask)> > > > // base case> > // if only ith bit and 1st bit is set in our mask,> > // it implies we have visited all other nodes> > // already> > if> (mask == ((> 1> < < i)> > // Driver program to test above logic> > public> static> void> main(String[] args)> > {> > int> ans = MAX;> > for> (> int> i => 1> ; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = Math.min(ans, fun(i, (> 1> < < (n +> 1> )) -> 1> )> > + dist[i][> 1> ]);> > System.out.println(> > 'The cost of most efficient tour = '> + ans);> > }> }> // This code is contributed by Serjeel Ranjan> |
Python3
n> => 4> # there are four nodes in example graph (graph is 1-based)> # dist[i][j] represents shortest distance to go from i to j> # this matrix can be calculated for any given graph using> # all-pair shortest path algorithms> dist> => [[> 0> ,> 0> ,> 0> ,> 0> ,> 0> ], [> 0> ,> 0> ,> 10> ,> 15> ,> 20> ], [> > 0> ,> 10> ,> 0> ,> 25> ,> 25> ], [> 0> ,> 15> ,> 25> ,> 0> ,> 30> ], [> 0> ,> 20> ,> 25> ,> 30> ,> 0> ]]> # memoization for top down recursion> memo> => [[> -> 1> ]> *> (> 1> < < (n> +> 1> ))> for> _> in> range> (n> +> 1> )]> def> fun(i, mask):> > # base case> > # if only ith bit and 1st bit is set in our mask,> > # it implies we have visited all other nodes already> > if> mask> => => ((> 1> < < i) |> 3> ):> > return> dist[> 1> ][i]> > # memoization> > if> memo[i][mask] !> => -> 1> :> > return> memo[i][mask]> > res> => 10> *> *> 9> # result of this sub-problem> > # we have to travel all nodes j in mask and end the path at ith node> > # so for every node j in mask, recursively calculate cost of> > # travelling all nodes in mask> > # except i and then travel back from node j to node i taking> > # the shortest path take the minimum of all possible j nodes> > for> j> in> range> (> 1> , n> +> 1> ):> > if> (mask & (> 1> < < j)) !> => 0> and> j !> => i> and> j !> => 1> :> > res> => min> (res, fun(j, mask & (~(> 1> < < i)))> +> dist[j][i])> > memo[i][mask]> => res> # storing the minimum value> > return> res> # Driver program to test above logic> ans> => 10> *> *> 9> for> i> in> range> (> 1> , n> +> 1> ):> > # try to go from node 1 visiting all nodes in between to i> > # then return from i taking the shortest route to 1> > ans> => min> (ans, fun(i, (> 1> < < (n> +> 1> ))> -> 1> )> +> dist[i][> 1> ])> print> (> 'The cost of most efficient tour = '> +> str> (ans))> # This code is contributed by Serjeel Ranjan> |
C#
using> System;> class> TSE> {> > // there are four nodes in example graph (graph is> > // 1-based)> > static> int> n = 4;> > // give appropriate maximum to avoid overflow> > static> int> MAX = 1000000;> > // dist[i][j] represents shortest distance to go from i> > // to j this matrix can be calculated for any given> > // graph using all-pair shortest path algorithms> > static> int> [, ] dist = { { 0, 0, 0, 0, 0 },> > { 0, 0, 10, 15, 20 },> > { 0, 10, 0, 25, 25 },> > { 0, 15, 25, 0, 30 },> > { 0, 20, 25, 30, 0 } };> > // memoization for top down recursion> > static> int> [, ] memo => new> int> [(n + 1), (1 < < (n + 1))];> > static> int> fun(> int> i,> int> mask)> > 3))> > return> dist[1, i];> > > // memoization> > if> (memo[i, mask] != 0)> > return> memo[i, mask];> > int> res = MAX;> // result of this sub-problem> > // we have to travel all nodes j in mask and end the> > // path at ith node so for every node j in mask,> > // recursively calculate cost of travelling all> > // nodes in mask> > // except i and then travel back from node j to node> > // i taking the shortest path take the minimum of> > // all possible j nodes> > for> (> int> j = 1; j <= n; j++)> > if> ((mask & (1 < < j)) != 0 && j != i && j != 1)> > res = Math.Min(res,> > fun(j, mask & (~(1 < < i)))> > + dist[j, i]);> > return> memo[i, mask] = res;> > > > // Driver program to test above logic> > public> static> void> Main()> > {> > int> ans = MAX;> > for> (> int> i = 1; i <= n; i++)> > // try to go from node 1 visiting all nodes in> > // between to i then return from i taking the> > // shortest route to 1> > ans = Math.Min(ans, fun(i, (1 < < (n + 1)) - 1)> > + dist[i, 1]);> > Console.WriteLine(> > 'The cost of most efficient tour = '> + ans);> > }> }> // This code is contributed by Tapesh(tapeshdua420)> |
JavaScript
> // JavaScript code for the above approach> > // there are four nodes in example graph (graph is 1-based)> > let n = 4;> > > // give appropriate maximum to avoid overflow> > let MAX = 1000000;> > // dist[i][j] represents shortest distance to go from i to j> > // this matrix can be calculated for any given graph using> > // all-pair shortest path algorithms> > let dist = [> > [0, 0, 0, 0, 0], [0, 0, 10, 15, 20],> > [0, 10, 0, 25, 25], [0, 15, 25, 0, 30],> > [0, 20, 25, 30, 0],> > ];> > // memoization for top down recursion> > let memo => new> Array(n + 1);> > for> (let i = 0; i memo[i] = new Array(1 < < (n + 1)).fill(0) } function fun(i, mask) // base case // if only ith bit and 1st bit is set in our mask, // it implies we have visited all other nodes already if (mask == ((1 < < i) // Driver program to test above logic let ans = MAX; for (let i = 1; i <= n; i++) // try to go from node 1 visiting all nodes in // between to i then return from i taking the // shortest route to 1 ans = Math.min(ans, fun(i, (1 < < (n + 1)) - 1) + dist[i][1]); console.log('The cost of most efficient tour ' + ans); // This code is contributed by Potta Lokesh> |
出力
The cost of most efficient tour = 80
時間計算量 : O(n 2 ※2 n ) ここで、O(n* 2 n) は、一意のサブ問題/状態の最大数と、各状態の遷移 (コードのように for ループによる) の O(n) です。
補助スペース:O(n*2 n )、 ここで、n はノード/シティの数です。
サイズ n のセットの場合、すべてのサブセットに n 番目が含まれないように、それぞれサイズ n-1 の n-2 個のサブセットを考慮します。上記の漸化関係を使用すると、動的計画ベースのソリューションを作成できます。最大でも O(n*2 n ) サブ問題があり、それぞれを解決するには直線的な時間がかかります。したがって、合計実行時間は O(n 2 ※2 n )。時間計算量は O(n!) よりもはるかに小さいですが、それでも指数関数的です。必要なスペースも指数関数的に増加します。したがって、このアプローチは、頂点の数がわずかに多い場合でも実行できません。巡回セールスマン問題の近似アルゴリズムについては間もなく説明します。
次の記事: 巡回セールスマン問題 |セット2
参考文献:
http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf
http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf