適合率と再現率の曲線 | ML - TECHCODEVIEW.COM

分類器のパフォーマンスを評価する方法は数多くあります。この記事では、適合率-再現率曲線を紹介し、適合率-再現率 (PR) 曲線と再現率 (PR) 曲線という 2 つの一般的なパフォーマンスレポート方法の違いをさらに詳しく調べます。受信機動作特性 (ROC) 曲線。 ROC 曲線についてはすでに説明されています。記事。適合率-再現率曲線とは何かを簡単に理解しましょう。

精度と再現率とは何ですか?

精度

すべての予測陽性観測値に対する正しく予測された陽性観測値の比率は、精度として知られています。
これは、モデルがどの程度良好な結果を予測するかを評価します。
精度の計算式は次のとおりです。

Precision = frac{True Positives}{True Positives + False Positives}

精度は、肯定的な予測の品質に関係します。精度が高いということは、モデルの誤検知率が低いことを示します。

想起

実際の陽性観察の総数に対する、正しく予測された陽性観察の比率は再現率として知られています。
これは、モデルが関連する各インスタンスをどの程度うまくキャプチャできるかを評価します。
再現率は次の式を使用して計算されます。

Precision = frac{True Positives}{True Positives + False Negatives}

再現率は、モデルによってキャプチャされた関連インスタンスの量に関係します。高い再現率は、モデルの偽陰性率が低いことを示します。

経験的解釈の観点から見ると、4 つの必須用語で構成される混同行列は、精度と再現率を理解するのに最も役立つツールです。

True Positive (TP): 正確に識別されたポジティブクラスインスタンスの数
False Positive (FP): 誤ってポジティブクラスインスタンスとして識別されるネガティブクラスインスタンスの数は、False Positive (FP) として知られています。
True Negative (TN): 正確に識別されたネガティブクラスインスタンスの数
False Negative (FN): 誤ってネガティブクラスインスタンス (False Negative、または FN) として分類されたポジティブクラスインスタンスの数。

機械学習における適合率-再現率 (PR) 曲線

精度の割合です 正しい 陽性分類（真陽性）を総数で割った値 予測された 行われた陽性分類 (真陽性 + 偽陽性)。想起の割合です 正しい 陽性分類 (真陽性) を合計数で割った値 本当に 陽性分類 (真陽性 + 偽陰性)。

PR 曲線は、Y 軸に精度値、X 軸に再現率値を示す単純なグラフです。言い換えると、PR 曲線には次のものが含まれます。 frac{TP}{TP+FP} y 軸上と frac{TP}{TP+FN} X 軸上。

精度は陽性的中率 (PPV) とも呼ばれることに注意することが重要です。
リコールは、感度、ヒット率、または真陽性率 (TPR) とも呼ばれます。

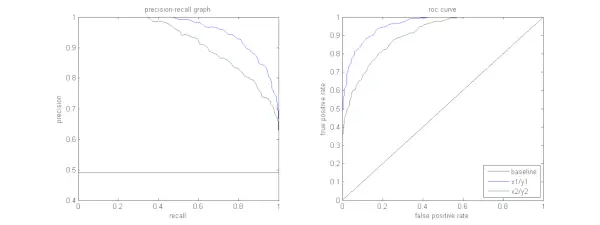
以下の図は、サンプルの PR 曲線と ROC 曲線の比較を示しています。

適合率-再現率曲線の解釈

アルゴリズムは高精度と高再現性の両方を備えていることが望まれます。ただし、ほとんどの機械学習アルゴリズムでは、多くの場合、この 2 つの間のトレードオフが関係します。優れた PR 曲線は、 AUC (曲線下面積) 。上の図では、青い線に対応する分類器のパフォーマンスが緑の線に対応する分類器よりも優れています。分類器の AUC が高いことに注意することが重要です。 ROC曲線 PR 曲線上の AUC も常に高くなります。ドキュメントがスポーツニュースのカテゴリに属するかどうかを分類するアルゴリズムを考えてみましょう。次のグラウンドトゥルース (実際の) ラベルと分類子出力クラスラベルを持つ 12 個のドキュメントがあると仮定します。

文書ID	グラウンドトゥルース	分類子の出力
D1	スポーツ	スポーツ
D2	スポーツ	スポーツ
D3	スポーツではない	スポーツ
D4	スポーツ	スポーツではない
D5	スポーツではない	スポーツではない
D6	スポーツ	スポーツではない
D7	スポーツではない	スポーツ
D8	スポーツではない	スポーツではない
D9	スポーツではない	スポーツではない
D10	スポーツ	スポーツ
D11	スポーツ	スポーツ
D12	スポーツ	スポーツではない

ここで、TP、TN、FP、FN の値を求めてみましょう。

分類における真陽性 (TP)、真陰性 (TN)、偽陽性 (FP)、および偽陰性 (FN) の定義をわかりやすく説明するために、スポーツまたは非スポーツとして分類されたドキュメントを含む例を使用してみましょう。

真陽性 (TP): スポーツとして正確に分類され、実際にスポーツに関する文書。このシナリオのドキュメント D1、D2、D10、および D11 は TP のインスタンスです。

真陰性 (TN): True Negative とは、スポーツとは何の関係もないにもかかわらず、ドキュメントに適切に「スポーツではない」というラベルが付けられたケースを指します。この例では、TN は文書 D5、D8、および D9 によって実証されています。

誤検知 (FP): スポーツとまったく関係がないにもかかわらず、誤ってスポーツとして分類された文書。ここにいくつかの FP の例、文書 D3 と D7 があります。

偽陰性 (FN): 誤って「スポーツではない」とラベル付けされた文書の例ですが、実際にはスポーツに関するものでした。この場合の文書 D4、D6、および D12 は FN の例です。

これらのカウントを考慮すると、次のようになります。市 =4、 テネシー州 =3、 FP =2、 FN =3

最後に、適合率と再現率は次のように計算されます。

Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}

Recall = frac{TP}{TP+FN} = frac{4}{7}

精度が 2/3 の場合、再現率は 4/7 ということになります。言い換えると、陽性と予想されたすべての症例のうち 3 分の 2 が正確に分類され (精度)、実際に陽性であったすべての症例のうち、モデルは 7 分の 4 を捕捉できました (再現率)。

異なるしきい値を設定すると、そのような精度と再現率のペアが複数得られます。このような P-R ペアを 0 から 1 の範囲の値で複数プロットすると、PR 曲線が得られます。

ROC 曲線が存在する場合、PR 曲線は必要ですか?

PR 曲線は、情報検索結果のレポートに特に役立ちます。
情報検索には、ドキュメントのプールを検索して、特定のユーザーのクエリに関連するドキュメントを見つけることが含まれます。たとえば、ユーザーが「ピンクの象」という検索クエリを入力したとします。検索エンジンは、数百万のドキュメントを (いくつかの最適化されたアルゴリズムを使用して) ざっと調べて、少数の関連ドキュメントを取得します。したがって、ノーであると安全に想定できます。関連文書の数は、その数に比べてはるかに少なくなります。無関係な文書の。

このシナリオでは、

TP = 検索された関連するドキュメントの数 (良好な結果)。
FP = 取得された関連性のないドキュメント (偽の検索結果) の数。
TN = 関連性がなく、取得されなかったドキュメントの数。
FN = 関連するが取得されなかったドキュメント (見逃した良好なドキュメント) の数。

ROC 曲線は、Recall = TPR = を含むプロットです。 frac{TP}{TP+FN} X 軸と FPR = frac{FP}{FP+TN} y 軸上。いいえ以来。真の陰性、つまり関連性がなく検索されなかった文書の数が非常に膨大なため、FPR は無視できるほど小さくなります。

さらに、FPR は、取得されていないドキュメントではなく、取得されたドキュメントに重点を置きたいため、検索システムを適切に評価するのには役立ちません。 PR 曲線はこの問題の解決に役立ちます。 PR 曲線の x 軸はリコール値 (TPR) であり、精度 = frac{TP}{TP+FP} y 軸上。正確さは強調点に役立ちます 取得された結果がどの程度関連しているか 、IRシステムを判断する際には、これがより重要です。したがって、PR 曲線は情報検索に関連する問題でよく見られます。

ROC 対適合率-再現率曲線をいつ使用するか?

ROC (受信者動作特性) 曲線は、クラス分布のバランスが取れている場合に適しており、偽陽性と偽陰性が同様の結果をもたらします。これらは、感度と特異性の間のトレードオフを示しています。対照的に、不均衡なデータセットを扱う場合は、正のクラス予測パフォーマンスに重点を置き、精度-再現率曲線が適しています。

Precision-Recall は、陽性例を正しく分類するモデルの能力についての洞察を提供します。 ROC と Precision-Recall のどちらを選択するかは、問題の特定のニーズに依存し、データの分布とさまざまな種類のエラーの結果を理解することが重要です。

適合率-再現率曲線の基本的なコード実装

必要なライブラリのインポート

これらのコード行は、 Python ライブラリおよび適合率-再現率曲線を生成するために必要なモジュールサイエンスキットの学習そして結果を視覚化しますマットプロットリブ。 Matplotlib は人気のある Python プロットライブラリであり、pyplot はさまざまな種類のプロットやチャートを作成するための簡単なインターフェイスを提供します。ロジスティック回帰は、バイナリおよびマルチクラス分類タスク用の一般的な分類アルゴリズムです。適合率と再現率の曲線と AUC は、一般的な評価指標です。二項分類特に不均衡なデータセットを扱う場合に問題が発生します。

Python3

 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc>

使用されるデータセット

このコードは、sci-kit-learn の「make_classification」関数を使用して、バイナリ分類問題の合成データセットを生成します。

Python3

 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)>

トレーニングとテストの分割

の train_test_split このコードスニペットでは、scikit-learn の関数を使用して、以前に生成された合成データセット (X および y) をトレーニングセットとテストセットに分割します。この分割は、機械学習モデルを評価する際の重要なステップです。モデルは、X_test および y_test データでテストされる前に、X_train および y_train データでトレーニングされ、未確認のサンプルでどの程度うまく機能するかを確認します。 train_test_split 関数はトレーニングセットとテストセットを分離し、モデルのパフォーマンスが新しい、これまでに見たことのないデータへの一般化を確実に反映するようにします。

Python3

 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)>

モデル構築

ここでは、ロジスティック回帰を使用してトレーニングデータセットでモデルをトレーニングしています。二値分類の一般的なアルゴリズムであるロジスティック回帰は、sci-kit-learn クラス LogisticRegression によって実装されます。

Python3

 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)>

モデル予測

通常、これらの計算により、さまざまな決定しきい値の適合率と再現率の値が得られます。これを使用して、適合率と再現率の曲線を描いたり、さまざまな時点での適合率と再現率の相対的な重要性を調べたりすることができます。そして計算すると、曲線下の面積 (AUC) 適合率-再現率曲線。

Python3

 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)>

PR 曲線のプロット

このコードブロックは、適合率と再現率の曲線を視覚化するための標準的な方法を提供し、さまざまな決定しきい値で適合率と再現率のトレードオフを評価できます。適合率-再現率曲線におけるモデルの全体的なパフォーマンスは、凡例に示されている AUC スコアによって要約されます。

Python3

 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()>

出力 :

適合率-再現率曲線

よくある質問 (FAQ)

Q. 精度とは何ですか?

予測された陽性の総数に対する正確に予測された陽性の観測値の比率は、精度として知られています。これは、モデルが肯定的な結果をどの程度予測しているかを評価します。精度の公式は次のとおりです。

Precision = frac{True Positives}{True Positives + False Positives}

Q. リコールとは何ですか?

再現率は、実際の陽性の総数に対する、正しく予測された陽性の観察の比率です。感度または真陽性率とも呼ばれます。モデルが関連する各インスタンスをどの程度うまくキャプチャできるかを評価します。再現率は次の式を使用して計算されます。

Precision = frac{True Positives}{True Positives + False Negatives}

Q. 精度と再現率が必要なのはなぜですか?

バイナリおよびマルチクラス分類問題における分類器のパフォーマンスを評価するには、精度と再現率という 2 つの評価指標が使用されます。陽性予測の精度は精度によって測定され、陽性予測の完全性は再現率によって測定されます。

Q. リコールと精度のトレードオフは何ですか?

再現率と精度はトレードオフの関係にあることがよくあります。精度が上がると再現率が低下する可能性があり、その逆も同様です。ポジティブなインスタンスを識別するためのバーを変更することで、このトレードオフを管理できます。逆に、しきい値が低いと再現率は低くなりますが、精度は高くなります。再現率と精度の間の決定は、特定の問題の詳細に基づいて行われます。

Q. F1 スコアとは何ですか? それは精度と再現率にどのように関係しますか?

再現率と適合率の調和平均は、F1 スコアとして知られています。偽陽性と偽陰性の両方を考慮した公平な測定を提供します。 F1 スコアは次の式を使用して計算されます。

F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall}

F1 スコアは、精度と再現率のバランスが崩れており、両者のバランスが必要な場合に特に役立ちます。