平面グラフ:

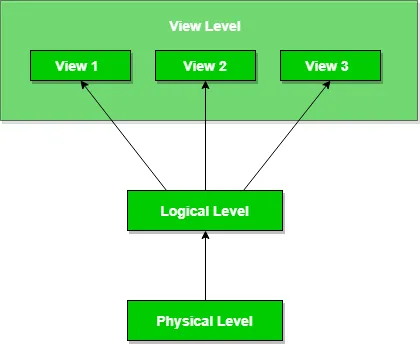
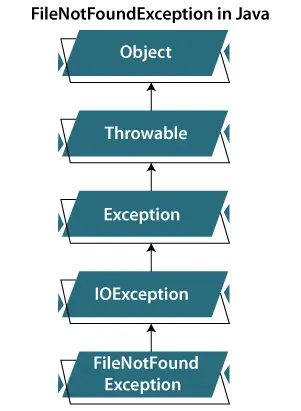
エッジが交差しないようにグラフを平面上に描画できる場合、そのグラフは平面的であると言われます。
例: 図に示すグラフは平面グラフです。


グラフの領域: 平面グラフ G=(V,E) を考えてみましょう。領域は、エッジによって境界が定められ、それ以上細分化できない平面の領域として定義されます。平面グラフは、計画を 1 つ以上の領域に分割します。これらの領域の 1 つは無限になります。
有限領域: 領域の面積が有限である場合、その領域は有限領域と呼ばれます。
無限領域: 領域の面積が無限である場合、その領域は無限領域と呼ばれます。平面グラフには無限領域が 1 つだけあります。
例: 図に示すグラフを考えてください。領域、有限領域、無限領域の数を決定します。

解決: 上のグラフには 5 つの領域があります。 1 、r 2 、r 3 、r 4 、r 5 。
グラフには 4 つの有限領域があります。つまり、r 2 、r 3 、r 4 、r 5 。
有限領域は 1 つだけ、つまり r だけです。 1
平面グラフのプロパティ:
- 接続された平面グラフ G に e 個のエッジと r 個の領域がある場合、r ≦
 そうです。
そうです。 - 接続された平面グラフ G に e 個のエッジ、v 個の頂点、および r 個の領域がある場合、v-e+r=2 になります。
- 接続された平面グラフ G に e 個のエッジと v 個の頂点がある場合、3v-e≧6 になります。
- 完全なグラフ K n n の場合にのみ平面です。 <5. < li>
- 完全な 2 部グラフ K ん m3 の場合にのみ平面です。
例: 完全なグラフ K を証明します。 4 平面的です。
解決: 完全なグラフ K 4 4 つの頂点と 6 つのエッジが含まれます。
接続された平面グラフの場合、3v-e≧6 であることがわかっています。したがって、K についても同様です。 4 とすると、性質(3)を満たす 3x4-6=6 が得られます。
したがって、K 4 は平面グラフです。したがって、証明されました。
非平面グラフ:
エッジが交差しないようにグラフを平面上に描画できない場合、グラフは非平面的であると言われます。
例: 図に示されているグラフは非平面グラフです。

これらのグラフは、エッジが交差しないように平面に描くことができないため、非平面グラフになります。
非平面グラフのプロパティ:
グラフが非平面であるのは、K と同相の部分グラフが含まれている場合に限ります。 5 またはK 3.3
例1: K を示してください 5 非平面的です。
解決: 完全なグラフ K 5 5 つの頂点と 10 のエッジが含まれます。
さて、接続された平面グラフの場合、3v-e≧6。
したがって、K については、 5 、 3 x 5-10=5 になります (これは 6 以上でなければならないため、プロパティ 3 を満たしません)。
したがって、K 5 は非平面グラフです。
例2: K と同相の部分グラフを見つけることによって、図に示されているグラフが非平面であることを示します。 5 またはK 3.3 。


解決: エッジを削除すると (V 1 、で 4 )、(で 3 、で 4 ) と (V 5 、で 4 ) グラフ G 1 ,K と同相となる 5 .したがって、それは非平面です。
エッジ V を削除すると 2,V 7) グラフG 2 Kと同型になる 3.3 .したがって、それは非平面です。
グラフの色付け:
G= (V,E) が複数のエッジを持たないグラフであると仮定します。 G の頂点カラーリングは、隣接する頂点が異なる色を持つように G の頂点に色を割り当てることです。 M-Colorsを使用するGのカラーリングが存在する場合、グラフGはM-Colorableです。
適切な色付け: 隣接する 2 つの頂点 u と v の色が異なる場合、そのカラーリングは適切です。そうでない場合は、不適切なカラーリングと呼ばれます。
例: 次のグラフを考えて、C={r, w, b, y} に色を付けます。すべての色またはより少ない色を使用してグラフを適切に色付けします。

図に示すグラフは最小 3 色であるため、x(G)=3
解決: 図は、4 つの色すべてで適切に色付けされたグラフを示しています。

図は、3 つの色で適切に色分けされたグラフを示しています。

Gの彩色番号: グラフ G の適切な色を生成するために必要な最小色の数は G の色数と呼ばれ、x(G) で表されます。
例: Kの彩色数 n nです。
解決: Kのぬりえ n 各頂点に異なる色を割り当てることで、n 色を使用して構築できます。このグラフの 2 つの頂点はすべて隣接しているため、2 つの頂点に同じ色を割り当てることはできません。したがって、Kの彩色数は n =n。
グラフの色分けの応用
グラフの色分けには次のような応用例があります。
- レジスタの割り当て
- 地図のぬりえ
- 二部グラフのチェック
- モバイル無線周波数の割り当て
- タイムテーブルの作成など。
ハンドシェイク定理を述べて証明します。
ハンドシェイク定理: グラフ G 内のすべての頂点の次数の合計は、グラフ内のエッジの数の 2 倍に等しくなります。
数学的には次のように言えます。
∑ v∈V 度(v)=2e
証拠: G = (V, E) を V = {v であるグラフとする 1 、で 2 、。 。 。 。 。 。 。 。 。 .} は頂点のセットであり、E = {e 1 、それは 2 。 。 。 。 。 。 。 。 。 .} はエッジのセットになります。すべてのエッジは 2 つの頂点の間にあるため、各頂点に次数 1 が与えられることがわかっています。したがって、各エッジはグラフの次数 2 に寄与します。したがって、すべての頂点の次数の合計は、G のエッジ数の 2 倍に等しくなります。
したがって、∑ v∈V 度(v)=2e