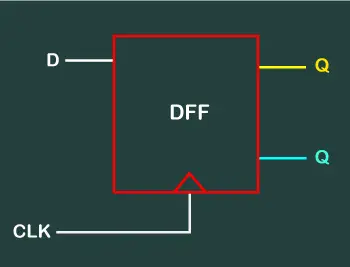
メイソンのゲイン公式

シグナル フロー グラフの入力変数と出力変数の間の関係は、メイソンのゲイン公式によって与えられます。
システム全体を決定するため、ゲインは次の式で求められます。

どこ、
P k = K の順方向パス ゲイン 番目 前進する道。
Δ = 1 - [すべての個別ループのループ ゲインの合計] + [2 つの非接触ループの可能なすべてのゲイン積の合計] + [可能なすべての 3 つの非接触ループのゲイン積の合計] + ... ....
Δ k = グラフのパスの Δ の値は、K に触れていないグラフの部分です。 番目 前進する道。

順方向パス
上記の SFG から、パス ゲインが次のような 2 つの順方向パスがあります。

ループ
上記の SFG には 5 つの個別のループがあり、そのループ ゲインは -

非接触ループ
非接触ループとループ ゲイン積の可能な組み合わせは 2 つあります。

上記の SFG では、3 つの非接触ループ、4 つの非接触ループなどの組み合わせは存在しません。
どこ、


例
シグナルフロー図を描き、図に示すブロック図の C/R を決定します。

上図のシグナルフローグラフを以下に描きます。

順方向パスのゲイン
P 1 =G 1 G 2 G 3 Δ 1 = 1
P 2 = -G 1 G 4 Δ 2 = 1
個々のループ
L 1 = -G 1 G 2 H 1
L 2 = -G 2 G 3 H 2
L 3 = -G 1 G 2 G 3
L 4 =G 1 G 4
L 5 =G 4 H 2
非接触ループ = 0








![軍事力別世界最強国トップ10 [2023]](https://techcodeview.com/img/current-gk/40/top-10-most-powerful-country-world-military-strength.webp)