LUHN アルゴリズム - TECHCODEVIEW.COM

Luhn アルゴリズムは、 モジュラス10 または 10に向かって アルゴリズムは、クレジットカード番号、IMEI 番号、カナダの社会保険番号など、さまざまな識別番号を検証するために使用される単純なチェックサム式です。 LUHN 公式は、1960 年代後半に数学者のグループによって作成されました。その後すぐに、クレジットカード会社がこれを採用しました。アルゴリズムはパブリックドメインにあるため、誰でも使用できます。ほとんどのクレジットカードと政府の識別番号の多くは、有効な番号とタイプミスや不正な番号を区別する簡単な方法としてこのアルゴリズムを使用しています。悪意のある攻撃ではなく、偶発的なエラーから保護するように設計されています。

Luhn アルゴリズムに含まれる手順

例を挙げてアルゴリズムを理解しましょう。
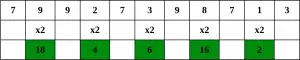
口座番号の例を考えてみましょう 79927398713 。

ステップ1 – 右端の桁から始めて、2 桁ごとに値を 2 倍にし、

ステップ2 – 数値を 2 倍すると 2 桁の数値になる場合 (例: 6 × 2 = 12)、その積の桁を加算します (例: 12: 1 + 2 = 3、15: 1 + 5 = 6)、1桁の数字を取得します。

ステップ3 – 次に、すべての桁の合計を計算します。

ステップ4 – 10 を法とする合計が 0 に等しい場合 (合計がゼロで終わる場合)、その数値は Luhn の公式に従って有効です。それ以外の場合は無効です。

合計は 70 で 10 の倍数であるため、口座番号は有効である可能性があります。

アイデアはシンプルです。端から横断していきます。 2 桁ごとに、加算する前に 2 倍にします。 2倍して得られた数値の2桁を加算します。

実装：

C++

// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(> const> string& cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum = 0, isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0;私--) {>> > int> d = cardNo[i] -> '0'> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits after> > // doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> > string cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > printf> (> 'This is a valid card'> );> > else> > printf> (> 'This is not a valid card'> );> > return> 0;> }>

ジャワ

// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.length();> > int> nSum => 0> ;> > boolean> isSecond => false> ;> > for> (> int> i = nDigits -> 1> ; i>=>> ;> > if> (isSecond ==> true> )> > d = d *> 2> ;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d /> 10> ;> > nSum += d %> 10> ;> > isSecond = !isSecond;> > }> > return> (nSum %> 10> ==> 0> );> }> > // Driver code> > static> public> void> main (String[] args)> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > System.out.println(> 'This is a valid card'> );> > else> > System.out.println(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

Python3

# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > > nDigits> => len> (cardNo)> > nSum> => 0> > isSecond> => False> > > for> i> in> range> (nDigits> -> 1> ,> -> 1> ,> -> 1> ):> > d> => ord> (cardNo[i])> -> ord> (> '0'> )> > > if> (isSecond> => => True> ):> > d> => d> *> 2> > > # We add two digits to handle> > # cases that make two digits after> > # doubling> > nSum> +> => d> /> /> 10> > nSum> +> => d> %> 10> > > isSecond> => not> isSecond> > > if> (nSum> %> 10> => => 0> ):> > return> True> > else> :> > return> False> # Driver code> if> __name__> => => '__main__'> :> > > cardNo> => '79927398713'> > > if> (checkLuhn(cardNo)):> > print> (> 'This is a valid card'> )> > else> :> > print> (> 'This is not a valid card'> )> # This code is contributed by rutvik_56>

C#

// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> > int> nDigits = cardNo.Length;> > int> nSum = 0;> > bool> isSecond => false> ;> > for> (> int> i = nDigits - 1; i>= 0;私--)>> ;> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += d / 10;> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> }> > // Driver code> > static> public> void> Main()> > {> > String cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > Console.WriteLine(> 'This is a valid card'> );> > else> > Console.WriteLine(> 'This is not a valid card'> );> > > }> }> // This Code is contributed by vt_m.>

JavaScript

> > // Javascript program to implement Luhn algorithm> > > // Returns true if given> > // card number is valid> > function> checkLuhn(cardNo)> > {> > let nDigits = cardNo.length;> > let nSum = 0;> > let isSecond => false> ;> > for> (let i = nDigits - 1; i>= 0;私--)>> > {> > let d = cardNo[i].charCodeAt() -> '0'> .charCodeAt();> > if> (isSecond ==> true> )> > d = d * 2;> > // We add two digits to handle> > // cases that make two digits> > // after doubling> > nSum += parseInt(d / 10, 10);> > nSum += d % 10;> > isSecond = !isSecond;> > }> > return> (nSum % 10 == 0);> > }> > > let cardNo => '79927398713'> ;> > if> (checkLuhn(cardNo))> > document.write(> 'This is a valid card'> );> > else> > document.write(> 'This is not a valid card'> );> > >

出力