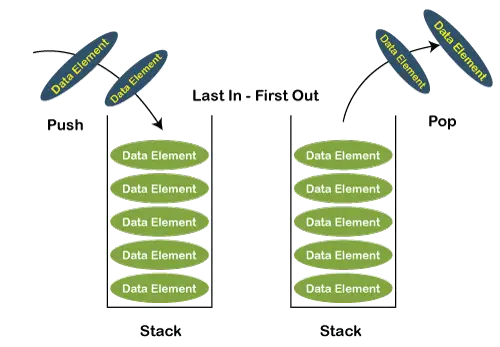
struct> Node {> > int> n;> > int> key[MAX_KEYS];> > Node* child[MAX_CHILDREN];> > bool> leaf;> };> Node* BtreeSearch(Node* x,> int> k) {> > int> i = 0;> > while> (i n && k>x->key[i]) {> > i++;> > }> > if> (i n && k == x->key[i]) {>> > return> x;> > }> > if> (x->葉){>> > return> nullptr;> > }> > return> BtreeSearch(x->child[i], k);>> C BtreeSearch(x, k)> > i = 1> > > // n[x] means number of keys in x node> > while> i ? n[x] and k ? keyi[x]> > do> i = i + 1> > if> i n[x] and k = keyi[x]> > then> return> (x, i)> > if> leaf [x]> > then> return> NIL> > else> > return> BtreeSearch(ci[x], k)> | ジャワ class> Node {> > int> n;> > int> [] key => new> int> [MAX_KEYS];> > Node[] child => new> Node[MAX_CHILDREN];> > boolean> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i => 0> ;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> | Python3 class> Node:> > def> __init__(> self> ):> > self> .n> => 0> > self> .key> => [> 0> ]> *> MAX_KEYS> > self> .child> => [> None> ]> *> MAX_CHILDREN> > self> .leaf> => True> def> BtreeSearch(x, k):> > i> => 0> > while> i and k>= x.key[i]: i += 1 if i and k == x.key[i]: return x if x.leaf: return None return BtreeSearch(x.child[i], k)>> | C# class> Node {> > public> int> n;> > public> int> [] key => new> int> [MAX_KEYS];> > public> Node[] child => new> Node[MAX_CHILDREN];> > public> bool> leaf;> }> Node BtreeSearch(Node x,> int> k) {> > int> i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> | JavaScript // Define a Node class with properties n, key, child, and leaf> class Node {> > constructor() {> > this> .n = 0;> > this> .key => new> Array(MAX_KEYS);> > this> .child => new> Array(MAX_CHILDREN);> > this> .leaf => false> ;> > }> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> > let i = 0;> > while> (i = x.key[i]) {> > i++;> > }> > if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> | 例: 入力: 指定された B ツリーで 120 を検索します。

解決:
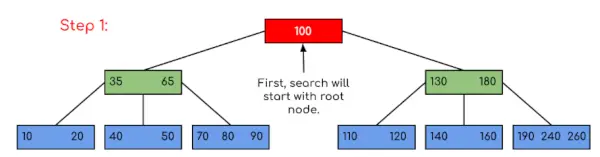
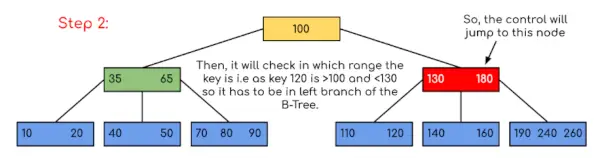
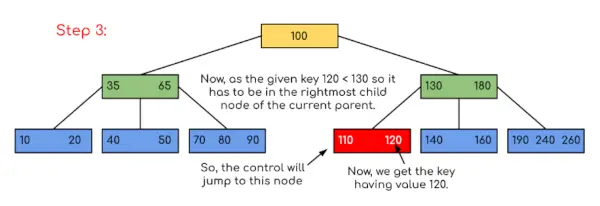 この例では、値を含むキーが存在する可能性を制限するだけで検索が短縮されたことがわかります。同様に、上記の例で 180 を探す必要がある場合、プログラムはキー 180 が現在のノード内に存在することを検出するため、制御はステップ 2 で停止します。同様に、90 を探す場合は、90 <100 となるため、自動的に左側のサブツリーに進み、制御フローは上記の例と同様になります。 上記のアプローチの実装を以下に示します。 C++ // C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> > int> * keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode** C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> public> :> > BTreeNode(> int> _t,> bool> _leaf);> // Constructor> > // A function to traverse all nodes in a subtree rooted> > // with this node> > void> traverse();> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode*> > search(> int> k);> // returns NULL if k is not present.> > // Make the BTree friend of this so that we can access> > // private members of this class in BTree functions> > friend> class> BTree;> };> // A BTree> class> BTree {> > BTreeNode* root;> // Pointer to root node> > int> t;> // Minimum degree> public> :> > // Constructor (Initializes tree as empty)> > BTree(> int> _t)> > {> > root = NULL;> > t = _t;> > }> > // function to traverse the tree> > void> traverse()> > {> > if> (root != NULL)> > root->トラバース();>>' }> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(> int> _t,> bool> _leaf)> {> > // Copy the given minimum degree and leaf property> > t = _t;> > leaf = _leaf;> > // Allocate memory for maximum number of possible keys> > // and child pointers> > keys => new> int> [2 * t - 1];> > C => new> BTreeNode*[2 * t];> > // Initialize the number of keys as 0> > n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> > // There are n keys and n+1 children, traverse through n> > // keys and first n children> > int> i;> > for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->トラバース(); コート < < ' ' < < keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->トラバース(); } // このノードをルートとするサブツリー内のキー k を検索する関数 BTreeNode* BTreeNode::search(int k) { // k 以上の最初のキーを検索 int i = 0; while (i キー[i]) i++; // 見つかったキーが k に等しい場合、このノードを返します if (keys[i] == k) return this; // ここでキーが見つからず、これがリーフ ノードの場合 if (leaf == true) NULL を返します。 // 適切な子に移動します return C[i]->search(k); }>> | ジャワ // Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > System.out.println();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > boolean> > leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> boolean> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [> 2> * t -> 1> ];> > this> .C => new> BTreeNode[> 2> * t];> > this> .n => 0> ;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i => 0> ;> > for> (i => 0> ; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > System.out.print(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i => 0> ;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }> | Python3 # Create a node> class> BTreeNode:> > def> __init__(> self> , leaf> => False> ):> > self> .leaf> => leaf> > self> .keys> => []> > self> .child> => []> # Tree> class> BTree:> > def> __init__(> self> , t):> > self> .root> => BTreeNode(> True> )> > self> .t> => t> > # Insert node> > def> insert(> self> , k):> > root> => self> .root> > if> len> (root.keys)> => => (> 2> *> self> .t)> -> 1> :> > temp> => BTreeNode()> > self> .root> => temp> > temp.child.insert(> 0> , root)> > self> .split_child(temp,> 0> )> > self> .insert_non_full(temp, k)> > else> :> > self> .insert_non_full(root, k)> > # Insert nonfull> > def> insert_non_full(> self> , x, k):> > i> => len> (x.keys)> -> 1> > if> x.leaf:> > x.keys.append((> None> ,> None> ))> > while> i>>> => 0> and> k[> 0> ] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 および k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # 子を分割します def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] y.leaf でない場合: z.child = y.child[t: 2 * t] y。 child = y.child[0: t - 1] # ツリーを出力します def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # ツリー内のキーを検索 def search_key(self, k, x=None): x が None でない場合: i = 0 while i x.keys[i][0]: i += 1 if i | C# // C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> > public> BTreeNode root;> // Pointer to root node> > public> int> t;> // Minimum degree> > // Constructor (Initializes tree as empty)> > Btree(> int> t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > // function to traverse the tree> > public> void> traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > Console.WriteLine();> > }> > // function to search a key in this tree> > public> BTreeNode search(> int> k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> }> // A BTree node> class> BTreeNode {> > int> [] keys;> // An array of keys> > int> t;> // Minimum degree (defines the range for number> > // of keys)> > BTreeNode[] C;> // An array of child pointers> > int> n;> // Current number of keys> > bool> leaf;> // Is true when node is leaf. Otherwise false> > // Constructor> > BTreeNode(> int> t,> bool> leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> int> [2 * t - 1];> > this> .C => new> BTreeNode[2 * t];> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted> > // with this node> > public> void> traverse()> > {> > // There are n keys and n+1 children, traverse> > // through n keys and first n children> > int> i = 0;> > for> (i = 0; i <> this> .n; i++) {> > // If this is not leaf, then before printing> > // key[i], traverse the subtree rooted with> > // child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > Console.Write(keys[i] +> ' '> );> > }> > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > // A function to search a key in the subtree rooted with> > // this node.> > public> BTreeNode search(> int> k)> > {> // returns NULL if k is not present.> > // Find the first key greater than or equal to k> > int> i = 0;> > while> (i keys[i])> > i++;> > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > // If the key is not found here and this is a leaf> > // node> > if> (leaf ==> true> )> > return> null> ;> > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by Rajput-Ji> | JavaScript // Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> > // Constructor (Initializes tree as empty)> > constructor(t)> > {> > this> .root => null> ;> > this> .t = t;> > }> > > // function to traverse the tree> > traverse()> > {> > if> (> this> .root !=> null> )> > this> .root.traverse();> > document.write(> ' '> );> > }> > > // function to search a key in this tree> > search(k)> > {> > if> (> this> .root ==> null> )> > return> null> ;> > else> > return> this> .root.search(k);> > }> > }> // A BTree node> class BTreeNode> {> > // Constructor> > constructor(t,leaf)> > {> > this> .t = t;> > this> .leaf = leaf;> > this> .keys => new> Array(2 * t - 1);> > this> .C => new> Array(2 * t);> > this> .n = 0;> > }> > // A function to traverse all nodes in a subtree rooted with this node> > traverse()> > {> > // There are n keys and n+1 children, traverse through n keys> > // and first n children> > let i = 0;> > for> (i = 0; i <> this> .n; i++) {> > > // If this is not leaf, then before printing key[i],> > // traverse the subtree rooted with child C[i].> > if> (> this> .leaf ==> false> ) {> > C[i].traverse();> > }> > document.write(keys[i] +> ' '> );> > }> > > // Print the subtree rooted with last child> > if> (leaf ==> false> )> > C[i].traverse();> > }> > > // A function to search a key in the subtree rooted with this node.> > search(k)> // returns NULL if k is not present.> > {> > > // Find the first key greater than or equal to k> > let i = 0;> > while> (i keys[i])> > i++;> > > // If the found key is equal to k, return this node> > if> (keys[i] == k)> > return> this> ;> > > // If the key is not found here and this is a leaf node> > if> (leaf ==> true> )> > return> null> ;> > > // Go to the appropriate child> > return> C[i].search(k);> > }> }> // This code is contributed by patel2127> |
注記: 上記のコードにはドライバー プログラムが含まれていません。プログラム全体については次回の投稿で説明する予定です。 B ツリーの挿入 。 B ツリーを定義するには 2 つの規則があります。1 つは最小次数で定義するもの、2 つ目は次数で定義するものです。私たちは最低学位の慣例に従っており、B-Tree の今後の投稿でも同様に従う予定です。上記のプログラムで使用されている変数名も同じです。 B ツリーのアプリケーション: - 大規模なデータベースで、ディスクに保存されているデータにアクセスするために使用されます。
- B ツリーを使用すると、データ セット内のデータの検索を大幅に短縮できます。
- インデックス作成機能を使用すると、複数レベルのインデックス作成を実現できます。
- ほとんどのサーバーも B ツリー アプローチを使用しています。
- B ツリーは、CAD システムで幾何学データを整理および検索するために使用されます。
- B ツリーは、自然言語処理、コンピューター ネットワーク、暗号化などの他の分野でも使用されます。
B ツリーの利点: - B ツリーは、挿入、削除、検索などの基本操作に対して O(log n) の時間計算量が保証されているため、大規模なデータ セットやリアルタイム アプリケーションに適しています。
- B ツリーは自己バランスをとります。
- 高い同時実行性と高いスループット。
- ストレージの効率的な利用。
B ツリーの欠点: - B ツリーはディスクベースのデータ構造に基づいているため、ディスク使用率が高くなる可能性があります。
- すべてのケースに最適というわけではありません。
- 他のデータ構造と比較して遅い。
挿入と削除:
B ツリーの挿入
B ツリーの削除
|



そして