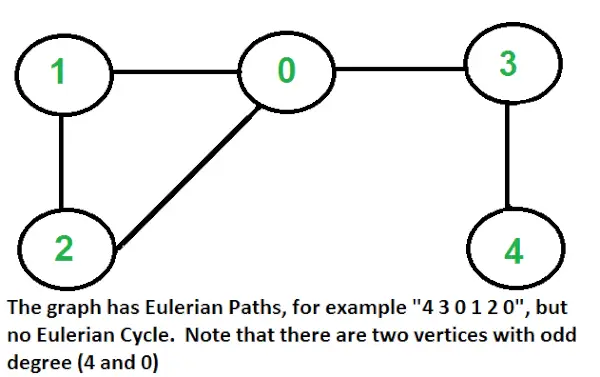
オイラーパス は、すべてのエッジを 1 回だけ訪問するグラフ内のパスです。オイラー回路は、同じ頂点で始まり同じ頂点で終わるオイラー パスです。

与えられたグラフがオイラー型かどうかを調べるにはどうすればよいでしょうか?

問題は次の質問と同じです。鉛筆を紙から離さず、エッジを複数回なぞらずに、特定のグラフを描くことは可能ですか。
グラフにオイラー サイクルがある場合はオイラーと呼ばれ、オイラー パスがある場合はセミオイラーと呼ばれます。この問題は、一般的なグラフの NP 完全問題であるハミルトニアン パスに似ているように見えます。幸いなことに、特定のグラフにオイラー パスがあるかどうかを多項式時間で見つけることができます。実際、O(V+E) 時間でそれを見つけることができます。
以下は、オイラー パスとサイクルを備えた無向グラフの興味深い特性の一部です。これらのプロパティを使用して、グラフがオイラー型かどうかを確認できます。

オイラーサイクル: 次の 2 つの条件が真の場合、無向グラフはオイラー サイクルを持ちます。

1. ゼロ以外の次数を持つすべての頂点が接続されます。ゼロ度の頂点はオイラー サイクルまたはパスに属していないため、気にしません (すべてのエッジのみを考慮します)。
2. すべての頂点の次数は均等です。

オイラーパス: 次の 2 つの条件が真の場合、無向グラフにはオイラー パスがあります。

1. オイラーサイクルの条件(a)と同じ。
2. 0 または 2 つの頂点の次数が奇数で、他のすべての頂点の次数が偶数の場合。無向グラフでは、奇数の次数を持つ頂点が 1 つだけ存在することはできないことに注意してください (無向グラフでは、すべての次数の合計は常に偶数になります)。

エッジのないグラフは、横断するエッジがないため、オイラーグラフであるとみなされることに注意してください。

これはどのように作動しますか？
オイラー パスでは、頂点 v を訪問するたびに、v を 1 つの終点として 2 つの未訪問のエッジを通過します。したがって、オイラー パスのすべての中間頂点は偶数次数を持つ必要があります。オイラー サイクルの場合、どの頂点も中間頂点になる可能性があるため、すべての頂点の次数が偶数である必要があります。

おすすめの練習用オイラー回路とパス 試してみよう！

実装：

C++

// A C++ program to check if a given graph is Eulerian or not> #include> #include> using> namespace> std;> // A class that represents an undirected graph> class> Graph> {> > int> V;> // No. of vertices> > list <> int> >*形容詞;>> // A dynamic array of adjacency lists> public> :> > // Constructor and destructor> > Graph(> int> V) {> this> ->V = V; adj =>> new> list <> int> >[で]; }>> > ~Graph() {> delete> [] adj; }> // To avoid memory leak> > // function to add an edge to graph> > void> addEdge(> int> v,> int> w);> > // Method to check if this graph is Eulerian or not> > int> isEulerian();> > // Method to check if all non-zero degree vertices are connected> > bool> isConnected();> > // Function to do DFS starting from v. Used in isConnected();> > void> DFSUtil(> int> v,> bool> visited[]);> };> void> Graph::addEdge(> int> v,> int> w)> {> > adj[v].push_back(w);> > adj[w].push_back(v);> // Note: the graph is undirected> }> void> Graph::DFSUtil(> int> v,> bool> visited[])> {> > // Mark the current node as visited and print it> > visited[v] => true> ;> > // Recur for all the vertices adjacent to this vertex> > list <> int> >::反復子 i;>>'

ジャワ

// A Java program to check if a given graph is Eulerian or not> import> java.io.*;> import> java.util.*;> import> java.util.LinkedList;> // This class represents an undirected graph using adjacency list> // representation> class> Graph> {> > private> int> V;> // No. of vertices> > // Array of lists for Adjacency List Representation> > private> LinkedList adj[];> > // Constructor> > Graph(> int> v)> > {> > V = v;> > adj => new> LinkedList[v];> > for> (> int> i=> 0> ; i adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge(int v, int w) { adj[v].add(w);// Add w to v's list. adj[w].add(v); //The graph is undirected } // A function used by DFS void DFSUtil(int v,boolean visited[]) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex Iterator i = adj[v].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from boolean isConnected() { // Mark all the vertices as not visited boolean visited[] = new boolean[V]; int i; for (i = 0; i visited[i] = false; // Find a vertex with non-zero degree for (i = 0; i if (adj[i].size() != 0) break; // If there are no edges in the graph, return true if (i == V) return true; // Start DFS traversal from a vertex with non-zero degree DFSUtil(i, visited); // Check if all non-zero degree vertices are visited for (i = 0; i if (visited[i] == false && adj[i].size()>0) false を返します。 true を返します。 } /* 関数は次のいずれかの値を返します 0 --> グラフがオイラーでない場合 1 --> グラフにオイラー経路 (セミオイラー) がある場合 2 --> グラフにオイラー回路 (オイラー) がある場合 */ int isEulerian() { // ゼロ度以外のすべての頂点が接続されているかどうかをチェック if (isConnected() == false) return 0; // 次数が奇数の頂点を数える int od = 0; for (int i = 0; i if (adj[i].size()%2!=0) od++; // count が 2 より大きい場合、グラフはオイラー関数ではありません if (odd> 2) return 0; / / 奇数カウントが 2 の場合、半オイラー関数。 // 奇数カウントが 0 の場合、オイラー関数。 // 無向グラフの戻り値では奇数カウントは 1 にならないことに注意してください (odd==2) } //テストケースを実行する関数 void test() { int res = isEulerian(); if (res == 0) System.out.println('graph is not Eulerian'); else if (res == 1) System. out.println('グラフにはオイラー パスがあります'); else System.out.println('グラフにはオイラー サイクルがあります'); // ドライバー メソッド public static void main(String args[]); / 上の図に示すグラフを作成してテストしてみましょう。 Graph g1 = new Graph(1, 0); g1.addEdge(2, 1); (0, 3); g1.addEdge(3, 4); g2.addEdge(0, 2); addEdge(2, 1); g2.addEdge(4, 0); .addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // 3 つの頂点をサイクルの形で接続したグラフを作成しましょう。 // Graph g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // すべての頂点を含むグラフを作成しましょう。 // 0 度のグラフ g5 = new Graph(3); g5.test(); } } // このコードは Aakash Hasija によって提供されています>>

Python3

# Python program to check if a given graph is Eulerian or not> #Complexity : O(V+E)> from> collections> import> defaultdict> # This class represents a undirected graph using adjacency list representation> class> Graph:> > def> __init__(> self> , vertices):> > self> .V> => vertices> # No. of vertices> > self> .graph> => defaultdict(> list> )> # default dictionary to store graph> > # function to add an edge to graph> > def> addEdge(> self> , u, v):> > self> .graph[u].append(v)> > self> .graph[v].append(u)> > # A function used by isConnected> > def> DFSUtil(> self> , v, visited):> > # Mark the current node as visited> > visited[v]> => True> > # Recur for all the vertices adjacent to this vertex> > for> i> in> self> .graph[v]:> > if> visited[i]> => => False> :> > self> .DFSUtil(i, visited)> > '''Method to check if all non-zero degree vertices are> > connected. It mainly does DFS traversal starting from> > node with non-zero degree'''> > def> isConnected(> self> ):> > # Mark all the vertices as not visited> > visited> => [> False> ]> *> (> self> .V)> > # Find a vertex with non-zero degree> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i]) !> => 0> :> > break> > # If there are no edges in the graph, return true> > if> i> => => self> .V> -> 1> :> > return> True> > # Start DFS traversal from a vertex with non-zero degree> > self> .DFSUtil(i, visited)> > # Check if all non-zero degree vertices are visited> > for> i> in> range> (> self> .V):> > if> visited[i]> => => False> and> len> (> self> .graph[i])>>> 0> :> > return> False> > return> True> > '''The function returns one of the following values> > 0 -->グラフがオイラー関数でない場合> > 1 -->グラフにオイラー経路(セミオイラー経路)がある場合> > 2 -->グラフにオイラー回路 (オイラー) がある場合 '''> > def> isEulerian(> self> ):> > # Check if all non-zero degree vertices are connected> > if> self> .isConnected()> => => False> :> > return> 0> > else> :> > # Count vertices with odd degree> > odd> => 0> > for> i> in> range> (> self> .V):> > if> len> (> self> .graph[i])> %> 2> !> => 0> :> > odd> +> => 1> > '''If odd count is 2, then semi-eulerian.> > If odd count is 0, then eulerian> > If count is more than 2, then graph is not Eulerian> > Note that odd count can never be 1 for undirected graph'''> > if> odd> => => 0> :> > return> 2> > elif> odd> => => 2> :> > return> 1> > elif> odd>>> 2> :> > return> 0> > # Function to run test cases> > def> test(> self> ):> > res> => self> .isEulerian()> > if> res> => => 0> :> > print> (> 'graph is not Eulerian'> )> > elif> res> => => 1> :> > print> (> 'graph has a Euler path'> )> > else> :> > print> (> 'graph has a Euler cycle'> )> # Let us create and test graphs shown in above figures> g1> => Graph(> 5> )> g1.addEdge(> 1> ,> 0> )> g1.addEdge(> 0> ,> 2> )> g1.addEdge(> 2> ,> 1> )> g1.addEdge(> 0> ,> 3> )> g1.addEdge(> 3> ,> 4> )> g1.test()> g2> => Graph(> 5> )> g2.addEdge(> 1> ,> 0> )> g2.addEdge(> 0> ,> 2> )> g2.addEdge(> 2> ,> 1> )> g2.addEdge(> 0> ,> 3> )> g2.addEdge(> 3> ,> 4> )> g2.addEdge(> 4> ,> 0> )> g2.test()> g3> => Graph(> 5> )> g3.addEdge(> 1> ,> 0> )> g3.addEdge(> 0> ,> 2> )> g3.addEdge(> 2> ,> 1> )> g3.addEdge(> 0> ,> 3> )> g3.addEdge(> 3> ,> 4> )> g3.addEdge(> 1> ,> 3> )> g3.test()> # Let us create a graph with 3 vertices> # connected in the form of cycle> g4> => Graph(> 3> )> g4.addEdge(> 0> ,> 1> )> g4.addEdge(> 1> ,> 2> )> g4.addEdge(> 2> ,> 0> )> g4.test()> # Let us create a graph with all vertices> # with zero degree> g5> => Graph(> 3> )> g5.test()> # This code is contributed by Neelam Yadav>

C#

// A C# program to check if a given graph is Eulerian or not> using> System;> using> System.Collections.Generic;> > // This class represents an undirected graph using adjacency list> // representation> public> class> Graph> {> > private> int> V;> // No. of vertices> > > // Array of lists for Adjacency List Representation> > private> List <> int> >[]adj;>>' >

JavaScript

> // A Javascript program to check if a given graph is Eulerian or not> // This class represents an undirected graph using adjacency list> // representation> class Graph> {> > // Constructor> > constructor(v)> > {> > this> .V = v;> > this> .adj => new> Array(v);> > for> (let i = 0; i this.adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this.adj[v].push(w);// Add w to v's list. this.adj[w].push(v); //The graph is undirected } // A function used by DFS DFSUtil(v,visited) { // Mark the current node as visited visited[v] = true; // Recur for all the vertices adjacent to this vertex for(let i of this.adj[v]) { let n = i; if (!visited[n]) this.DFSUtil(n, visited); } } // Method to check if all non-zero degree vertices are // connected. It mainly does DFS traversal starting from isConnected() { // Mark all the vertices as not visited let visited = new Array(this.V); let i; for (i = 0; i 0) false を返します。 true を返します。 } /* 関数は次のいずれかの値を返します 0 --> グラフがオイラーでない場合 1 --> グラフにオイラー経路 (セミオイラー) がある場合 2 --> グラフにオイラー回路 (オイラー) がある場合 */ isEulerian() { // ゼロ度以外のすべての頂点が接続されているかどうかをチェック if (this.isConnected() == false) return 0; // 奇数次数の頂点を数える let odd = 0; for (i = 0 とする; i 2) 0 を返します。 // 奇数カウントが 2 の場合、セミオイラー式。 // 奇数カウントが 0 の場合、オイラー // 無向グラフの戻り値 (odd==2) では、奇数カウントは 1 にならないことに注意してください。 1:2; } // テストケースを実行する関数 test() { let res = this.isEulerian(); if (res == 0) document.write('グラフはオイラー関数ではありません '); else if (res == 1) document.write('グラフにはオイラー パスがあります '); else document.write('グラフにはオイラーサイクルがあります '); } } // ドライバー メソッド // 上の図に示すグラフを作成してテストしましょう let g1 = new Graph(5); g1.addEdge(1, 0); g1.addEdge(0, 2); g1.addEdge(2, 1); g1.addEdge(0, 3); g1.addEdge(3, 4); g1.test(); g2 = 新しいグラフ(5) とします。 g2.addEdge(1, 0); g2.addEdge(0, 2); g2.addEdge(2, 1); g2.addEdge(0, 3); g2.addEdge(3, 4); g2.addEdge(4, 0); g2.test(); g3 = 新しいグラフ(5) とします。 g3.addEdge(1, 0); g3.addEdge(0, 2); g3.addEdge(2, 1); g3.addEdge(0, 3); g3.addEdge(3, 4); g3.addEdge(1, 3); g3.test(); // 3 つの頂点をサイクルの形で接続したグラフを作成しましょう let g4 = new Graph(3); g4.addEdge(0, 1); g4.addEdge(1, 2); g4.addEdge(2, 0); g4.test(); // すべての頂点を含むグラフを作成しましょう。 // 度 0 で let g5 = new Graph(3); g5.test(); // このコードは avanitrachhadiya2155 によって寄稿されました>>

出力

graph has a Euler path graph has a Euler cycle graph is not Eulerian graph has a Euler cycle graph has a Euler cycle 

時間計算量: O(V+E)

空間の複雑さ: O(V+E)

次の記事:
有向グラフのオイラー パスと回路。
オイラーパスまたは回路を印刷するフルーリーのアルゴリズム?