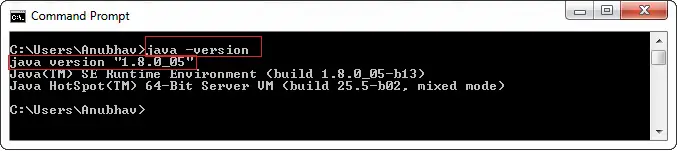
デコーダ

2進数の情報を2つに変換する組み合わせ回路 N 出力行は次のように知られています デコーダー。 バイナリ情報は N 入力行の形式で渡されます。出力行は 2 つの要素を定義します。 N -バイナリ情報のビットコード。簡単に言うと、 デコーダ の逆の操作を実行します。 エンコーダ 。簡単にするために、一度に 1 つの入力ラインだけがアクティブになります。制作した2 N -bit 出力コードはバイナリ情報に相当します。

デコーダには次のようなさまざまなタイプがあります。
2~4ラインデコーダ:
2 ~ 4 ライン デコーダには、合計 3 つの入力があります。つまり、A 0 、A 1 E と 4 つの出力、つまり Y 0 、 そして 1 、 そして 2 、Y 3 。入力の各組み合わせについて、イネーブル「E」が 1 に設定されている場合、これら 4 つの出力の 1 つが 1 になります。2 ~ 4 ライン デコーダのブロック図と真理値表を以下に示します。
ブロック図:

真理値表:

項 Y0、Y0、Y2、および Y3 の論理式は次のとおりです。
そして 3 =E.A. 1 .A 0
そして 2 =E.A. 1 .A 0 '
そして 1 =E.A. 1 '.A 0
Y0=E.A. 1 '.A 0 '
上記の式の論理回路は次のとおりです。

3~8ラインデコーダ:
3 ~ 8 ライン デコーダは、としても知られています。 2進数から8進数へのデコーダ 。 3 ~ 8 ラインのデコーダには、合計 8 つの出力があります。つまり、Y 0 、 そして 1 、 そして 2 、 そして 3 、 そして 4 、 そして 5 、 そして 6 、Y 7 および 3 つの出力、つまり A 0 、A1、およびA 2 。この回路にはイネーブル入力「E」があります。 2 ~ 4 ライン デコーダと同様に、イネーブル「E」が 1 に設定されている場合、これら 4 つの出力の 1 つが 1 になります。3 ~ 8 ライン エンコーダのブロック図と真理値表を以下に示します。
ブロック図:

真理値表:

項Yの論理式 0 、 そして 1 、 そして 2 、 そして 3 、 そして 4 、 そして 5 、 そして 6 、Y 7 以下のとおりであります:
そして 0 =A 0 '.A 1 '.A 2 '
そして 1 =A 0 .A 1 '.A 2 '
そして 2 =A 0 '.A 1 .A 2 '
そして 3 =A 0 .A 1 .A 2 '
そして 4 =A 0 '.A 1 '.A 2
そして 5 =A 0 .A 1 '.A 2
そして 6 =A 0 '.A 1 .A 2
そして 7 =A 0 .A 1 .A 2
上記の式の論理回路は次のとおりです。

4~16ラインデコーダ
4 ~ 16 ライン デコーダには、合計 16 個の出力があります。つまり、Y 0 、 そして 1 、 そして 2 、……、 そして 16 および 4 つの入力、つまり A 0 、A1、A 2 、A 3 。 3 ~ 16 ライン デコーダは、2 ~ 4 デコーダまたは 3 ~ 8 デコーダのいずれかを使用して構築できます。必要な下位デコーダの数を求めるには次の式があります。
必要な下位デコーダの数=m 2 /分 1
メートル 1 = 8
メートル 2 = 16
必要なデコーダ数は 3 ~ 8 個 =  =2
=2
ブロック図:

真理値表:

項 A0、A1、A2、…、A15 の論理式は次のとおりです。
そして 0 =A 0 '.A 1 '.A 2 '.A 3 '
そして 1 =A 0 '.A 1 '.A 2 '.A 3
そして 2 =A 0 '.A 1 '.A 2 .A 3 '
そして 3 =A 0 '.A 1 '.A 2 .A 3
そして 4 =A 0 '.A 1 .A 2 '.A 3 '
そして 5 =A 0 '.A 1 .A 2 '.A 3
そして 6 =A 0 '.A 1 .A 2 .A 3 '
そして 7 =A 0 '.A 1 .A 2 .A 3
そして 8 =A 0 .A 1 '.A 2 '.A 3 '
そして 9 =A 0 .A 1 '.A 2 '.A 3
そして 10 =A 0 .A 1 '.A 2 .A 3 '
そして 十一 =A 0 .A 1 '.A 2 .A 3
そして 12 =A 0 .A 1 .A 2 '.A 3 '
そして 13 =A 0 .A 1 .A 2 '.A 3
そして 14 =A 0 .A 1 .A 2 .A 3 '
そして 15 =A 0 .A 1 .A 2 '.A 3
上記の式の論理回路は次のとおりです。