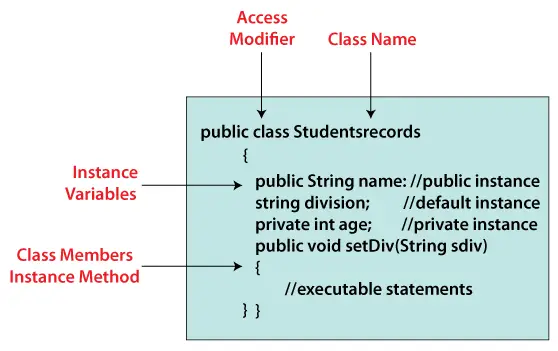
アルゴリズムの分析 | BIG - Θ (ビッグシータ) 表記法 - TECHCODEVIEW.COM

の中にアルゴリズムの分析、漸近表記は、アルゴリズムのパフォーマンスを評価するために使用されます。最良のケースと最悪のケース。この記事では、ギリシャ文字 (Θ) で表される Big – Theta 記法について説明します。

意味： g と f を自然数の集合からそれ自体への関数とする。定数 c がある場合、関数 f は Θ(g) であると言われます。 ₁ 、c ₂ > 0 および自然数 n ₀ そのようなc ₁ * g(n) ≤ f(n) ≤ c ₂ * すべての n ≥ n に対する g(n) ₀

数学的表現:

Θ (g(n)) = {f(n): 正の定数 c が存在します。 ₁ 、c ₂ そしてn ₀ 0 ≤ c となるように ₁ * g(n) ≤ f(n) ≤ c ₂ * すべての n ≥ n に対する g(n) ₀ }
注: Θ(g) は集合です

上記の定義は、f(n) が g(n) のシータである場合、n の値が大きい場合 (n ≥ n)、値 f(n) は常に c1 * g(n) と c2 * g(n) の間にあることを意味します。 ₀ ）。シータの定義では、n の値が n よりも大きい場合に f(n) が負でないことも必要です。 ₀ 。

グラフ表示：

グラフ表示

簡単に言うと、Big – Theta(Θ) 表記は、関数 f(n) の漸近限界 (上限と下限の両方) を指定し、アルゴリズムの平均時間計算量を提供します。

プログラムの平均時間複雑さを調べるには、次の手順に従います。

プログラムをより小さなセグメントに分割します。
入力のすべてのタイプと数を検索し、実行に必要な操作の数を計算します。入力ケースが均等に分散されていることを確認してください。
すべての計算値の合計を求め、その合計を入力の総数で割ります。すべての定数を削除した後の得られた n の関数が g(n) であるとします。Θ 表記では Θ(g(n)) と表されます。

例：次の例を考えてみましょう線形検索を使用して、キーが配列内に存在するかどうかを確認します。。アイデアは次のとおりです配列を走査するすべての要素がキーと等しいかどうかを確認します。

疑似コードは次のとおりです。

bool linearSearch(int a[], int n, int key) {  for (int i = 0; i   if (a[i] == key)  return true;  }   return false; }

上記のアプローチの実装を以下に示します。

C++

// C++ program for the above approach> #include> using> namespace> std;> // Function to find whether a key exists in an> // array or not using linear search> bool> linearSearch(> int> a[],> int> n,> int> key)> {> > // Traverse the given array, a[]> > for> (> int>

i = 0; i   // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver Code int main() {  // Given Input  int arr[] = { 2, 3, 4, 10, 40 };  int x = 10;  int n = sizeof(arr) / sizeof(arr[0]);  // Function Call    if (linearSearch(arr, n, x))  cout  < < 'Element is present in array';  else  cout  < < 'Element is not present in array';  return 0; }>

ジャワ

// Java program for the above approach> import> java.lang.*;> import> java.util.*;> class> GFG{> // Function to find whether a key exists in an> // array or not using linear search> static> boolean> linearSearch(> int> a[],> int> n,> > int> key)> {> > > // Traverse the given array, a[]> > for> (> int> i => 0>

; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver code public static void main(String[] args) {    // Given Input  int arr[] = { 2, 3, 4, 10, 40 };  int x = 10;  int n = arr.length;  // Function Call  if (linearSearch(arr, n, x))  System.out.println('Element is present in array');  else  System.out.println('Element is not present in array'); } } // This code is contributed by avijitmondal1998>

Python3

# Python3 program for the above approach> # Function to find whether a key exists in an> # array or not using linear search> def> linearSearch(a, n, key):> > # Traverse the given array, a[]> > for> i> in> range> (> 0> , n):> > # Check if a[i] is equal to key> > if> (a[i]> => => key):> > return> True> > > return> False> # Driver Code> # Given Input> arr> => 2> ,> 3> ,> 4> ,> 10> ,> 40> x> => 10> n> => len> (arr)> # Function Call> if> (linearSearch(arr, n, x)):> > print> (> 'Element is present in array'> )> else> :> > print> (> 'Element is not present in array'> )> > # This code is contributed by shivanisinghss2110>

C#

// C# program for above approach> using> System;> class> GFG{> // Function to find whether a key exists in an> // array or not using linear search> static> bool> linearSearch(> int> [] a,> int> n,> > int> key)> {> > > // Traverse the given array, a[]> > for> (> int>

i = 0; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver Code static void Main() {  // Given Input  int[] arr = { 2, 3, 4, 10, 40 };  int x = 10;  int n = arr.Length;  // Function Call  if (linearSearch(arr, n, x))  Console.Write('Element is present in array');  else  Console.Write('Element is not present in array'); } } // This code is contributed by sanjoy_62.>

JavaScript

> // JavaScript program for the above approach> // Function to find whether a key exists in an> // array or not using linear search> function> linearSearch(a, n, key)> {> > > // Traverse the given array, a[]> > for> (> var>

i = 0; i   {    // Check if a[i] is equal to key  if (a[i] == key)  return true;  }  return false; } // Driver code  // Given Input  var arr = [ 2, 3, 4, 10, 40 ];  var x = 10;  var n = arr.length;  // Function Call  if (linearSearch(arr, n, x))  document.write('Element is present in array');  else  document.write('Element is not present in array'); // This code is contributed by shivanisinghss2110>

出力

Element is present in array

時間計算量: の上）
補助スペース: ○(1)

線形探索問題では、すべてのケースが次のようになると仮定しましょう。均一に分布 (キーが配列に存在しない場合を含みます)。したがって、すべての場合 (キーが位置 1、2、3、……、n に存在する場合と存在しない場合) を合計し、その合計を n + 1 で割ります。

平均ケース時間の複雑さ = $frac{sum_{i=1}^{n+1} heta(i)}{n + 1}$

⇒ $frac{ heta((n+1)*(n+2)/2)}{n+1}$

⇒

⇒ (定数は削除されます)

Big – Θ 表記を使用する場合: Big – Θ は、Big – Θ の計算中にさまざまなタイプと長さの入力の一様分布が考慮されるため、最も正確な精度でアルゴリズムを分析します。これにより、分析中に最も正確なアルゴリズムの平均時間計算量が得られますが、実際には場合によっては、アルゴリズムに均一に分散された入力セットを見つけることが困難になることがあります。その場合は、ビッグオー表記関数 f の漸近上限を表すが使用されます。

詳細については、以下を参照してください。アルゴリズムの設計と解析。