מפענח

המעגל השילובי שמשנה את המידע הבינארי ל-2 נ קווי פלט ידועים בשם מפענחים. המידע הבינארי מועבר בצורה של N שורות קלט. קווי הפלט מגדירים את ה-2 נ -קוד סיביות עבור המידע הבינארי. במילים פשוטות, ה מפענח מבצע את הפעולה ההפוכה של קוֹדַאִי . בכל פעם, רק קו קלט אחד מופעל למען הפשטות. ה-2 שהופק נ קוד פלט -bit שווה ערך למידע הבינארי.

ישנם סוגים שונים של מפענחים שהם כדלקמן:
מפענח 2 עד 4 שורות:
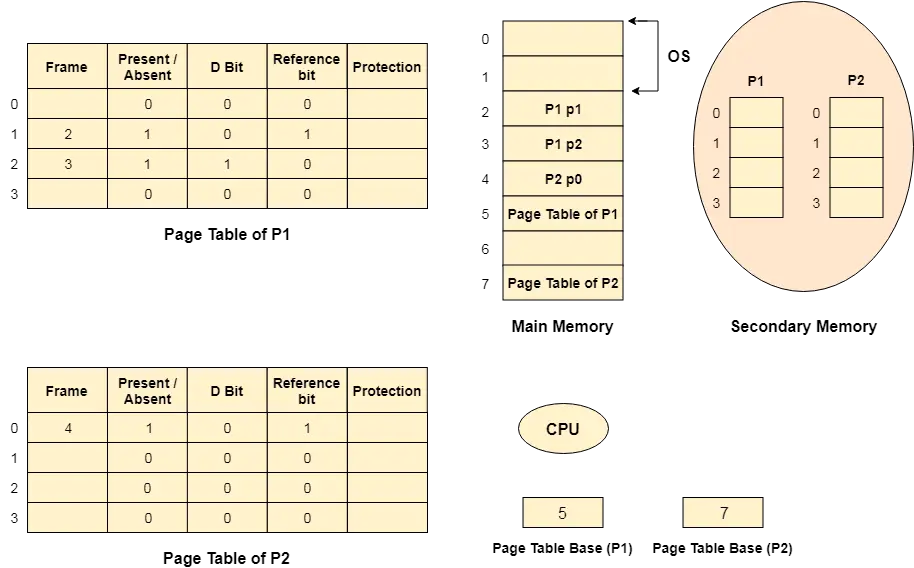
במפענח 2 עד 4 קווים, יש בסך הכל שלוש כניסות, כלומר, A 0 , ו-A 1 ו-E וארבעה יציאות, כלומר Y 0 , ו 1 , ו 2 , ו-Y 3 . עבור כל שילוב של כניסות, כאשר ה-Enable 'E' מוגדר ל-1, אחת מארבע היציאות הללו תהיה 1. דיאגרמת הבלוק וטבלת האמת של מפענח 2 עד 4 קווים ניתנות להלן.
תרשים בלוקים:

שולחן האמת:

הביטוי הלוגי של המונח Y0, Y0, Y2 ו-Y3 הוא כדלקמן:
ו 3 =E.A 1 .א 0
ו 2 =E.A 1 .א 0 '
ו 1 =E.A 1 '.א 0
Y0=E.A 1 '.א 0 '
מעגל לוגי של הביטויים לעיל ניתן להלן:

מפענח 3 עד 8 שורות:
מפענח 3 עד 8 שורות ידוע גם בשם מפענח בינארי לאוקטלי . במפענח בן 3 עד 8 קווים, יש בסך הכל שמונה יציאות, כלומר Y 0 , ו 1 , ו 2 , ו 3 , ו 4 , ו 5 , ו 6 , ו-Y 7 ושלוש יציאות, כלומר, A 0 , A1 ו-A 2 . למעגל זה יש כניסת הפעלה 'E'. בדיוק כמו מפענח של 2 עד 4 קווים, כאשר ההפעלה 'E' מוגדרת ל-1, אחת מארבעת היציאות הללו תהיה 1. דיאגרמת הבלוק וטבלת האמת של מקודד 3 עד 8 קווים ניתנות להלן.
תרשים בלוקים:

שולחן האמת:

הביטוי ההגיוני של המונח Y 0 , ו 1 , ו 2 , ו 3 , ו 4 , ו 5 , ו 6 , ו-Y 7 הוא כדלקמן:
ו 0 =א 0 '.א 1 '.א 2 '
ו 1 =א 0 .א 1 '.א 2 '
ו 2 =א 0 '.א 1 .א 2 '
ו 3 =א 0 .א 1 .א 2 '
ו 4 =א 0 '.א 1 '.א 2
ו 5 =א 0 .א 1 '.א 2
ו 6 =א 0 '.א 1 .א 2
ו 7 =א 0 .א 1 .א 2
מעגל לוגי של הביטויים לעיל ניתן להלן:

מפענח 4 עד 16 שורות
במפענח 4 עד 16 קווים, יש בסך הכל 16 יציאות, כלומר Y 0 , ו 1 , ו 2 ,……, ו 16 וארבעה כניסות, כלומר, A 0 , A1, A 2 , ו-A 3 . ניתן לבנות את המפענח בן 3 עד 16 שורות באמצעות מפענח של 2 עד 4 או מפענח של 3 עד 8. יש את הנוסחה הבאה המשמשת כדי למצוא את המספר הנדרש של מפענחים מסדר נמוך יותר.
מספר נדרש של מפענחים מסדר נמוך=m 2 /M 1
M 1 = 8
M 2 = 16
מספר נדרש של 3 עד 8 מפענחים=  =2
=2
תרשים בלוקים:

שולחן האמת:

הביטוי הלוגי של המונח A0, A1, A2,..., A15 הוא כדלקמן:
ו 0 =א 0 '.א 1 '.א 2 '.א 3 '
ו 1 =א 0 '.א 1 '.א 2 '.א 3
ו 2 =א 0 '.א 1 '.א 2 .א 3 '
ו 3 =א 0 '.א 1 '.א 2 .א 3
ו 4 =א 0 '.א 1 .א 2 '.א 3 '
ו 5 =א 0 '.א 1 .א 2 '.א 3
ו 6 =א 0 '.א 1 .א 2 .א 3 '
ו 7 =א 0 '.א 1 .א 2 .א 3
ו 8 =א 0 .א 1 '.א 2 '.א 3 '
ו 9 =א 0 .א 1 '.א 2 '.א 3
ו 10 =א 0 .א 1 '.א 2 .א 3 '
ו אחד עשר =א 0 .א 1 '.א 2 .א 3
ו 12 =א 0 .א 1 .א 2 '.א 3 '
ו 13 =א 0 .א 1 .א 2 '.א 3
ו 14 =א 0 .א 1 .א 2 .א 3 '
ו חֲמֵשׁ עֶשׂרֵה =א 0 .א 1 .א 2 '.א 3
מעגל לוגי של הביטויים לעיל ניתן להלן: