Ordinamento topologico

Ordinamento topologico per Grafico aciclico diretto (DAG) è un ordinamento lineare dei vertici tale che per ogni bordo diretto u-v, vertice In viene prima In nell'ordinazione.
Nota: L'ordinamento topologico per un grafico non è possibile se il grafico non è a GIORNO .
Esempio:
Pratica consigliata Soluzione basata su DFS per trovare un ordinamento topologico è già stato discusso.Ingresso: Grafico:

Esempio
Produzione: 5 4 2 3 1 0
Spiegazione: Il primo vertice nell'ordinamento topologico è sempre un vertice con grado interno pari a 0 (un vertice senza spigoli entranti). Un ordinamento topologico del grafico seguente è 5 4 2 3 1 0. Può esserci più di un ordinamento topologico per un grafico. Un altro ordinamento topologico del grafico seguente è 4 5 2 3 1 0.
L'ordine topologico potrebbe non essere unico:
Ordinamento topologico è un problema di dipendenza in cui il completamento di un'attività dipende dal completamento di numerose altre attività il cui ordine può variare. Cerchiamo di comprendere questo concetto tramite un esempio:
Supponiamo che il nostro compito sia raggiungere la nostra Scuola e per arrivarci dobbiamo prima vestirci. La dipendenza dall'indossare vestiti è mostrata nel grafico delle dipendenze sottostante. Ad esempio non puoi indossare le scarpe prima di indossare i calzini.

Dall'immagine sopra avresti già capito che esistono diversi modi per vestirsi, l'immagine sotto mostra alcuni di questi modi.

Puoi elencare tutto il possibile ordinamento topologico di vestirsi per il grafico delle dipendenze di cui sopra?
Algoritmo per l'ordinamento topologico utilizzando DFS:
Ecco un algoritmo passo passo per l'ordinamento topologico utilizzando Depth First Search (DFS):
- Crea un grafico con N vertici e M -bordi diretti.
- Inizializza uno stack e un array visitato di dimensioni N .
- Per ogni vertice non visitato nel grafico, procedere come segue:
- Chiama la funzione DFS con il vertice come parametro.
- Nella funzione DFS, contrassegnare il vertice come visitato e chiamare ricorsivamente la funzione DFS per tutti i vicini non visitati del vertice.
- Una volta che tutti i vicini sono stati visitati, metti il vertice nella pila.
- Dopo tutto, i vertici sono stati visitati, estrai gli elementi dallo stack e li aggiungi all'elenco di output finché lo stack non è vuoto.
- L'elenco risultante è l'ordine topologicamente ordinato del grafico.
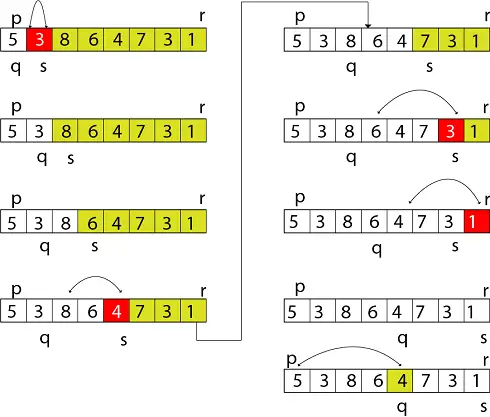
Illustrazione Algoritmo di ordinamento topologico:
L'immagine sotto è un'illustrazione dell'approccio di cui sopra:

Flusso di lavoro generale dell'ordinamento topologico
Passo 1:
- Iniziamo DFS dal nodo 0 perché ha zero nodi in entrata
- Spingiamo il nodo 0 nello stack e passiamo al nodo successivo che ha un numero minimo di nodi adiacenti, ovvero il nodo 1.

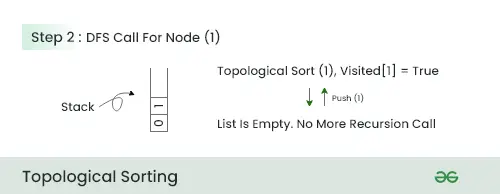
Passo 2:
- In questo passaggio, poiché non ci sono adiacenti a questo nodo, spingi il nodo 1 nello stack e passa al nodo successivo.
Passaggio 3:
- In questo passaggio, scegliamo il nodo 2 perché ha un numero minimo di nodi adiacenti dopo 0 e 1.
- Chiamiamo DFS per il nodo 2 e spingiamo tutti i nodi che attraversano il nodo 2 in ordine inverso.
- Quindi premi 3 e poi premi 2 .

Passaggio 4:
- Ora chiamiamo DFS per il nodo 4
- Perché 0 e 1 sono già presenti nello stack, quindi inseriamo semplicemente il nodo 4 nello stack e torniamo.

Passaggio 5:
- In questo passaggio, poiché tutti i nodi adiacenti di 5 sono già nello stack, inseriamo il nodo 5 nello stack e torniamo.

Passaggio 6: Questo è il passaggio finale dell'ordinamento topologico in cui estraiamo tutti gli elementi dallo stack e li stampiamo in quest'ordine.
Di seguito è riportata l’implementazione dell’approccio di cui sopra:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector >& agg, vettore & visitato, impilare & Stack) { // Contrassegna il nodo corrente come visitato visitato[v] = true; // Ricorre per tutti i vertici adiacenti for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj,visited, Stack); } // Spinge il vertice corrente nello stack che memorizza il risultato Stack.push(v); } // Funzione per eseguire l'ordinamento topologico void topologicalSort(vettore >& adj, int V) { pila Pila; // Impila per memorizzare il vettore dei risultati visitato(V, falso); // Chiama la funzione di supporto ricorsiva per memorizzare // Ordinamento topologico partendo da tutti i vertici uno per // uno per (int i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout < < Stack.top() < < ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector > bordi = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Grafico rappresentato come un vettore di lista di adiacenza > agg(V); for (auto i: bordi) { adj[i[0]].push_back(i[1]); } cout < < 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }
Giava import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List > adj, booleano[] visitato, Stack stack) { // Contrassegna il nodo corrente come visitatovisited[v] = true; // Ricorre per tutti i vertici adiacenti for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj,visited, stack); } // Spinge il vertice corrente nello stack che memorizza il // risultato stack.push(v); } // Funzione per eseguire l'ordinamento topologico static void topologicalSort(List > adj, int V) { // Stack per memorizzare lo Stack dei risultati pila = nuova pila(); booleano[] visitato = nuovo booleano[V]; // Chiama la funzione di supporto ricorsiva per memorizzare // Ordinamento topologico partendo da tutti i vertici uno // uno per uno for (int i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List > bordi = new ArrayList(); bordi.add(Arrays.asList(0, 1)); bordi.add(Arrays.asList(1, 2)); bordi.add(Arrays.asList(3, 1)); bordi.add(Arrays.asList(3, 2)); // Grafico rappresentato come elenco di adiacenze Elenco > adj = nuovo ArrayList(V); for (int i = 0; i < V; i++) { adj.add(new ArrayList()); } for (List i : bordi) { adj.get(i.get(0)).add(i.get(1)); } ordinamento topologico(agg, V); } }
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V) C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List > adj, bool[] visitato, Stack stack) { // Contrassegna il nodo corrente come visitatovisited[v] = true; // Ricorre per tutti i vertici adiacenti foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj,visited, stack); } // Spinge il vertice corrente nello stack che memorizza il // risultato stack.Push(v); } // Funzione per eseguire l'ordinamento topologico static void TopologicalSort(List > adj, int V) { // Stack per memorizzare lo Stack dei risultati pila = nuova pila (); bool[] visitato = new bool[V]; // Chiama la funzione di supporto ricorsiva per memorizzare // Ordinamento topologico partendo da tutti i vertici uno // uno per uno for (int i = 0; i < V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Codice driver static void Main(string[] args) { // Numero di nodi int V = 4; // Elenco dei bordi > bordi = nuova lista >{ nuova lista { 0, 1 }, nuova lista { 1, 2 }, nuova lista { 3, 1 }, nuova lista { 3, 2 } }; // Grafico rappresentato come elenco di adiacenze Elenco > agg = nuova Lista >(); for (int i = 0; i < V; i++) { adj.Add(new List ()); } foreach(Lista i negli archi) { adj[i[0]].Add(i[1]); } Ordinamento Topologico(agg, V); } }
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Codice driver (() => { // Numero di nodi const V = 4; // Bordi const bordi = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Grafico rappresentato come una lista di adiacenze const adj = Array.from({ length: V }, () => []); for (let i di archi) { adj[i[0]].push (i[1]); } ordinamento topologico(agg, V })(); Produzione
Topological sorting of the graph: 3 0 1 2
Complessità temporale: O(V+E). L'algoritmo sopra è semplicemente DFS con uno stack aggiuntivo. Quindi la complessità temporale è la stessa di DFS
Spazio ausiliario: O(V). Lo spazio extra è necessario per lo stack
Ordinamento topologico utilizzando BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * agg; // Puntatore a un array contenente // elenchi di adiacenza public: Graph(int V); // Costruttore void addEdge(int v, int w); // Funzione per aggiungere un bordo al grafico void topologicalSort(); // stampa un ordinamento topologico // del grafico completo }; Grafico::Grafico(int V) { questo->V = V; agg = nuova lista [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Aggiunge w all'elenco di v. } // Funzione per eseguire l'ordinamento topologico void Graph::topologicalSort() { // Crea un vettore per memorizzare il vettore in gradi di tutti i vertici in_grado(V, 0); // Attraversa gli elenchi di adiacenza per riempire in_degree di // vertici per (int v = 0; v < V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue Q; for (int i = 0; i < V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector ordine_superiore; // Rimuovi dalla coda i vertici uno per uno dalla coda e accoda // i vertici adiacenti se in grado di adiacente diventa 0 while (!q.empty()) { // Estrai la parte anteriore della coda (o esegui la rimozione dalla coda) // e aggiungilo a ordine topologico int u = q.front(); q.pop(); top_order.push_back(u); // Itera attraverso tutti i nodi vicini // del nodo deaccodato u e diminuisce il loro grado // di 1 elenco ::iteratore itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Se in-degree diventa zero, aggiungilo alla coda if (--in_degree[*itr ] == 0) q.push(*itr); conta++; } // Controlla se c'è stato un ciclo if (count != V) { cout < < 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout < < i < < ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout < < 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; } Giava import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] agg; // Elenco di adiacenze // rappresentazione del // grafico // Costruttore Graph(int V) { this.V = V; adj = nuovo ArrayList[V]; for (int i = 0; i < V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = nuova ListaCollegata(); for (int i = 0; i < V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Toglie dalla coda i vertici uno per uno dalla coda e // accoda i vertici adiacenti se nel grado di // adiacente diventa 0 while (!q.isEmpty()) { // Estrai la parte anteriore della coda e la aggiungi all' // ordine topologico int u = q.poll(); topOrder.add(u); conta++; // Itera attraverso tutti i nodi vicini del // nodo dequeued u e diminuisce il loro grado // di 1 for (int w : adj[u]) { // Se il grado diventa zero, lo aggiunge alla // coda if (--inGrado[w] == 0) q.add(w); } } // Controlla se c'era un ciclo if (count != V) { System.out.println('Il grafico contiene ciclo'); ritorno; } // Stampa l'ordine topologico per (int i : topOrder) System.out.print(i + ' '); } } // Codice driver public class Main { public static void main(String[] args) { // Crea un grafico indicato nel diagramma precedente Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Segue un ordinamento topologico del grafico dato'); g.ordinamentotopologico(); } } Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort() JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh Produzione
Following is a Topological Sort of the given graph 4 5 2 0 3 1
Complessità temporale:
La complessità temporale per la costruzione del grafo è O(V + E), dove V è il numero di vertici ed E è il numero di archi.
Anche la complessità temporale per eseguire l'ordinamento topologico utilizzando BFS è O(V + E), dove V è il numero di vertici ed E è il numero di spigoli. Questo perché ogni vertice e ogni bordo vengono visitati una volta durante l'attraversamento del BFS.
Complessità spaziale:
La complessità dello spazio per memorizzare il grafico utilizzando una lista di adiacenza è O(V + E), dove V è il numero di vertici ed E è il numero di archi.
Spazio aggiuntivo viene utilizzato per memorizzare i vertici in gradi, che richiedono spazio O (V).
Per l'attraversamento BFS viene utilizzata una coda, che può contenere al massimo V vertici. Pertanto, la complessità dello spazio per la coda è O(V).
Nel complesso, la complessità spaziale dell'algoritmo è O(V + E) a causa della memorizzazione del grafico, dell'array in gradi e della coda.
In sintesi, la complessità temporale dell'implementazione fornita è O(V + E), e anche la complessità spaziale è O(V + E).
Nota: Qui possiamo anche usare un array invece dello stack. Se viene utilizzato l'array, stampare gli elementi in ordine inverso per ottenere l'ordinamento topologico.
Vantaggi dell'ordinamento topologico:
- Aiuta nella pianificazione di attività o eventi in base alle dipendenze.
- Rileva i cicli in un grafico diretto.
- Efficiente per risolvere problemi con vincoli di precedenza.
Svantaggi dell'ordinamento topologico:
- Applicabile solo ai grafici aciclici diretti (DAG), non adatto ai grafici ciclici.
- Potrebbe non essere unico, possono esistere più ordinamenti topologici validi.
- Inefficiente per grafici di grandi dimensioni con molti nodi e spigoli.
Applicazioni dell'ordinamento topologico:
- Pianificazione delle attività e gestione dei progetti.
- Risoluzione delle dipendenze nei sistemi di gestione dei pacchetti.
- Determinazione dell'ordine di compilazione nei sistemi di compilazione del software.
- Rilevamento dei deadlock nei sistemi operativi.
- La programmazione dei corsi nelle università.
Articoli Correlati:
- Algoritmo di Kahn per l'ordinamento topologico
- Tutti i tipi topologici di un grafo aciclico diretto