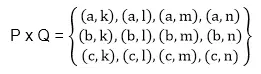Metodo stdev() nel modulo statistico Python

Il modulo Statistics in Python fornisce una funzione nota come sviluppo standard() , che può essere utilizzato per calcolare la deviazione standard. La funzione stdev() calcola solo la deviazione standard da un campione di dati, anziché da un'intera popolazione.
Per calcolare la deviazione standard di un'intera popolazione, un'altra funzione nota come pstdev() si usa.
Deviazione standard è una misura di diffusione in Statistica. Viene utilizzato per quantificare la misura della diffusione, variazione di un insieme di valori di dati. È molto simile alla varianza, fornisce la misura della deviazione mentre la varianza fornisce il valore al quadrato.
Una misura bassa della deviazione standard indica che i dati sono meno dispersi, mentre un valore elevato di deviazione standard mostra che i dati in un insieme sono dispersi rispetto ai loro valori medi medi. Una proprietà utile della deviazione standard è che, a differenza della varianza, è espressa nelle stesse unità dei dati.
Standard Deviation is calculated by : where x1, x2, x3.....xn are observed values in sample data, is the mean value of observations andN is the number of sample observations.
Sintassi: stdev( [set di dati], xbar)
Parametri:
[dati] : Un iterabile con numeri a valore reale.
xbar (Opzionale) : Prende la media effettiva del set di dati come valore.
Tipo di ritorno: Restituisce la deviazione standard effettiva dei valori passati come parametro.
Eccezioni:
Errore statistico viene generato per un set di dati con meno di 2 valori passati come parametro.
Valori impossibili/privi di precisione quando il valore fornito come xbar non corrisponde alla media effettiva del set di dati.
Codice n. 1:
Python3
# Python code to demonstrate stdev() function> # importing Statistics module> import> statistics> # creating a simple data - set> sample> => [> 1> ,> 2> ,> 3> ,> 4> ,> 5> ]> # Prints standard deviation> # xbar is set to default value of 1> print> (> 'Standard Deviation of sample is % s '> > %> (statistics.stdev(sample)))> |
Produzione :
Standard Deviation of the sample is 1.5811388300841898
Codice n.2: Dimostrare stdev() su un insieme variabile di tipi di dati
Python3
# Python code to demonstrate stdev()> # function on various range of datasets> # importing the statistics module> from> statistics> import> stdev> # importing fractions as parameter values> from> fractions> import> Fraction as fr> # creating a varying range of sample sets> # numbers are spread apart but not very much> sample1> => (> 1> ,> 2> ,> 5> ,> 4> ,> 8> ,> 9> ,> 12> )> # tuple of a set of negative integers> sample2> => (> -> 2> ,> -> 4> ,> -> 3> ,> -> 1> ,> -> 5> ,> -> 6> )> # tuple of a set of positive and negative numbers> # data-points are spread apart considerably> sample3> => (> -> 9> ,> -> 1> ,> -> 0> ,> 2> ,> 1> ,> 3> ,> 4> ,> 19> )> # tuple of a set of floating point values> sample4> => (> 1.23> ,> 1.45> ,> 2.1> ,> 2.2> ,> 1.9> )> # Print the standard deviation of> # following sample sets of observations> print> (> 'The Standard Deviation of Sample1 is % s'> > %> (stdev(sample1)))> > print> (> 'The Standard Deviation of Sample2 is % s'> > %> (stdev(sample2)))> > print> (> 'The Standard Deviation of Sample3 is % s'> > %> (stdev(sample3)))> > > print> (> 'The Standard Deviation of Sample4 is % s'> > %> (stdev(sample4)))> |
Produzione :
The Standard Deviation of Sample1 is 3.9761191895520196 The Standard Deviation of Sample2 is 1.8708286933869707 The Standard Deviation of Sample3 is 7.8182478855559445 The Standard Deviation of Sample4 is 0.41967844833872525
Codice n. 3: Dimostrare la differenza tra i risultati di variance() e stdev()
Python3
# Python code to demonstrate difference> # in results of stdev() and variance()> # importing Statistics module> import> statistics> # creating a simple data-set> sample> => [> 1> ,> 2> ,> 3> ,> 4> ,> 5> ]> # Printing standard deviation> # xbar is set to default value of 1> print> (> 'Standard Deviation of the sample is % s '> > %> (statistics.stdev(sample)))> # variance is approximately the> # squared result of what stdev is> print> (> 'Variance of the sample is % s'> > %> (statistics.variance(sample)))> |
Produzione :
Standard Deviation of the sample is 1.5811388300841898 Variance of the sample is 2.5
Codice n. 4: Dimostrare l'uso di xbar parametro
Python3
# Python code to demonstrate use of xbar> # parameter while using stdev() function> # Importing statistics module> import> statistics> # creating a sample list> sample> => (> 1> ,> 1.3> ,> 1.2> ,> 1.9> ,> 2.5> ,> 2.2> )> # calculating the mean of sample set> m> => statistics.mean(sample)> # xbar is nothing but stores> # the mean of the sample set> # calculating the variance of sample set> print> (> 'Standard Deviation of Sample set is % s'> > %> (statistics.stdev(sample, xbar> => m)))> |
Produzione :
Standard Deviation of Sample set is 0.6047037842337906
Codice n.5: Dimostra l'errore statistico
Python3
# Python code to demonstrate StatisticsError> # importing the statistics module> import> statistics> # creating a data-set with one element> sample> => [> 1> ]> # will raise StatisticsError> print> (statistics.stdev(sample))> |
Produzione :
Traceback (most recent call last): File '/home/f921f9269b061f1cc4e5fc74abf6ce10.py', line 12, in print(statistics.stdev(sample)) File '/usr/lib/python3.5/statistics.py', line 617, in stdev var = variance(data, xbar) File '/usr/lib/python3.5/statistics.py', line 555, in variance raise StatisticsError('variance requires at least two data points') statistics.StatisticsError: variance requires at least two data points Applicazioni:
- La deviazione standard è estremamente essenziale nel campo della matematica statistica e dello studio statistico. È comunemente usato per misurare la fiducia nei calcoli statistici. Ad esempio, il margine di errore nel calcolo del voto di un esame viene determinato calcolando la deviazione standard prevista nei risultati se lo stesso esame dovesse essere ripetuto più volte.
- È molto utile nel campo degli studi finanziari e aiuta a determinare il margine di profitto e perdita. Anche la deviazione standard è importante, dove la deviazione standard del tasso di rendimento di un investimento è una misura della volatilità dell'investimento.