Grafico planare:

Un grafo si dice planare se può essere disegnato su un piano in modo che nessun spigolo si intersechi.
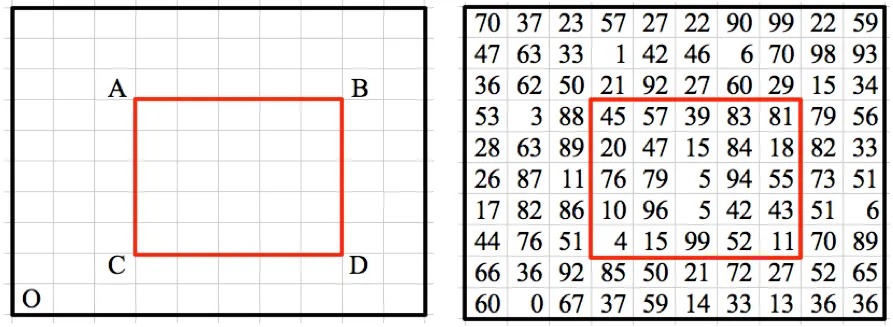
Esempio: Il grafico mostrato in fig è un grafico planare.


Regione di un grafico: Consideriamo un grafo planare G=(V,E). Una regione è definita come un'area del piano delimitata da bordi e non può essere ulteriormente suddivisa. Un grafico planare divide i piani in una o più regioni. Una di queste regioni sarà infinita.
Regione finita: Se l'area della regione è finita, allora quella regione è chiamata regione finita.
Regione infinita: Se l'area della regione è infinita, quella regione viene chiamata regione infinita. Un grafo planare ha una sola regione infinita.
Esempio: Considera il grafico mostrato in Fig. Determina il numero di regioni, regioni finite e una regione infinita.

Soluzione: Ci sono cinque regioni nel grafico sopra, vale a dire r 1 ,R 2 ,R 3 ,R 4 ,R 5 .
Ci sono quattro regioni finite nel grafico, cioè r 2 ,R 3 ,R 4 ,R 5 .
Esiste solo una regione finita, cioè r 1
Proprietà dei grafici planari:
- Se un grafo planare connesso G ha e bordi e r regioni, allora r ≦
 È.
È. - Se un grafo planare connesso G ha e bordi, v vertici e r regioni, allora v-e+r=2.
- Se un grafo planare connesso G ha e bordi e v vertici, allora 3v-e≧6.
- Un grafico completo K N è planare se e solo se n <5. < li>
- Un grafo bipartito completo K mn è planare se e solo se m3.
Esempio: Dimostrare che il grafico completo K 4 è planare.
Soluzione: Il grafico completo K 4 contiene 4 vertici e 6 spigoli.
Sappiamo che per un grafo planare connesso 3v-e≧6. Quindi per K 4 , abbiamo 3x4-6=6 che soddisfa la proprietà (3).
Così K 4 è un grafo planare. Quindi dimostrato.
Grafico non planare:
Un grafo si dice non planare se non può essere disegnato su un piano in modo che nessun spigolo si intersechi.
Esempio: I grafici mostrati in fig sono grafici non planari.

Questi grafici non possono essere disegnati su un piano in modo che nessun bordo si intersechi, quindi sono grafici non planari.
Proprietà dei grafici non planari:
Un grafo è non planare se e solo se contiene un sottografo omeomorfo a K 5 o K 3.3
Esempio 1: Mostra che K 5 non è planare.
Soluzione: Il grafico completo K 5 contiene 5 vertici e 10 spigoli.
Ora, per un grafo planare connesso 3v-e≧6.
Quindi, per K 5 , abbiamo 3 x 5-10=5 (che non soddisfa la proprietà 3 perché deve essere maggiore o uguale a 6).
Così, K 5 è un grafo non planare.
Esempio2: Mostrare che i grafici mostrati in figura non sono planari trovando un sottografo omeomorfo a K 5 o K 3.3 .


Soluzione: Se rimuoviamo i bordi (V 1 ,IN 4 ),(IN 3 ,IN 4 ) e (V 5 ,IN 4 ) il grafico G 1 ,diventa omeomorfo a K 5 .Quindi non è planare.
Se rimuoviamo il bordo V 2, V 7) il grafico G 2 diventa omeomorfo a K 3.3 .Quindi è un non planare.
Colorazione del grafico:
Supponiamo che G= (V,E) sia un grafico senza più archi. Una colorazione dei vertici di G è un'assegnazione di colori ai vertici di G tale che i vertici adiacenti abbiano colori diversi. Un grafo G è M-Colorabile se esiste una colorazione di G che utilizza M-Colori.
Colorazione corretta: Una colorazione è propria se due vertici adiacenti u e v hanno colori diversi altrimenti si dice colorazione impropria.
Esempio: Considera il grafico seguente e colora C={r, w, b, y}. Colora il grafico correttamente utilizzando tutti i colori o meno colori.

Il grafico mostrato in fig è un minimo 3-colorabile, quindi x(G)=3
Soluzione: La Fig mostra il grafico opportunamente colorato con tutti e quattro i colori.

La Fig mostra il grafico opportunamente colorato con tre colori.

Numero cromatico di G: Il numero minimo di colori necessari per produrre una corretta colorazione di un grafico G è chiamato numero cromatico di G ed è indicato con x(G).
Esempio: Il numero cromatico di K N è n.
Soluzione: Una colorazione di K N può essere costruito utilizzando n colori assegnando colori diversi a ciascun vertice. Non è possibile assegnare a due vertici gli stessi colori, poiché ogni due vertici di questo grafico sono adiacenti. Da qui il numero cromatico di K N =n.
Applicazioni della colorazione dei grafici
Alcune applicazioni della colorazione dei grafici includono:
- Registra l'assegnazione
- Colorazione della mappa
- Controllo del grafico bipartito
- Assegnazione della frequenza radiomobile
- Fare un orario, ecc.
Enunciare e dimostrare il teorema dell'handshaking.
Teorema dell'handshake: La somma dei gradi di tutti i vertici in un grafico G è pari al doppio del numero di archi nel grafico.
Matematicamente si può affermare come:
∑ v∈V gradi(v)=2e
Prova: Sia G = (V, E) un grafo dove V = {v 1 ,In 2 , . . . . . . . . . .} l'insieme dei vertici ed E = {e 1 ,È 2 . . . . . . . . . .} sia l'insieme degli spigoli. Sappiamo che ogni bordo si trova tra due vertici, quindi fornisce il primo grado a ciascun vertice. Quindi ciascun bordo contribuisce al grado due del grafico. Quindi la somma dei gradi di tutti i vertici è pari al doppio del numero degli spigoli in G.
Quindi, ∑ v∈V gradi(v)=2e