Segmenti minimi nel display a sette segmenti
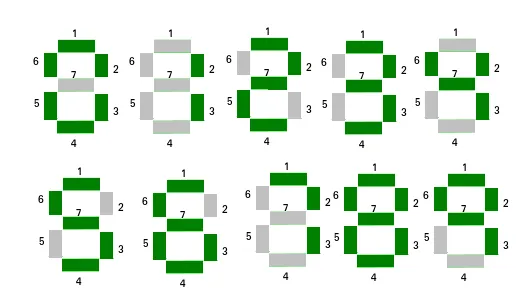
Per visualizzare i numeri è possibile utilizzare un display a sette segmenti. Data una serie di N numeri naturali. Il compito è trovare il numero nell'array che utilizza il numero minimo di segmenti per visualizzare il numero. Se più numeri hanno un numero minimo di segmenti, viene generato il numero con l'indice più piccolo.

Esempi:
Ingresso: arr[] = { 1 2 3 4 5 }.
Produzione : 1
Spiegazione: L'elemento che utilizza il numero minimo di segmenti è 1 (ovvero 2 segmenti)Ingresso: arr[] = { 489 206 745 123 756 }.
Produzione : 745
Spiegazione: L'elemento con l'indice più piccolo che utilizza il numero minimo di segmenti è 745 (ovvero 12 segmenti)
L'idea è di precalcolare il numero di segmenti utilizzati dalle cifre da 0 a 9 e memorizzarlo. Ora per ogni elemento dell'array somma il numero di segmenti utilizzati da ciascuna cifra. Quindi trova l'elemento che utilizza il numero minimo di segmenti.
C++Il numero di segmenti utilizzati dalla cifra:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include using namespace std ; // Precomputed values of segment used by digit 0 to 9. const int seg [ 10 ] = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } int elementMinSegment ( vector < int > arr int n ) { // Initialising the minimum segment and minimum // number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } int main () { vector < int > arr = { 489 206 745 123 756 }; int n = arr . size (); cout < < elementMinSegment ( arr n ) < < endl ; return 0 ; }
Java import java.io.* ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ] ; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ] ; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ] ); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ] ); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ] ; } static public void main ( String [] args ) { int [] arr = { 489 206 745 123 756 }; int n = arr . length ; System . out . println ( elementMinSegment ( arr n )); } }
Python # Precomputed values of segment # used by digit 0 to 9. seg = [ 6 2 5 5 4 5 6 3 7 6 ] # Return the number of # segments used by x. def computeSegment ( x ): if ( x == 0 ): return seg [ 0 ] count = 0 # Finding sum of the segment # used by each digit of a number. while ( x ): count += seg [ x % 10 ] x = x // 10 return count # function to return minimum sum index def elementMinSegment ( arr n ): # Initialising the minimum # segment and minimum number index. minseg = computeSegment ( arr [ 0 ]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range ( 1 n ): temp = computeSegment ( arr [ i ]) # If arr[i] used less segment # then update minimum segment # and minimum number. if ( temp < minseg ): minseg = temp minindex = i return arr [ minindex ] # Driver Code arr = [ 489 206 745 123 756 ] n = len ( arr ) # function print required answer print ( elementMinSegment ( arr n )) # This code is contributed by # Sanjit_Prasad
C# using System ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = new int [ 10 ]{ 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } static public void Main () { int [] arr = { 489 206 745 123 756 }; int n = arr . Length ; Console . WriteLine ( elementMinSegment ( arr n )); } }
JavaScript // Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6 ]; // Return the number of segments used by x. function computeSegment ( x ) { if ( x == 0 ) return seg [ 0 ]; let count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x = parseInt ( x / 10 10 ); } return count ; } function elementMinSegment ( arr n ) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment ( arr [ 0 ]); let minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( let i = 1 ; i < n ; i ++ ) { let temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr . length ; console . log ( elementMinSegment ( arr n ));
Produzione
745
Complessità temporale: O(n * log 10 N)
Spazio ausiliario: O(10)