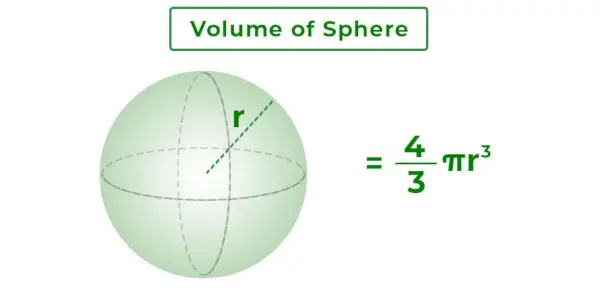
Impara DSA con Python | Strutture dati e algoritmi Python

Questo tutorial è una guida adatta ai principianti apprendimento di strutture dati e algoritmi utilizzando Python. In questo articolo discuteremo delle strutture dati integrate come elenchi, tuple, dizionari, ecc. E di alcune strutture dati definite dall'utente come elenchi collegati , alberi , grafici , ecc., e algoritmi di attraversamento, ricerca e ordinamento con l'aiuto di esempi validi e ben spiegati e domande pratiche.

Elenchi
Elenchi Python sono raccolte ordinate di dati proprio come gli array in altri linguaggi di programmazione. Permette diversi tipi di elementi nell'elenco. L'implementazione di Python List è simile a Vectors in C++ o ArrayList in JAVA. L'operazione costosa è inserire o eliminare l'elemento dall'inizio della Lista poiché è necessario spostare tutti gli elementi. L'inserimento e la cancellazione alla fine della lista possono diventare costosi anche nel caso in cui la memoria preallocata si riempia.
Esempio: creazione dell'elenco Python
Python3 List = [1, 2, 3, 'GFG', 2.3] print(List)
Produzione
[1, 2, 3, 'GFG', 2.3]
È possibile accedere agli elementi dell'elenco tramite l'indice assegnato. Nell'indice iniziale dell'elenco Python, una sequenza è 0 e l'indice finale è (se sono presenti N elementi) N-1.

Esempio: operazioni su elenchi Python
Python3 # Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3]) Produzione
List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks
Tupla
Tuple Python sono simili alle liste ma le tuple lo sono immutabile in natura cioè una volta creato non può essere modificato. Proprio come una Lista, anche una Tupla può contenere elementi di vario tipo.
In Python, le tuple vengono create inserendo una sequenza di valori separati da 'virgola' con o senza l'uso di parentesi per il raggruppamento della sequenza di dati.
Nota: Per creare una tupla di un elemento deve esserci una virgola finale. Ad esempio, (8,) creerà una tupla contenente 8 come elemento.
Esempio: operazioni su tuple Python
Python3 # Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3]) Produzione
Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4 Impostato
Insieme del pitone è una raccolta mutabile di dati che non consente alcuna duplicazione. I set vengono fondamentalmente utilizzati per includere il test di appartenenza e l'eliminazione delle voci duplicate. La struttura dei dati utilizzata in questo caso è l'hashing, una tecnica popolare per eseguire in media l'inserimento, l'eliminazione e l'attraversamento in O(1).
Se sono presenti più valori nella stessa posizione di indice, il valore viene aggiunto a quella posizione di indice per formare un elenco collegato. In, i set CPython vengono implementati utilizzando un dizionario con variabili fittizie, in cui gli esseri chiave vengono impostati dai membri con maggiori ottimizzazioni in base alla complessità temporale.
Imposta implementazione:

Set con numerose operazioni su una singola HashTable:

Esempio: operazioni sugli insiemi di Python
Python3 # Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set) Produzione
Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True Set congelati
Set congelati in Python sono oggetti immutabili che supportano solo metodi e operatori che producono un risultato senza influenzare l'insieme o gli insiemi congelati a cui vengono applicati. Mentre gli elementi di un set possono essere modificati in qualsiasi momento, gli elementi del set congelato rimangono gli stessi dopo la creazione.
Esempio: set Python Frozen
Python3 # Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h') Produzione
Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'}) Corda
Stringhe di Python è l'array immutabile di byte che rappresentano i caratteri Unicode. Python non ha un tipo di dati carattere, un singolo carattere è semplicemente una stringa con una lunghezza pari a 1.
Nota: Poiché le stringhe sono immutabili, la modifica di una stringa comporterà la creazione di una nuova copia.

Esempio: operazioni su stringhe Python
Python3 String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1]) Produzione
Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s
Dizionario
Dizionario Python è una raccolta non ordinata di dati che archivia i dati nel formato della coppia chiave:valore. È come le tabelle hash in qualsiasi altro linguaggio con la complessità temporale di O(1). L'indicizzazione del dizionario Python viene eseguita con l'aiuto delle chiavi. Questi sono di qualsiasi tipo hashable, ovvero un oggetto che non può mai cambiare come stringhe, numeri, tuple, ecc. Possiamo creare un dizionario utilizzando le parentesi graffe ({}) o la comprensione del dizionario.
Esempio: operazioni del dizionario Python
Python3 # Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict) Produzione
Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25} Matrice
Una matrice è un array 2D in cui ogni elemento ha esattamente la stessa dimensione. Per creare una matrice utilizzeremo il file Pacchetto NumPy .
Esempio: operazioni con matrice Python NumPy
Python3 import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m) Produzione
[[ 1 2 3 4] [ 4 55 1 2] [ 8 3 20 19] [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4] [ 4 55 1 2] [ 8 3 20 19] [11 2 22 21] [ 1 15 13 11]] Deleting Element [[ 1 2 3 4] [ 8 3 20 19] [11 2 22 21] [ 1 15 13 11]]
Bytearray
Python Bytearray fornisce una sequenza mutabile di numeri interi nell'intervallo 0 <= x < 256.
Esempio: operazioni su bytearray Python
Python3 # Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a) Produzione
Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')
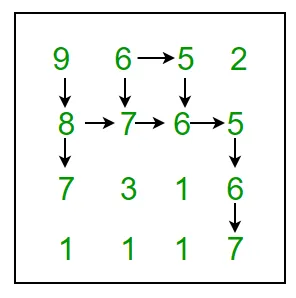
Lista collegata
UN lista collegata è una struttura dati lineare, in cui gli elementi non sono memorizzati in locazioni di memoria contigue. Gli elementi in un elenco collegato sono collegati utilizzando puntatori come mostrato nell'immagine seguente:

Una lista concatenata è rappresentata da un puntatore al primo nodo della lista concatenata. Il primo nodo è chiamato testa. Se l'elenco collegato è vuoto, il valore dell'intestazione è NULL. Ogni nodo in un elenco è composto da almeno due parti:
- Dati
- Puntatore (o riferimento) al nodo successivo
Esempio: definizione di un elenco collegato in Python
Python3 # Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None
Creiamo una semplice lista concatenata con 3 nodi.
Python3 # A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) ''' Three nodes have been created. We have references to these three blocks as head, second and third llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | None | | 2 | None | | 3 | None | +----+------+ +----+------+ +----+------+ ''' llist.head.next = second; # Link first node with second ''' Now next of first Node refers to second. So they both are linked. llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2| nullo | | 3| nullo | +----+------+ +----+------+ +----+------+ ''' secondo.successivo = terzo ; # Collega il secondo nodo con il terzo nodo ''' Ora il successivo del secondo nodo si riferisce al terzo. Quindi tutti e tre i nodi sono collegati. llist.head secondo terzo | | | | | | +----+------+ +----+------+ +----+------+ | 1| o-------->| 2| o-------->| 3| nullo | +----+------+ +----+------+ +----+------+ '''
Attraversamento di elenchi collegati
Nel programma precedente abbiamo creato una semplice lista concatenata con tre nodi. Attraversiamo l'elenco creato e stampiamo i dati di ciascun nodo. Per l'attraversamento, scriviamo una funzione generica printList() che stampa qualsiasi elenco specificato.
Python3 # A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()
Produzione
1 2 3
Altri articoli sull'elenco collegato
- Inserimento di liste collegate
- Eliminazione elenco collegato (eliminazione di una determinata chiave)
- Eliminazione elenco collegato (eliminazione di una chiave in una determinata posizione)
- Trovare la lunghezza di un elenco collegato (iterativo e ricorsivo)
- Cerca un elemento in una lista collegata (iterativo e ricorsivo)
- Nesimo nodo dalla fine di una Lista Collegata
- Invertire un elenco collegato

Le funzioni associate allo stack sono:
- vuoto() - Restituisce se lo stack è vuoto – Complessità temporale: O(1)
- misurare() - Restituisce la dimensione dello stack – Complessità temporale: O(1)
- superiore() - Restituisce un riferimento all'elemento più in alto dello stack – Complessità temporale: O(1)
- spingere(a) – Inserisce l'elemento 'a' in cima allo stack – Complessità temporale: O(1)
- pop() – Elimina l'elemento più in alto dello stack – Complessità temporale: O(1)
stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty Produzione
Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []
Altri articoli su Stack
- Conversione da infisso a suffisso utilizzando Stack
- Conversione da prefisso a infisso
- Conversione da prefisso a suffisso
- Conversione da suffisso a prefisso
- Da suffisso a infisso
- Controlla la presenza di parentesi bilanciate in un'espressione
- Valutazione dell'espressione suffissa
Come pila, il coda è una struttura dati lineare che memorizza gli elementi in modalità FIFO (First In First Out). Con una coda, l'elemento aggiunto meno di recente viene rimosso per primo. Un buon esempio di coda è qualsiasi coda di consumatori per una risorsa in cui il consumatore arrivato per primo viene servito per primo.

Le operazioni associate alla coda sono:
- Accodare: Aggiunge un elemento alla coda. Se la coda è piena, si parla di condizione di Overflow – Complessità temporale: O(1)
- Di conseguenza: Rimuove un elemento dalla coda. Gli elementi vengono estratti nello stesso ordine in cui vengono inseriti. Se la coda è vuota, si parla di condizione di underflow – Complessità temporale: O(1)
- Davanti: Ottieni l'elemento in primo piano dalla coda – Complessità temporale: O(1)
- Posteriore: Ottieni l'ultimo elemento dalla coda – Complessità temporale: O(1)
# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty Produzione
Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []
Altri articoli su Coda
- Implementa la coda utilizzando gli stack
- Implementa lo stack utilizzando le code
- Implementa uno stack utilizzando una coda singola
Coda prioritaria
Code prioritarie sono strutture di dati astratte in cui ogni dato/valore in coda ha una certa priorità. Ad esempio, nelle compagnie aeree, i bagagli con il titolo Business o First class arrivano prima degli altri. Priority Queue è un'estensione della coda con le seguenti proprietà.
- Un elemento con priorità alta viene rimosso dalla coda prima di un elemento con priorità bassa.
- Se due elementi hanno la stessa priorità, verranno serviti secondo il loro ordine in coda.
# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] return item eccetto IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) while not myQueue.isEmpty(): print(myQueue.delete())
Produzione
12 1 14 7 14 12 7 1
Mucchio
modulo heapq in Python fornisce la struttura dei dati heap utilizzata principalmente per rappresentare una coda con priorità. La proprietà di questa struttura dati è che fornisce sempre l'elemento più piccolo (heap minimo) ogni volta che l'elemento viene estratto. Ogni volta che gli elementi vengono spinti o estratti, la struttura dell'heap viene mantenuta. L'elemento heap[0] restituisce ogni volta anche l'elemento più piccolo. Supporta l'estrazione e l'inserimento dell'elemento più piccolo nei tempi O(log n).
Generalmente gli Heap possono essere di due tipi:
- Heap massimo: In un Max-Heap la chiave presente nel nodo radice deve essere la maggiore tra le chiavi presenti in tutti i suoi figli. La stessa proprietà deve essere vera ricorsivamente per tutti i sottoalberi di quell'albero binario.
- Heap minimo: In un Min-Heap la chiave presente nel nodo radice deve essere minima tra le chiavi presenti in tutti i suoi figli. La stessa proprietà deve essere vera ricorsivamente per tutti i sottoalberi di quell'albero binario.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li)) Produzione
The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1
Altri articoli su Heap
- Heap binario
- K'esimo elemento più grande in un array
- K'esimo elemento più piccolo/più grande nell'array non ordinato
- Ordina un array quasi ordinato
- K-esimo sottoarray contiguo con somma più grande
- Somma minima di due numeri formati da cifre di un array
Un albero è una struttura di dati gerarchica simile alla figura seguente:
tree ---- j <-- root / f k / a h z <-- leaves
Il nodo più in alto dell'albero è chiamato radice mentre i nodi più in basso o i nodi senza figli sono chiamati nodi foglia. I nodi che sono direttamente sotto un nodo sono chiamati i suoi figli e i nodi che sono direttamente sopra qualcosa sono chiamati il suo genitore.
UN albero binario è un albero i cui elementi possono avere quasi due figli. Poiché ogni elemento in un albero binario può avere solo 2 figli, in genere li chiamiamo figlio sinistro e figlio destro. Un nodo di albero binario contiene le seguenti parti.
- Dati
- Puntatore al bambino sinistro
- Puntatore al bambino giusto
Esempio: definizione della classe del nodo
Python3 # A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key
Ora creiamo un albero con 4 nodi in Python. Supponiamo che la struttura ad albero sia simile alla seguente:
tree ---- 1 <-- root / 2 3 / 4
Esempio: aggiunta di dati all'albero
Python3 # Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement 1 / None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1 1 / 2 3 / / None None None None''' root.left.left = Node(4); '''4 becomes left child of 2 1 / 2 3 / / 4 None None None / None None'''
Attraversamento degli alberi
Gli alberi possono essere attraversati in diversi modi. Di seguito sono riportati i modi generalmente utilizzati per attraversare gli alberi. Consideriamo l'albero sottostante:
tree ---- 1 <-- root / 2 3 / 4 5
Prime traversate in profondità:
- In ordine (Sinistra, Radice, Destra): 4 2 5 1 3
- Preordine (radice, sinistra, destra): 1 2 4 5 3
- Postorder (Sinistra, Destra, Radice): 4 5 2 3 1
Algoritmo in ordine (albero)
- Attraversa il sottoalbero sinistro, ovvero chiama Inorder(left-subtree)
- Visita la radice.
- Attraversa il sottoalbero destro, ovvero chiama Inorder(right-subtree)
Preordine dell'algoritmo (albero)
- Visita la radice.
- Attraversa il sottoalbero sinistro, ovvero chiama Preorder(left-subtree)
- Attraversa il sottoalbero destro, ovvero chiama Preorder(right-subtree)
Algoritmo Vaglia postale(albero)
- Attraversa il sottoalbero sinistro, ovvero chiama Postorder(sottoalbero sinistro)
- Attraversa il sottoalbero destro, ovvero chiama Postorder(right-subtree)
- Visita la radice.
# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root) Produzione
Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1
Complessità temporale – O(n)
Attraversamento dell'ordine di ampiezza o di livello
Attraversamento dell'ordine di livello di un albero è l'attraversamento in ampiezza per l'albero. L'attraversamento dell'ordine di livello dell'albero sopra è 1 2 3 4 5.
Per ciascun nodo, prima viene visitato il nodo e poi i suoi nodi figli vengono inseriti in una coda FIFO. Di seguito è riportato l'algoritmo per lo stesso:
- Creare una coda vuota q
- nodo_temp = root /*inizia da root*/
- Ciclo mentre temp_node non è NULL
- stampa nodo_temp->dati.
- Accoda i figli di temp_node (prima quelli a sinistra, poi quelli a destra) a q
- Togliere dalla coda un nodo da q
# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Stampa la parte anteriore della coda e # la rimuove dalla coda print (queue[0].data) node = Queue.pop(0) # Accoda il figlio sinistro se node.left non è Nessuno: Queue.append(node.left ) # Accoda il figlio destro se node.right non è Nessuno: tail.append(node.right) # Programma driver per testare la funzione precedente root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('L'attraversamento dell'ordine di livello dell'albero binario è -') printLevelOrder(root) Produzione
Level Order Traversal of binary tree is - 1 2 3 4 5
Complessità temporale: O(n)
Altri articoli sull'albero binario
- Inserimento in un albero binario
- Cancellazione in un albero binario
- Attraversamento dell'albero in ordine senza ricorsione
- Attraversamento dell'albero in ordine senza ricorsione e senza stack!
- Stampa l'attraversamento Postorder da determinati attraversamenti Inorder e Preorder
- Trova l'attraversamento postordine della BST dall'attraversamento preordine
- Il sottoalbero sinistro di un nodo contiene solo nodi con chiavi inferiori alla chiave del nodo.
- Il sottoalbero destro di un nodo contiene solo nodi con chiavi maggiori della chiave del nodo.
- Anche i sottoalberi sinistro e destro devono essere un albero di ricerca binario.

Le proprietà di cui sopra dell'albero di ricerca binario forniscono un ordinamento tra le chiavi in modo che le operazioni come ricerca, minimo e massimo possano essere eseguite rapidamente. Se non c'è ordine, potremmo dover confrontare ogni chiave per cercare una determinata chiave.
Elemento di ricerca
- Inizia dalla radice.
- Confronta l'elemento da cercare con root, se minore di root, quindi ricorsivo per sinistra, altrimenti ricorsivo per destra.
- Se l'elemento da cercare si trova ovunque, restituisce true, altrimenti restituisce false.
# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)
Inserimento di una chiave
- Inizia dalla radice.
- Confronta l'elemento di inserimento con root, se minore di root, quindi ricorsivo per sinistra, altrimenti ricorsivo per destra.
- Dopo aver raggiunto la fine, inserisci semplicemente quel nodo a sinistra (se inferiore a quello corrente) altrimenti a destra.
# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # / # 30 70 # / / # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)
Produzione
20 30 40 50 60 70 80
Altri articoli sull'albero di ricerca binaria
- Albero di ricerca binario: chiave Elimina
- Costruisci BST da un dato attraversamento del preordine | Insieme 1
- Conversione da albero binario a albero di ricerca binario
- Trova il nodo con il valore minimo in un albero di ricerca binario
- Un programma per verificare se un albero binario è BST o meno
UN grafico è una struttura dati non lineare costituita da nodi e spigoli. I nodi sono talvolta indicati anche come vertici e gli spigoli sono linee o archi che collegano due nodi qualsiasi nel grafico. Più formalmente un grafico può essere definito come un grafico costituito da un insieme finito di vertici (o nodi) e un insieme di archi che collegano una coppia di nodi.

Nel grafico sopra, l'insieme dei vertici V = {0,1,2,3,4} e l'insieme degli archi E = {01, 12, 23, 34, 04, 14, 13}. Le due seguenti sono le rappresentazioni più comunemente utilizzate di un grafico.
- Matrice di adiacenza
- Elenco delle adiacenze
Matrice di adiacenza
La matrice di adiacenza è una matrice 2D di dimensione V x V dove V è il numero di vertici in un grafico. Sia l'array 2D adj[][], uno slot adj[i][j] = 1 indica che esiste un bordo dal vertice i al vertice j. La matrice di adiacenza per un grafo non orientato è sempre simmetrica. La matrice di adiacenza viene utilizzata anche per rappresentare grafici ponderati. Se adj[i][j] = w, allora esiste un arco dal vertice i al vertice j con peso w.
Python3 # A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0 <=vtx <=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix()) Produzione
Vertici del grafico
['a B c D e F']
Bordi del grafico
[('a', 'c', 20), ('a', 'e', 10), ('b', 'c', 30), ('b', 'e', 40), ( 'c', 'a', 20), ('c', 'b', 30), ('d', 'e', 50), ('e', 'a', 10), ('e ', 'b', 40), ('e', 'd', 50), ('e', 'f', 60), ('f', 'e', 60)]
Matrice di adiacenza del grafico
[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]
Elenco delle adiacenze
Viene utilizzata una serie di elenchi. La dimensione dell'array è uguale al numero di vertici. Lascia che l'array sia un array[]. Una voce array[i] rappresenta l'elenco dei vertici adiacenti all'i-esimo vertice. Questa rappresentazione può essere utilizzata anche per rappresentare un grafico ponderato. I pesi degli archi possono essere rappresentati come elenchi di coppie. Di seguito è riportata la rappresentazione dell'elenco di adiacenza del grafico sopra.

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print('
') # Programma driver per la classe del grafico sopra if __name__ == '__main__' : V = 5 grafico = Grafico(V) grafico.add_edge(0, 1) grafico.add_edge(0, 4) grafico.add_edge(1, 2) grafico.add_edge(1, 3) grafico.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph() Produzione
Adjacency list of vertex 0 head ->4 -> 1 Elenco di adiacenze della testa del vertice 1 -> 4 -> 3 -> 2 -> 0 Elenco di adiacenze della testa del vertice 2 -> 3 -> 1 Elenco di adiacenze della testa del vertice 3 -> 4 -> 2 -> 1 Adiacenza elenco dei vertici 4 testa -> 3 -> 1 -> 0
Attraversamento del grafico
Ricerca in ampiezza o BFS
Traversata in ampiezza poiché un grafico è simile all'attraversamento in larghezza di un albero. L'unico problema qui è che, a differenza degli alberi, i grafici possono contenere cicli, quindi potremmo ritrovarci di nuovo sullo stesso nodo. Per evitare di elaborare un nodo più di una volta, utilizziamo un array visitato booleano. Per semplicità si assume che tutti i vertici siano raggiungibili dal vertice iniziale.
Ad esempio, nel grafico seguente, iniziamo l'attraversamento dal vertice 2. Quando arriviamo al vertice 0, cerchiamo tutti i suoi vertici adiacenti. 2 è anche un vertice adiacente di 0. Se non contrassegniamo i vertici visitati, 2 verrà elaborato nuovamente e diventerà un processo non terminato. Una traversata in ampiezza del grafico seguente è 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2) Produzione
Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1
Complessità temporale: O(V+E) dove V è il numero di vertici nel grafico ed E è il numero di archi nel grafico.
Prima ricerca in profondità o DFS
Prima traversata in profondità per un grafico è simile alla prima traversata in profondità di un albero. L'unico problema qui è che, a differenza degli alberi, i grafici possono contenere cicli e un nodo può essere visitato due volte. Per evitare di elaborare un nodo più di una volta, utilizzare un array visitato booleano.
Algoritmo:
- Crea una funzione ricorsiva che accetta l'indice del nodo e un array visitato.
- Contrassegna il nodo corrente come visitato e stampa il nodo.
- Attraversa tutti i nodi adiacenti e non contrassegnati e chiama la funzione ricorsiva con l'indice del nodo adiacente.
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2) Produzione
Following is DFS from (starting from vertex 2) 2 0 1 3
Altri articoli sul grafico
- Rappresentazioni grafiche utilizzando set e hash
- Trova il vertice madre in un grafico
- Prima ricerca iterativa della profondità
- Conta il numero di nodi a un dato livello in un albero usando BFS
- Conta tutti i percorsi possibili tra due vertici
Il processo in cui una funzione richiama se stessa direttamente o indirettamente si chiama ricorsione e la funzione corrispondente si chiama a funzione ricorsiva . Utilizzando gli algoritmi ricorsivi, alcuni problemi possono essere risolti abbastanza facilmente. Esempi di tali problemi sono Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, ecc.
Qual è la condizione di base nella ricorsione?
Nel programma ricorsivo viene fornita la soluzione del caso base e la soluzione del problema più grande viene espressa in termini di problemi più piccoli.
def fact(n): # base case if (n <= 1) return 1 else return n*fact(n-1)
Nell'esempio sopra, è definito il caso base per n <= 1 e il valore più grande del numero può essere risolto convertendolo in uno più piccolo fino al raggiungimento del caso base.
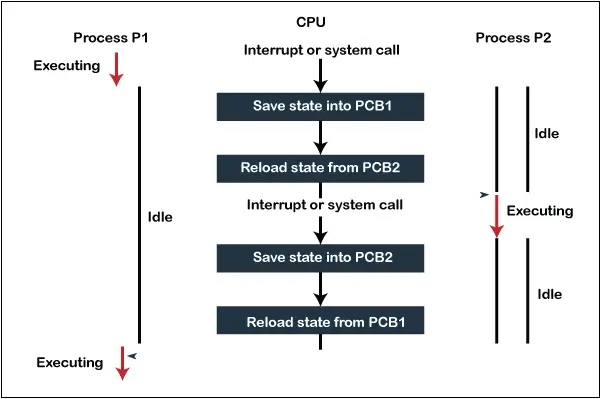
Come viene allocata la memoria alle diverse chiamate di funzione in ricorsione?
Quando una funzione viene chiamata da main(), la memoria le viene allocata nello stack. Una funzione ricorsiva chiama se stessa, la memoria per una funzione chiamata viene allocata sopra la memoria allocata alla funzione chiamante e viene creata una copia diversa delle variabili locali per ogni chiamata di funzione. Quando viene raggiunto il caso base, la funzione restituisce il suo valore alla funzione da cui è stata chiamata, la memoria viene deallocata e il processo continua.
Prendiamo l'esempio di come funziona la ricorsione prendendo una semplice funzione.
Python3 # A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)
Produzione
3 2 1 1 2 3
Lo stack di memoria è stato mostrato nel diagramma seguente.

Altri articoli sulla ricorsione
- Ricorsione
- Ricorsione in Python
- Domande pratiche per la ricorsione | Insieme 1
- Domande pratiche per la ricorsione | Insieme 2
- Domande pratiche per la ricorsione | Insieme 3
- Domande pratiche per la ricorsione | Insieme 4
- Domande pratiche per la ricorsione | Insieme 5
- Domande pratiche per la ricorsione | Insieme 6
- Domande pratiche per la ricorsione | Insieme 7
>>> Altro
Programmazione dinamica
Programmazione dinamica è principalmente un'ottimizzazione sulla ricorsione semplice. Ovunque vediamo una soluzione ricorsiva che ha ripetute chiamate per gli stessi input, possiamo ottimizzarla utilizzando la programmazione dinamica. L'idea è semplicemente di memorizzare i risultati dei sottoproblemi, in modo da non doverli ricalcolare quando necessario in seguito. Questa semplice ottimizzazione riduce le complessità temporali da esponenziale a polinomiale. Ad esempio, se scriviamo una soluzione ricorsiva semplice per i numeri di Fibonacci, otteniamo una complessità temporale esponenziale e se la ottimizziamo memorizzando soluzioni di sottoproblemi, la complessità temporale si riduce a lineare.

Tabulazione vs Memoizzazione
Esistono due modi diversi per memorizzare i valori in modo che i valori di un sottoproblema possano essere riutilizzati. Qui, discuteremo due modelli per risolvere il problema della programmazione dinamica (DP):
- Tabulazione: Dal basso verso l'alto
- Memoizzazione: Dall'alto al basso
Tabulazione
Come suggerisce il nome stesso, partire dal basso e accumulare risposte verso l'alto. Discutiamo in termini di transizione statale.
Descriviamo uno stato per il nostro problema DP che sia dp[x] con dp[0] come stato base e dp[n] come stato di destinazione. Quindi, dobbiamo trovare il valore dello stato di destinazione, ovvero dp[n].
Se iniziamo la nostra transizione dal nostro stato di base, ovvero dp[0] e seguiamo la nostra relazione di transizione di stato per raggiungere il nostro stato di destinazione dp[n], lo chiameremo approccio Bottom-Up poiché è abbastanza chiaro che abbiamo iniziato la nostra transizione dal stato base inferiore e ha raggiunto lo stato desiderato più in alto.
Ora, perché lo chiamiamo metodo di tabulazione?
Per saperlo, scriviamo prima del codice per calcolare il fattoriale di un numero utilizzando l'approccio dal basso verso l'alto. Ancora una volta, come procedura generale per risolvere un DP, definiamo prima uno stato. In questo caso, definiamo uno stato come dp[x], dove dp[x] serve a trovare il fattoriale di x.
Ora è abbastanza ovvio che dp[x+1] = dp[x] * (x+1)
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1): dp[i] = dp[i-1] * i
Memoizzazione
Ancora una volta descriviamolo in termini di transizione di stato. Se dobbiamo trovare il valore per qualche stato diciamo dp[n] e invece di partire dallo stato base cioè dp[0] chiediamo la nostra risposta agli stati che possono raggiungere lo stato di destinazione dp[n] seguendo la transizione di stato relazione, allora è la moda top-down della DP.
Qui iniziamo il nostro viaggio dallo stato di destinazione più in alto e calcoliamo la sua risposta prendendo in considerazione i valori degli stati che possono raggiungere lo stato di destinazione, fino a raggiungere lo stato di base più in basso.
Ancora una volta, scriviamo il codice per il problema fattoriale procedendo dall’alto verso il basso
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x): if (x==0) return 1 if (dp[x]!=-1) return dp[x] return (dp[x] = x * solve(x-1))

Altri articoli sulla programmazione dinamica
- Proprietà ottimale della sottostruttura
- Proprietà dei sottoproblemi sovrapposti
- Numeri di Fibonacci
- Sottoinsieme con somma divisibile per m
- Sottosequenza crescente della somma massima
- Sottostringa comune più lunga
Algoritmi di ricerca
Ricerca lineare
- Inizia dall'elemento più a sinistra di arr[] e uno per uno confronta x con ciascun elemento di arr[]
- Se x corrisponde a un elemento, restituisce l'indice.
- Se x non corrisponde a nessuno degli elementi, restituisce -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result) Produzione
Element is present at index 3
La complessità temporale dell'algoritmo di cui sopra è O(n).
Per ulteriori informazioni, fare riferimento a Ricerca lineare .
Ricerca binaria
Cerca un array ordinato dividendo ripetutamente l'intervallo di ricerca a metà. Inizia con un intervallo che copra l'intero array. Se il valore della chiave di ricerca è inferiore all'elemento al centro dell'intervallo, restringere l'intervallo alla metà inferiore. Altrimenti restringilo alla metà superiore. Controllare ripetutamente finché non viene trovato il valore o l'intervallo è vuoto.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Se l'elemento è presente al centro stesso if arr[mid] == x: return mid # Se l'elemento è più piccolo di mid, allora # può essere presente solo nel sottoarray sinistro elif arr[mid]> x: return ricercabinaria(arr, l, mid-1, x) # Altrimenti l'elemento può essere presente solo # nel sottoarray destro else: return ricercabinaria(arr, mid + 1, r, x ) altrimenti: # L'elemento non è presente nell'array return -1 # Codice driver arr = [ 2, 3, 4, 10, 40 ] x = 10 # Risultato della chiamata di funzione = BinarySearch(arr, 0, len(arr)-1 , x) if risultato != -1: print ('Elemento presente nell'indice % d' % risultato) else: print ('Elemento non presente nell'array') Produzione
Element is present at index 3
La complessità temporale dell'algoritmo di cui sopra è O(log(n)).
Per ulteriori informazioni, fare riferimento a Ricerca binaria .
Algoritmi di ordinamento
Ordinamento selezione
IL ordinamento della selezione L'algoritmo ordina un array trovando ripetutamente l'elemento minimo (considerando l'ordine crescente) dalla parte non ordinata e ponendolo all'inizio. In ogni iterazione dell'ordinamento di selezione, l'elemento minimo (considerando l'ordine crescente) dal sottoarray non ordinato viene selezionato e spostato nel sottoarray ordinato.
Diagramma di flusso dell'ordinamento di selezione:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Scambia l'elemento minimo trovato con # il primo elemento A[i], A[min_idx] = A[min_idx], A[i] # Codice driver da testare sopra print ('Array ordinato ') for i in range(len(A)): print('%d' %A[i]), Produzione
Sorted array 11 12 22 25 64
Complessità temporale: SU 2 ) poiché ci sono due cicli nidificati.
Spazio ausiliario: O(1)
Ordinamento a bolle
Ordinamento a bolle è l'algoritmo di ordinamento più semplice che funziona scambiando ripetutamente gli elementi adiacenti se sono nell'ordine sbagliato.
Illustrazione :

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Codice driver da testare sopra arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('L'array ordinato è:') for i in range(len(arr)): print ('%d' %arr[i]), Produzione
Sorted array is: 11 12 22 25 34 64 90
Complessità temporale: SU 2 )
Ordinamento per inserimento
Per ordinare un array di dimensione n in ordine crescente utilizzando ordinamento di inserimento :
- Itera da arr[1] a arr[n] sull'array.
- Confronta l'elemento corrente (chiave) con il suo predecessore.
- Se l'elemento chiave è più piccolo del suo predecessore, confrontalo con gli elementi precedenti. Sposta gli elementi maggiori di una posizione verso l'alto per fare spazio all'elemento scambiato.
Illustrazione:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 e chiave < arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i]) Produzione
5 6 11 12 13
Complessità temporale: SU 2 ))
Unisci ordinamento
Come QuickSort, Unisci ordinamento è un algoritmo Dividi e Impera. Divide l'array di input in due metà, chiama se stesso per le due metà e quindi unisce le due metà ordinate. La funzione merge() viene utilizzata per unire due metà. Il merge(arr, l, m, r) è un processo chiave che presuppone che arr[l..m] e arr[m+1..r] siano ordinati e unisce i due sottoarray ordinati in uno solo.
MergeSort(arr[], l, r) If r>l 1. Trova il punto centrale per dividere l'array in due metà: middle m = l+ (r-l)/2 2. Richiama mergeSort per la prima metà: richiama mergeSort(arr, l, m) 3. Richiama mergeSort per la seconda metà: richiama mergeSort(arr, m+1, r) 4. Unisci le due metà ordinate nei passaggi 2 e 3: chiama merge(arr, l, m, r)
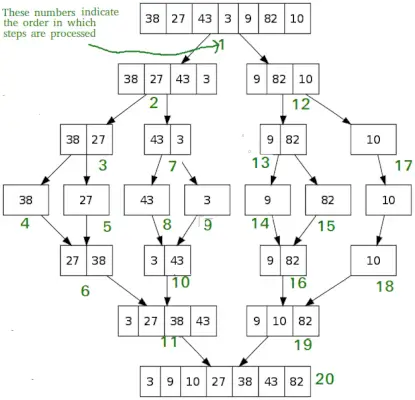
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Trovare la metà dell'array mid = len(arr)//2 # Dividere gli elementi dell'array L = arr[:mid] # in 2 metà R = arr[mid:] # Ordinare la prima metà mergeSort(L) # Ordina la seconda metà mergeSort(R) i = j = k = 0 # Copia i dati negli array temporanei L[] e R[] while i < len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr) Produzione
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13
Complessità temporale: O(n(log))
Ordinamento rapido
Come Unisci ordinamento, Ordinamento rapido è un algoritmo Dividi e Impera. Seleziona un elemento come pivot e suddivide l'array specificato attorno al pivot selezionato. Esistono molte versioni diverse di quickSort che scelgono il pivot in modi diversi.
Scegli sempre il primo elemento come pivot.
- Scegli sempre l'ultimo elemento come pivot (implementato di seguito)
- Scegli un elemento casuale come pivot.
- Scegli la mediana come perno.
Il processo chiave in quickSort è partizione(). L'obiettivo delle partizioni è, dato un array e un elemento x dell'array come pivot, inserire x nella sua posizione corretta nell'array ordinato e inserire tutti gli elementi più piccoli (minori di x) prima di x e inserire tutti gli elementi maggiori (maggiori di x) dopo X. Tutto questo dovrebbe essere fatto in tempo lineare.
/* low -->Indice iniziale, high --> Indice finale */ quickSort(arr[], low, high) { if (low { /* pi è l'indice di partizionamento, arr[pi] ora è al posto giusto */ pi = partizione(arr, basso, alto); quickSort(arr, basso, pi - 1); // Prima di pi rapidoSort(arr, pi + 1, alto); 
Algoritmo di partizione
Possono esserci molti modi per eseguire la partizione, di seguito pseudocodice adotta il metodo riportato nel libro CLRS. La logica è semplice, iniziamo dall'elemento più a sinistra e teniamo traccia dell'indice degli elementi più piccoli (o uguali a) come i. Durante l'attraversamento, se troviamo un elemento più piccolo, scambiamo l'elemento corrente con arr[i]. Altrimenti ignoriamo l'elemento corrente.
pivot: end -= 1 # Se start e end non si sono incrociati, # scambia i numeri su start e end if(start < end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}') Produzione
Sorted array: [1, 5, 7, 8, 9, 10]
Complessità temporale: O(n(log))
ShellSort
ShellSort è principalmente una variazione dell'Insertion Sort. Nell'ordinamento per inserzione, spostiamo gli elementi solo una posizione avanti. Quando un elemento deve essere spostato molto in avanti, sono coinvolti molti movimenti. L'idea di shellSort è quella di consentire lo scambio di elementi lontani. In shellSort, creiamo l'array ordinato in h per un valore elevato di h. Continuiamo a ridurre il valore di h finché non diventa 1. Un array si dice ordinato h se tutte le sottoliste di ogni h th l'elemento è ordinato.
Python3 # Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = gap # controlla l'array da sinistra a destra # fino all'ultimo indice possibile di j while j < len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # ora guardiamo indietro dall'iesimo indice a sinistra # invertiamo i valori che non sono nell'ordine giusto. k = i while k - gap> -1: if arr[k - gap]> arr[k]: arr[k-gap],arr[k] = arr[k],arr[k-gap] k -= 1 gap //= 2 # driver per controllare il codice arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2) Produzione
input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54]
Complessità temporale: SU 2 ).