Introduzione degli automi finiti
Finite Automata (FA) è la macchina più semplice per riconoscere modelli. Viene utilizzato per caratterizzare un linguaggio regolare, ad esempio: /baa+!/.
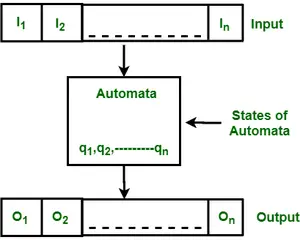
Inoltre viene utilizzato per analizzare e riconoscere le espressioni del linguaggio naturale. Gli automi finiti o macchine a stati finiti sono una macchina astratta che ha cinque elementi o tuple. Ha una serie di stati e regole per passare da uno stato all'altro ma dipende dal simbolo di input applicato. In base agli stati e all'insieme di regole la stringa di input può essere accettata o rifiutata. Fondamentalmente, è un modello astratto di un computer digitale che legge una stringa di input e cambia il suo stato interno a seconda del simbolo di input corrente. Ogni automa definisce un linguaggio, cioè l'insieme di stringhe che accetta. La figura seguente mostra alcune caratteristiche essenziali dell'automazione generale.

Figura: Caratteristiche degli automi finiti
La figura sopra mostra le seguenti caratteristiche degli automi:
- Ingresso
- Produzione
- Stati degli automi
- Rapporto statale
- Relazione di uscita
Un automa finito è costituito da quanto segue:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.
La specifica formale della macchina è
{ Q, ?, q, F, ? } La FA è caratterizzata in due tipologie:
1) Automi finiti deterministici (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->D. In un DFA, per un particolare carattere di input, la macchina va in uno solo stato. Una funzione di transizione è definita su ogni stato per ogni simbolo di input. Inoltre in DFA lo spostamento nullo (o ?) non è consentito, ovvero DFA non può cambiare stato senza alcun carattere di input.
Ad esempio, costruisci un DFA che accetti un linguaggio di tutte le stringhe che terminano con 'a'.
Dato: ? = {a,b}, q = {q 0 }, F={q 1 }, Q = {q 0 , Q 1 }
Innanzitutto, considera un insieme linguistico di tutte le possibili stringhe accettabili per costruire un diagramma accurato delle transizioni di stato.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, padre, padre, padre, padre}
Sopra c'è un semplice sottoinsieme delle possibili stringhe accettabili, ci possono essere molte altre stringhe che terminano con 'a' e contengono simboli {a,b}.
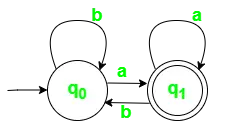
Fig 1. Diagramma di transizione di stato per DFA con ? = {a, b}
Le stringhe non accettate sono,
ab, bb, aab, abbb, ecc.
Tabella di transizione dello stato per l'automa di cui sopra,
| ?Stato Simbolo? | UN | B |
|---|---|---|
| Q 0 | Q 1 | Q 0 |
| Q 1 | Q 1 | Q 0 |
Una cosa importante da notare è, possono esserci molti DFA possibili per un modello . In genere è preferibile un DFA con un numero minimo di Stati.
2) Automi finiti non deterministici (NFA): NFA è simile a DFA ad eccezione delle seguenti funzionalità aggiuntive:
- È consentita la mossa nulla (o ?), ovvero è possibile avanzare senza leggere i simboli.
- Capacità di trasmettere a qualsiasi numero di stati per un particolare input.
Tuttavia, queste funzionalità di cui sopra non aggiungono alcun potere a NFA. Se confrontiamo entrambi in termini di potenza, entrambi sono equivalenti.
A causa delle funzionalità aggiuntive di cui sopra, NFA ha una funzione di transizione diversa, il resto è uguale a DFA.
?: Transition Function ?: Q X (? U ? ) -->2^Q.
Come puoi vedere nella funzione di transizione per qualsiasi input incluso null (o ?), NFA può andare a qualsiasi numero di stati. Ad esempio, di seguito è riportato un NFA per il problema di cui sopra.
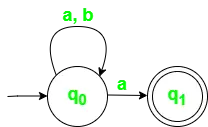
Fig 2. Diagramma di transizione di stato per NFA con ? = {a, b}
Tabella di transizione dello stato per l'automa sopra,
| ?Stato Simbolo? | UN | B |
|---|---|---|
| Q 0 | {Q 0 ,Q 1 } | Q 0 |
| Q 1 | ? | ? |
Una cosa importante da notare è, in NFA, se qualsiasi percorso per una stringa di input porta a uno stato finale, allora la stringa di input È accettato . Ad esempio, nell'NFA precedente, sono presenti più percorsi per la stringa di input 00. Poiché uno dei percorsi porta a uno stato finale, 00 viene accettato dall'NFA precedente.
Alcuni punti importanti:
- Giustificazione:
In case of DFA ? : Q X ? -->D In caso di NFA? : QX? --> 2Q
Ora se osservi scoprirai Q X ? –> Q fa parte di Q X ? –>2 Q .
Sul lato destro, Q è il sottoinsieme di 2 Q che indica che Q è contenuto in 2 Q oppure Q è una parte di 2 Q , tuttavia, non è vero il contrario. Quindi, matematicamente, possiamo concludere questo ogni DFA è NFA ma non viceversa . Eppure esiste un modo per convertire un NFA in DFA, quindi esiste un DFA equivalente per ogni NFA .
- Sia NFA che DFA hanno lo stesso potere e ogni NFA può essere tradotto in un DFA.
- Possono esserci più stati finali sia in DFA che in NFA.
- L'NFA è più un concetto teorico.
- DFA viene utilizzato nell'analisi lessicale nel compilatore.
- Se il numero di stati nella NFA è N, il suo DFA può averne al massimo 2 N numero di stati.
Vedere Quiz sulle espressioni regolari e sugli automi finiti.