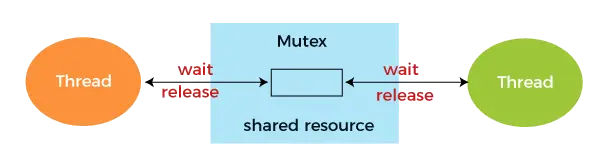
Simile a Queue è una struttura di dati lineare che segue un ordine particolare in cui vengono eseguite le operazioni per la memorizzazione dei dati. L'ordine è il primo a entrare, il primo a uscire (FIFO) . Si può immaginare una coda come una fila di persone in attesa di ricevere qualcosa in ordine sequenziale che inizia dall'inizio della fila. Si tratta di un elenco ordinato in cui gli inserimenti vengono effettuati da un'estremità, detta posteriore, e le eliminazioni dall'altra estremità, detta anteriore. Un buon esempio di coda è qualsiasi coda di consumatori per una risorsa in cui il consumatore arrivato per primo viene servito per primo.
La differenza tra stack e code sta nella rimozione. In uno stack rimuoviamo l'elemento aggiunto più recentemente; in coda, rimuoviamo l'elemento aggiunto meno di recente.

Pratica consigliataImplementa la coda utilizzando l'arrayProvalo!

Struttura dei dati della coda

Operazioni di base sulla coda:

enqueue(): inserisce un elemento alla fine della coda, cioè nella parte posteriore. dequeue(): questa operazione rimuove e restituisce un elemento che si trova all'inizio della coda. front(): questa operazione restituisce l'elemento al front-end senza rimuoverlo. Rear(): questa operazione restituisce l'elemento all'estremità posteriore senza rimuoverlo. isEmpty(): questa operazione indica se la coda è vuota o meno. isFull(): questa operazione indica se la coda è piena o meno. size(): questa operazione restituisce la dimensione della coda, ovvero il numero totale di elementi in essa contenuti.

Tipi di code:

Coda semplice: la coda semplice, nota anche come coda lineare, è la versione più semplice di una coda. In questo caso, l'inserimento di un elemento, ovvero l'operazione di accodamento, avviene nella parte posteriore e la rimozione di un elemento, ovvero l'operazione di rimozione della coda avviene nella parte anteriore. Qui il problema è che se estraiamo alcuni elementi dalla parte anteriore e poi da quelli posteriori raggiungiamo la capacità della coda e sebbene ci siano spazi vuoti prima della parte anteriore significa che la coda non è piena ma come da condizione nella funzione isFull(), mostrerà che la coda è piena allora. Per risolvere questo problema utilizziamo la coda circolare.
• Coda circolare : In una coda circolare, gli elementi della coda fungono da anello circolare. Il funzionamento di una coda circolare è simile a quello della coda lineare tranne per il fatto che l'ultimo elemento è collegato al primo elemento. Il suo vantaggio è che la memoria viene utilizzata in modo migliore. Questo perché se c'è uno spazio vuoto, cioè se non è presente alcun elemento in una determinata posizione nella coda, allora è possibile aggiungere facilmente un elemento in quella posizione utilizzando modulo capacità( %N ).
• Coda prioritaria : Questa coda è un tipo speciale di coda. La sua specialità è che dispone gli elementi in coda in base ad una certa priorità. La priorità può essere qualcosa in cui l'elemento con il valore più alto ha la priorità, quindi crea una coda con un ordine di valori decrescente. La priorità può anche essere tale che l'elemento con il valore più basso ottenga la priorità più alta, quindi a sua volta crea una coda con ordine crescente di valori. Nella coda con priorità predefinita, C++ dà la priorità al valore più alto mentre Java dà la priorità al valore più basso.
• Di conseguenza : La rimozione dalla coda è nota anche come coda a doppio attacco. Come suggerisce il nome double ended, significa che un elemento può essere inserito o rimosso da entrambe le estremità della coda, a differenza delle altre code in cui è possibile farlo solo da un'estremità. A causa di questa proprietà, potrebbe non rispettare la proprietà First In First Out.

Applicazioni della coda:

La coda viene utilizzata quando le cose non devono essere elaborate immediatamente, ma devono essere elaborate F primo IO N F primo O ma ordina come Prima ricerca in ampiezza . Questa proprietà di Queue lo rende utile anche nei seguenti tipi di scenari.

• Quando una risorsa è condivisa tra più consumatori. Gli esempi includono la pianificazione della CPU e la pianificazione del disco.
Quando i dati vengono trasferiti in modo asincrono (i dati non sono necessariamente ricevuti alla stessa velocità di quelli inviati) tra due processi. Gli esempi includono buffer IO, pipe, file IO, ecc. La coda può essere utilizzata come componente essenziale in varie altre strutture dati.

Implementazione dell'array della coda:

Per implementare la coda, dobbiamo tenere traccia di due indici, anteriore e posteriore. Accodiamo un elemento nella parte posteriore e rimuoviamo dalla coda un elemento nella parte anteriore. Se incrementiamo semplicemente gli indici anteriore e posteriore, potrebbero verificarsi problemi, l'anteriore potrebbe raggiungere la fine dell'array. La soluzione a questo problema è aumentare l'anteriore e il posteriore in modo circolare.

Passaggi per l'accodamento:

1. Controlla che la coda sia piena o meno
2. Se è pieno, stampa in overflow ed esce
3. Se la coda non è piena, incrementa tail e aggiungi l'elemento

Passaggi per la rimozione dalla coda:

1. La coda di controllo è vuota o no
2. se vuoto, stampa underflow ed esce
3. se non è vuoto, stampa l'elemento in testa e incrementa testa

Di seguito è riportato un programma per implementare l'operazione sopra descritta sulla coda

C++

// CPP program for array> // implementation of queue> #include> using> namespace> std;> // A structure to represent a queue> class> Queue {> public> :> > int> front, rear, size;> > unsigned capacity;> > int> * array;> };> // function to create a queue> // of given capacity.> // It initializes size of queue as 0> Queue* createQueue(unsigned capacity)> {> > Queue* queue => new> Queue();> > queue->capacità = capacità;> > queue->fronte = coda->dimensione = 0;> > // This is important, see the enqueue> > queue->posteriore = capacità - 1;> > queue->matrice => new> int> [queue->capacità];> > return> queue;> }> // Queue is full when size> // becomes equal to the capacity> int> isFull(Queue* queue)> {> > return> (queue->dimensione == coda->capacità);> }> // Queue is empty when size is 0> int> isEmpty(Queue* queue)> {> > return> (queue->dimensione == 0);> }> // Function to add an item to the queue.> // It changes rear and size> void> enqueue(Queue* queue,> int> item)> {> > if> (isFull(queue))> > return> ;> > queue->posteriore = (coda->posteriore + 1)> > % queue->capacità;> > queue->array[coda->retro] = elemento;> > queue->dimensione = coda->dimensione + 1;> > cout < < item < <> ' enqueued to queue '> ;> }> // Function to remove an item from queue.> // It changes front and size> int> dequeue(Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > int> item = queue->array[coda->fronte];> > queue->fronte = (coda->fronte + 1)> > % queue->capacità;> > queue->dimensione = coda->dimensione - 1;> > return> item;> }> // Function to get front of queue> int> front(Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > return> queue->array[coda->fronte];> }> // Function to get rear of queue> int> rear(Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > return> queue->array[coda->posteriore];> }> // Driver code> int> main()> {> > Queue* queue = createQueue(1000);> > enqueue(queue, 10);> > enqueue(queue, 20);> > enqueue(queue, 30);> > enqueue(queue, 40);> > cout < < dequeue(queue)> > < <> ' dequeued from queue '> ;> > cout < <> 'Front item is '> > < < front(queue) < < endl;> > cout < <> 'Rear item is '> > < < rear(queue) < < endl;> > return> 0;> }> // This code is contributed by rathbhupendra>

C

// C program for array implementation of queue> #include> #include> #include> // A structure to represent a queue> struct> Queue {> > int> front, rear, size;> > unsigned capacity;> > int> * array;> };> // function to create a queue> // of given capacity.> // It initializes size of queue as 0> struct> Queue* createQueue(unsigned capacity)> {> > struct> Queue* queue = (> struct> Queue*)> malloc> (> > sizeof> (> struct> Queue));> > queue->capacità = capacità;> > queue->fronte = coda->dimensione = 0;> > // This is important, see the enqueue> > queue->posteriore = capacità - 1;> > queue->matrice = (> int> *)> malloc> (> > queue->capacità *> sizeof> (> int> ));> > return> queue;> }> // Queue is full when size becomes> // equal to the capacity> int> isFull(> struct> Queue* queue)> {> > return> (queue->dimensione == coda->capacità);> }> // Queue is empty when size is 0> int> isEmpty(> struct> Queue* queue)> {> > return> (queue->dimensione == 0);> }> // Function to add an item to the queue.> // It changes rear and size> void> enqueue(> struct> Queue* queue,> int> item)> {> > if> (isFull(queue))> > return> ;> > queue->posteriore = (coda->posteriore + 1)> > % queue->capacità;> > queue->array[coda->retro] = elemento;> > queue->dimensione = coda->dimensione + 1;> > printf> (> '%d enqueued to queue '> , item);> }> // Function to remove an item from queue.> // It changes front and size> int> dequeue(> struct> Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > int> item = queue->array[coda->fronte];> > queue->fronte = (coda->fronte + 1)> > % queue->capacità;> > queue->dimensione = coda->dimensione - 1;> > return> item;> }> // Function to get front of queue> int> front(> struct> Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > return> queue->array[coda->fronte];> }> // Function to get rear of queue> int> rear(> struct> Queue* queue)> {> > if> (isEmpty(queue))> > return> INT_MIN;> > return> queue->array[coda->posteriore];> }> // Driver program to test above functions./> int> main()> {> > struct> Queue* queue = createQueue(1000);> > enqueue(queue, 10);> > enqueue(queue, 20);> > enqueue(queue, 30);> > enqueue(queue, 40);> > printf> (> '%d dequeued from queue '> ,> > dequeue(queue));> > printf> (> 'Front item is %d '> , front(queue));> > printf> (> 'Rear item is %d '> , rear(queue));> > return> 0;> }>

Giava

// Java program for array> // implementation of queue> // A class to represent a queue> class> Queue {> > int> front, rear, size;> > int> capacity;> > int> array[];> > public> Queue(> int> capacity)> > {> > this> .capacity = capacity;> > front => this> .size => 0> ;> > rear = capacity -> 1> ;> > array => new> int> [> this> .capacity];> > }> > // Queue is full when size becomes> > // equal to the capacity> > boolean> isFull(Queue queue)> > {> > return> (queue.size == queue.capacity);> > }> > // Queue is empty when size is 0> > boolean> isEmpty(Queue queue)> > {> > return> (queue.size ==> 0> );> > }> > // Method to add an item to the queue.> > // It changes rear and size> > void> enqueue(> int> item)> > {> > if> (isFull(> this> ))> > return> ;> > this> .rear = (> this> .rear +> 1> )> > %> this> .capacity;> > this> .array[> this> .rear] = item;> > this> .size => this> .size +> 1> ;> > System.out.println(item> > +> ' enqueued to queue'> );> > }> > // Method to remove an item from queue.> > // It changes front and size> > int> dequeue()> > {> > if> (isEmpty(> this> ))> > return> Integer.MIN_VALUE;> > int> item => this> .array[> this> .front];> > this> .front = (> this> .front +> 1> )> > %> this> .capacity;> > this> .size => this> .size -> 1> ;> > return> item;> > }> > // Method to get front of queue> > int> front()> > {> > if> (isEmpty(> this> ))> > return> Integer.MIN_VALUE;> > return> this> .array[> this> .front];> > }> > // Method to get rear of queue> > int> rear()> > {> > if> (isEmpty(> this> ))> > return> Integer.MIN_VALUE;> > return> this> .array[> this> .rear];> > }> }> // Driver class> public> class> Test {> > public> static> void> main(String[] args)> > {> > Queue queue => new> Queue(> 1000> );> > queue.enqueue(> 10> );> > queue.enqueue(> 20> );> > queue.enqueue(> 30> );> > queue.enqueue(> 40> );> > System.out.println(queue.dequeue()> > +> ' dequeued from queue '> );> > System.out.println(> 'Front item is '> > + queue.front());> > System.out.println(> 'Rear item is '> > + queue.rear());> > }> }> // This code is contributed by Gaurav Miglani>

Python3

# Python3 program for array implementation of queue> # Class Queue to represent a queue> class> Queue:> > # __init__ function> > def> __init__(> self> , capacity):> > self> .front> => self> .size> => 0> > self> .rear> => capacity> -> 1> > self> .Q> => [> None> ]> *> capacity> > self> .capacity> => capacity> > > # Queue is full when size becomes> > # equal to the capacity> > def> isFull(> self> ):> > return> self> .size> => => self> .capacity> > > # Queue is empty when size is 0> > def> isEmpty(> self> ):> > return> self> .size> => => 0> > # Function to add an item to the queue.> > # It changes rear and size> > def> EnQueue(> self> , item):> > if> self> .isFull():> > print> (> 'Full'> )> > return> > self> .rear> => (> self> .rear> +> 1> )> %> (> self> .capacity)> > self> .Q[> self> .rear]> => item> > self> .size> => self> .size> +> 1> > print> (> '% s enqueued to queue'> %> str> (item))> > # Function to remove an item from queue.> > # It changes front and size> > def> DeQueue(> self> ):> > if> self> .isEmpty():> > print> (> 'Empty'> )> > return> > > print> (> '% s dequeued from queue'> %> str> (> self> .Q[> self> .front]))> > self> .front> => (> self> .front> +> 1> )> %> (> self> .capacity)> > self> .size> => self> .size> -> 1> > > # Function to get front of queue> > def> que_front(> self> ):> > if> self> .isEmpty():> > print> (> 'Queue is empty'> )> > print> (> 'Front item is'> ,> self> .Q[> self> .front])> > > # Function to get rear of queue> > def> que_rear(> self> ):> > if> self> .isEmpty():> > print> (> 'Queue is empty'> )> > print> (> 'Rear item is'> ,> self> .Q[> self> .rear])> # Driver Code> if> __name__> => => '__main__'> :> > queue> => Queue(> 30> )> > queue.EnQueue(> 10> )> > queue.EnQueue(> 20> )> > queue.EnQueue(> 30> )> > queue.EnQueue(> 40> )> > queue.DeQueue()> > queue.que_front()> > queue.que_rear()>

C#

// C# program for array implementation of queue> using> System;> namespace> GeeksForGeeks {> // A class to represent a linearqueue> class> Queue {> > private> int> [] ele;> > private> int> front;> > private> int> rear;> > private> int> max;> > public> Queue(> int> size)> > {> > ele => new> int> [size];> > front = 0;> > rear = -1;> > max = size;> > }> > // Function to add an item to the queue.> > // It changes rear and size> > public> void> enqueue(> int> item)> > {> > if> (rear == max - 1) {> > Console.WriteLine(> 'Queue Overflow'> );> > return> ;> > }> > else> {> > ele[++rear] = item;> > }> > }> > // Function to remove an item from queue.> > // It changes front and size> > public> int> dequeue()> > {> > if> (front == rear + 1) {> > Console.WriteLine(> 'Queue is Empty'> );> > return> -1;> > }> > else> {> > Console.WriteLine(ele[front] +> ' dequeued from queue'> );> > int> p = ele[front++];> > Console.WriteLine();> > Console.WriteLine(> 'Front item is {0}'> , ele[front]);> > Console.WriteLine(> 'Rear item is {0} '> , ele[rear]);> > return> p;> > }> > }> > // Function to print queue.> > public> void> printQueue()> > {> > if> (front == rear + 1) {> > Console.WriteLine(> 'Queue is Empty'> );> > return> ;> > }> > else> {> > for> (> int> i = front; i <= rear; i++) {> > Console.WriteLine(ele[i] +> ' enqueued to queue'> );> > }> > }> > }> }> // Driver code> class> Program {> > static> void> Main()> > {> > Queue Q => new> Queue(5);> > Q.enqueue(10);> > Q.enqueue(20);> > Q.enqueue(30);> > Q.enqueue(40);> > Q.printQueue();> > Q.dequeue();> > }> }> }>

Javascript

> // Queue class> class Queue> {> > // Array is used to implement a Queue> > constructor()> > {> > this> .items = [];> > }> > isEmpty()> > {> > // return true if the queue is empty.> > return> this> .items.length == 0;> > }> > enqueue(element)> > {> > // adding element to the queue> > this> .items.push(element);> > document.write(element +> ' enqueued to queue '> );> > }> > dequeue()> > {> > // removing element from the queue> > // returns underflow when called> > // on empty queue> > if> (> this> .isEmpty())> > return> 'Underflow '> ;> > return> this> .items.shift();> > }> > front()> > {> > // returns the Front element of> > // the queue without removing it.> > if> (> this> .isEmpty())> > return> 'No elements in Queue '> ;> > return> this> .items[0];> > }> > rear()> > {> > // returns the Rear element of> > // the queue without removing it.> > if> (> this> .isEmpty())> > return> 'No elements in Queue '> ;> > return> this> .items[> this> .items.length-1];> > }> }> // creating object for queue class> var> queue => new> Queue();> // Adding elements to the queue> queue.enqueue(10);> queue.enqueue(20);> queue.enqueue(30);> queue.enqueue(40);> // queue contains [10, 20, 30, 40]> // removes 10> document.write(queue.dequeue() +> ' dequeued from queue '> );> // queue contains [20, 30, 40]> // Front is now 20> document.write(> 'Front item is '> + queue.front() +> ' '> );> // printing the rear element> // Rear is 40> document.write(> 'Rear item is '> + queue.rear() +> ' '> );> // This code is contributed by Susobhan Akhuli> >

Produzione

10 enqueued to queue 20 enqueued to queue 30 enqueued to queue 40 enqueued to queue 10 dequeued from queue Front item is 20 Rear item is 40 

Analisi della complessità:

Complessità temporale

Operazioni	Complessità
Accodamento(inserimento)	O(1)
Deque(cancellazione)	O(1)
Davanti (Vai davanti)	O(1)
Posteriore (Prenditi posteriore)	O(1)
È pieno (Verifica che la coda sia piena o meno)	O(1)
IsEmpty(La coda di controllo è vuota o meno)	O(1)

Spazio ausiliario:
O(N) dove N è la dimensione dell'array per la memorizzazione degli elementi.

Vantaggi dell'implementazione dell'array:

• Facile da implementare.
• Una grande quantità di dati può essere gestita in modo efficiente con facilità.
• Operazioni come l'inserimento e l'eliminazione possono essere eseguite con facilità poiché seguono la regola first in first out.

Svantaggi dell'implementazione dell'array:

• Struttura dati statica, dimensione fissa.
• Se la coda ha un gran numero di operazioni di accodamento e deaccodamento, ad un certo punto (in caso di incremento lineare degli indici anteriori e posteriori) potremmo non essere in grado di inserire elementi nella coda anche se la coda è vuota (questo problema viene evitato utilizzando la coda circolare).
• La dimensione massima di una coda deve essere definita in anticipo.