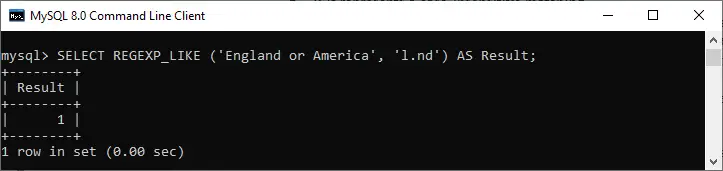
Minimális szegmensek a hétszegmenses kijelzőn
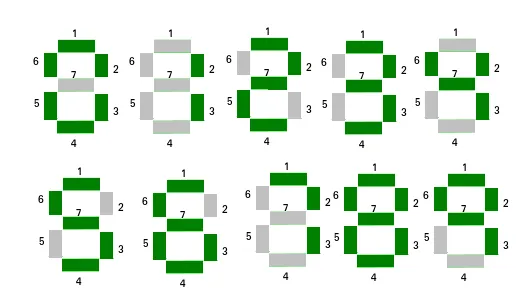
A számok megjelenítésére hétszegmenses kijelző használható. Adott egy tömb n természetes számok. A feladat az, hogy megkeressük a tömbben azt a számot, amely a minimális számú szegmenset használja a szám megjelenítéséhez. Ha több számnak van minimális számú szegmense, akkor a legkisebb indexű szám kerül kiadásra.

Példák:
Bemenet: arr[] = { 1 2 3 4 5 }.
Kimenet: 1
Magyarázat: A minimális számú szegmenset használó elem 1 (azaz 2 szegmens)Bemenet: arr[] = { 489 206 745 123 756 }.
Kimenet: 745
Magyarázat: A legkisebb indexű elem, amely a szegmensek minimális számát használja, 745 (azaz 12 szegmens)
Az ötlet az, hogy előre kiszámítsák a 0 és 9 közötti számjegyek által használt szegmensek számát, és eltárolják. Most a tömb minden eleméhez összegezze az egyes számjegyek által használt szegmensek számát. Ezután keresse meg azt az elemet, amely a minimális számú szegmenst használja.
C++A számjegyek által használt szegmens száma:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include using namespace std ; // Precomputed values of segment used by digit 0 to 9. const int seg [ 10 ] = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } int elementMinSegment ( vector < int > arr int n ) { // Initialising the minimum segment and minimum // number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } int main () { vector < int > arr = { 489 206 745 123 756 }; int n = arr . size (); cout < < elementMinSegment ( arr n ) < < endl ; return 0 ; }
Java import java.io.* ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = { 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ] ; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ] ; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ] ); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ] ); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ] ; } static public void main ( String [] args ) { int [] arr = { 489 206 745 123 756 }; int n = arr . length ; System . out . println ( elementMinSegment ( arr n )); } }
Python # Precomputed values of segment # used by digit 0 to 9. seg = [ 6 2 5 5 4 5 6 3 7 6 ] # Return the number of # segments used by x. def computeSegment ( x ): if ( x == 0 ): return seg [ 0 ] count = 0 # Finding sum of the segment # used by each digit of a number. while ( x ): count += seg [ x % 10 ] x = x // 10 return count # function to return minimum sum index def elementMinSegment ( arr n ): # Initialising the minimum # segment and minimum number index. minseg = computeSegment ( arr [ 0 ]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range ( 1 n ): temp = computeSegment ( arr [ i ]) # If arr[i] used less segment # then update minimum segment # and minimum number. if ( temp < minseg ): minseg = temp minindex = i return arr [ minindex ] # Driver Code arr = [ 489 206 745 123 756 ] n = len ( arr ) # function print required answer print ( elementMinSegment ( arr n )) # This code is contributed by # Sanjit_Prasad
C# using System ; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int [] seg = new int [ 10 ]{ 6 2 5 5 4 5 6 3 7 6 }; // Return the number of segments used by x. static int computeSegment ( int x ) { if ( x == 0 ) return seg [ 0 ]; int count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x /= 10 ; } return count ; } static int elementMinSegment ( int [] arr int n ) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment ( arr [ 0 ]); int minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( int i = 1 ; i < n ; i ++ ) { int temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } static public void Main () { int [] arr = { 489 206 745 123 756 }; int n = arr . Length ; Console . WriteLine ( elementMinSegment ( arr n )); } }
JavaScript // Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6 ]; // Return the number of segments used by x. function computeSegment ( x ) { if ( x == 0 ) return seg [ 0 ]; let count = 0 ; // Finding sum of the segment used by // each digit of a number. while ( x > 0 ) { count += seg [ x % 10 ]; x = parseInt ( x / 10 10 ); } return count ; } function elementMinSegment ( arr n ) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment ( arr [ 0 ]); let minindex = 0 ; // Finding and comparing segment used // by each number arr[i]. for ( let i = 1 ; i < n ; i ++ ) { let temp = computeSegment ( arr [ i ]); // If arr[i] used less segment then update // minimum segment and minimum number. if ( temp < minseg ) { minseg = temp ; minindex = i ; } } return arr [ minindex ]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr . length ; console . log ( elementMinSegment ( arr n ));
Kimenet
745
Időbonyolultság: O(n * log 10 n)
Segédtér: O(10)