Maximális elem a BST két csomópontja között
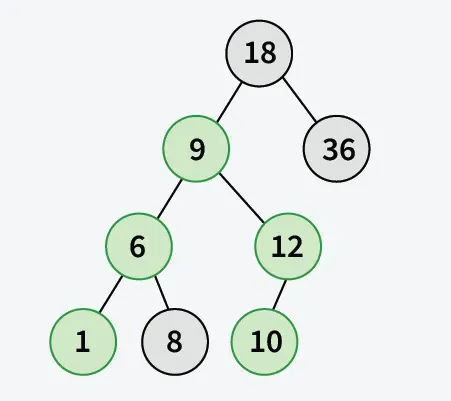
Adott egy tömb n elemek és két egész szám a b amelyek az adott tömbhöz tartoznak. Hozzon létre a Bináris keresőfa -ból elemek beszúrásával arr[0] – arr[n-1] . A feladat az, hogy megtaláljuk a maximális elem az a-tól b-ig tartó útvonalon.
Példa:
Bemenet: arr[] = { 18 36 9 6 12 10 1 8 } a = 1 b = 10.
Kimenet: 12
Magyarázat: Útvonal innen 1-től 10-ig tartalmaz { 1 6 9 12 10 } . A maximális elem 12.
Tartalomjegyzék
- [Naiv megközelítés] Hashing használata - O(n * log n) idő és O(n) tér
- [Várható megközelítés] Két csomópont – O(h) idő és O(h) tér – LCA használata
[Naiv megközelítés] Hashing használata - O(n * log n) idő és O(n) tér
Az ötlet az, hogy a hashmap tárolni a szülő az egyes csomópontok csomópontja a bináris keresőfa . Mindkét adott csomópontból kiindulhatunk, és felfelé haladhatunk az a-ban talált csomópontokat tároló fán készlet . Miután elértük a két csomópont gyökerét vagy közös ősét, végighaladhatunk a fán az egyes csomópontoktól, és megtalálhatjuk a maximális elemet találtunk a csomópontok halmazában.
Algoritmus lépései a fenti megközelítéshez:
- Hozzon létre egy üres hash tábla tárolni a szülő a bináris keresési fa minden csomópontjának csomópontja.
- Végezze el a mélységi keresés (DFS) a bináris keresési fa bejárását, és töltse fel a hash táblát az egyes csomópontok szülőcsomópontjával.
- Inicializálja a két mutatót p1 és p2 az adott csomópontokhoz.
- Inicializáljon két üres halmazt mondjuk s1 és s2 a fán való felhaladás során talált csomópontok tárolására p1 és p2 illetőleg.
- Míg p1 és p2 vannak nem egyenlő tegye a következőket:
- Ha p1 nem null add hozzá az s1 készlethez és frissítés p1 a szülőcsomópontjához a hash tábla segítségével.
- Ha p2 nem null add hozzá az s2 és frissítés p2 a szülőcsomópontjához a hash tábla segítségével.
- Keresse meg a metszéspont halmazát s1 és s2 azaz az s1-ben és s2-ben is közös csomópontok halmaza.
- Ebben a kereszteződésben találni maximális elemet, és küldje vissza.
Az alábbiakban bemutatjuk a fenti megközelítés megvalósítását:
C++ // C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int x ) { data = x ; left = right = nullptr ; } }; // Insert a new Node in Binary Search Tree void insertNode ( Node *& root int x ) { Node * current = root * parent = nullptr ; // Traverse to the correct position for insertion while ( current != nullptr ) { parent = current ; if ( x < current -> data ) current = current -> left ; else current = current -> right ; } // Insert new Node at the correct position if ( parent == nullptr ) root = new Node ( x ); else if ( x < parent -> data ) parent -> left = new Node ( x ); else parent -> right = new Node ( x ); } // DFS to populate parent map for each node void dfs ( Node * root unordered_map < Node * Node *> & parentMap Node * parent = nullptr ) { if ( ! root ) return ; // Store the parent of the current node if ( parent != nullptr ) { parentMap [ root ] = parent ; } // Recur for left and right children dfs ( root -> left parentMap root ); dfs ( root -> right parentMap root ); } // Function to find the node with the given value in the BST Node * findNode ( Node * root int val ) { if ( ! root ) return nullptr ; if ( root -> data == val ) return root ; Node * leftResult = findNode ( root -> left val ); if ( leftResult ) return leftResult ; return findNode ( root -> right val ); } // Find maximum element in the path between two nodes in BST int findMaxElement ( Node * root int x int y ) { unordered_map < Node * Node *> parentMap ; // Populate parent map with DFS dfs ( root parentMap ); // Find the nodes corresponding to the // values x and y Node * p1 = findNode ( root x ); Node * p2 = findNode ( root y ); // If nodes not found if ( ! p1 || ! p2 ) return -1 ; // Sets to store nodes encountered // while traversing up the tree unordered_set < Node *> s1 s2 ; // Variable to store the maximum // element in the path int maxElement = INT_MIN ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 ) { s1 . insert ( p1 ); maxElement = max ( maxElement p1 -> data ); // Move to parent node p1 = parentMap [ p1 ]; } if ( p2 ) { s2 . insert ( p2 ); maxElement = max ( maxElement p2 -> data ); p2 = parentMap [ p2 ]; } // Check if there's a common node // in both sets if ( s1 . count ( p2 )) break ; if ( s2 . count ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = max ( maxElement p1 -> data ); return maxElement ; } int main () { vector < int > arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . size (); Node * root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); cout < < findMaxElement ( root a b ) < < endl ; return 0 ; }
Java // Java program to find the maximum element in the path // between two Nodes of Binary Search Tree. import java.util.* ; class Node { int data ; Node left right ; Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node static void dfs ( Node root Map < Node Node > parentMap Node parent ) { if ( root == null ) return ; // Store the parent of the current node if ( parent != null ) { parentMap . put ( root parent ); } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST static Node findNode ( Node root int val ) { if ( root == null ) return null ; if ( root . data == val ) return root ; Node leftResult = findNode ( root . left val ); if ( leftResult != null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path between // two nodes in BST static int findMaxElement ( Node root int x int y ) { Map < Node Node > parentMap = new HashMap <> (); // Populate parent map with DFS dfs ( root parentMap null ); // Find the nodes corresponding to // the values x and y Node p1 = findNode ( root x ); Node p2 = findNode ( root y ); // If nodes not found if ( p1 == null || p2 == null ) return - 1 ; // Sets to store nodes encountered // while traversing up the tree Set < Node > s1 = new HashSet <> (); Set < Node > s2 = new HashSet <> (); // Variable to store the maximum element // in the path int maxElement = Integer . MIN_VALUE ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 != null ) { s1 . add ( p1 ); maxElement = Math . max ( maxElement p1 . data ); // Move to parent node p1 = parentMap . get ( p1 ); } if ( p2 != null ) { s2 . add ( p2 ); maxElement = Math . max ( maxElement p2 . data ); p2 = parentMap . get ( p2 ); } // Check if there's a common node in both sets if ( s1 . contains ( p2 )) break ; if ( s2 . contains ( p1 )) break ; } // Now both p1 and p2 point to their // Lowest Common Ancestor (LCA) maxElement = Math . max ( maxElement p1 . data ); return maxElement ; } public static void main ( String [] args ) { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . length ; Node root = new Node ( arr [ 0 ] ); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ] ); System . out . println ( findMaxElement ( root a b )); } }
Python # Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node : def __init__ ( self x ): self . data = x self . left = None self . right = None # Insert a new Node in Binary Search Tree def insert_node ( root x ): current = root parent = None # Traverse to the correct position for insertion while current is not None : parent = current if x < current . data : current = current . left else : current = current . right # Insert new Node at the correct position if parent is None : root = Node ( x ) elif x < parent . data : parent . left = Node ( x ) else : parent . right = Node ( x ) # DFS to populate parent map for each node def dfs ( root parent_map parent = None ): if root is None : return # Store the parent of the current node if parent is not None : parent_map [ root ] = parent # Recur for left and right children dfs ( root . left parent_map root ) dfs ( root . right parent_map root ) # Function to find the node with the given # value in the BST def find_node ( root val ): if root is None : return None if root . data == val : return root left_result = find_node ( root . left val ) if left_result : return left_result return find_node ( root . right val ) # Find maximum element in the path between # two nodes in BST def find_max_element ( root x y ): parent_map = {} # Populate parent map with DFS dfs ( root parent_map ) # Find the nodes corresponding to the # values x and y p1 = find_node ( root x ) p2 = find_node ( root y ) # If nodes not found if not p1 or not p2 : return - 1 # Sets to store nodes encountered # while traversing up the tree s1 = set () s2 = set () # Variable to store the maximum element in the path max_element = float ( '-inf' ) # Traverse up the tree from p1 and p2 # and add nodes to sets s1 and s2 while p1 != p2 : if p1 : s1 . add ( p1 ) max_element = max ( max_element p1 . data ) # Move to parent node p1 = parent_map . get ( p1 ) if p2 : s2 . add ( p2 ) max_element = max ( max_element p2 . data ) p2 = parent_map . get ( p2 ) # Check if there's a common node in both sets if p2 in s1 : break if p1 in s2 : break # Now both p1 and p2 point to their # Lowest Common Ancestor (LCA) max_element = max ( max_element p1 . data ) return max_element if __name__ == '__main__' : arr = [ 18 36 9 6 12 10 1 8 ] a b = 1 10 n = len ( arr ) root = Node ( arr [ 0 ]) for i in range ( 1 n ): insert_node ( root arr [ i ]) print ( find_max_element ( root a b ))
C# // C# program to find the maximum element in the path // between two Nodes of Binary Search Tree. using System ; using System.Collections.Generic ; class Node { public int data ; public Node left right ; public Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static public void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct // position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node static public void dfs ( Node root Dictionary < Node Node > parentMap Node parent ) { if ( root == null ) return ; // Store the parent of the current node if ( parent != null ) { parentMap [ root ] = parent ; } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST static public Node findNode ( Node root int val ) { if ( root == null ) return null ; if ( root . data == val ) return root ; Node leftResult = findNode ( root . left val ); if ( leftResult != null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path between // two nodes in BST static public int findMaxElement ( Node root int x int y ) { Dictionary < Node Node > parentMap = new Dictionary < Node Node > (); // Populate parent map with DFS dfs ( root parentMap null ); // Find the nodes corresponding to // the values x and y Node p1 = findNode ( root x ); Node p2 = findNode ( root y ); // If nodes not found if ( p1 == null || p2 == null ) return - 1 ; // Sets to store nodes encountered // while traversing up the tree HashSet < Node > s1 = new HashSet < Node > (); HashSet < Node > s2 = new HashSet < Node > (); // Variable to store the maximum element // in the path int maxElement = int . MinValue ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 != p2 ) { if ( p1 != null ) { s1 . Add ( p1 ); maxElement = Math . Max ( maxElement p1 . data ); // Move to parent node p1 = parentMap [ p1 ]; } if ( p2 != null ) { s2 . Add ( p2 ); maxElement = Math . Max ( maxElement p2 . data ); p2 = parentMap [ p2 ]; } // Check if there's a common node in both sets if ( s1 . Contains ( p2 )) break ; if ( s2 . Contains ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math . Max ( maxElement p1 . data ); return maxElement ; } static void Main () { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = arr . Length ; Node root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); Console . WriteLine ( findMaxElement ( root a b )); } }
JavaScript // JavaScript program to find the maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor ( x ) { this . data = x ; this . left = this . right = null ; } } // Insert a new Node in Binary Search Tree function insertNode ( root x ) { let current = root parent = null ; // Traverse to the correct position for insertion while ( current !== null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent === null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // DFS to populate parent map for each node function dfs ( root parentMap parent = null ) { if ( root === null ) return ; // Store the parent of the current node if ( parent !== null ) { parentMap . set ( root parent ); } // Recur for left and right children dfs ( root . left parentMap root ); dfs ( root . right parentMap root ); } // Function to find the node with the given // value in the BST function findNode ( root val ) { if ( root === null ) return null ; if ( root . data === val ) return root ; let leftResult = findNode ( root . left val ); if ( leftResult !== null ) return leftResult ; return findNode ( root . right val ); } // Find maximum element in the path // between two nodes in BST function findMaxElement ( root x y ) { let parentMap = new Map (); // Populate parent map with DFS dfs ( root parentMap ); // Find the nodes corresponding to the // values x and y let p1 = findNode ( root x ); let p2 = findNode ( root y ); // If nodes not found if ( p1 === null || p2 === null ) return - 1 ; // Sets to store nodes encountered let s1 = new Set (); let s2 = new Set (); // Variable to store the maximum // element in the path let maxElement = - Infinity ; // Traverse up the tree from p1 and p2 // and add nodes to sets s1 and s2 while ( p1 !== p2 ) { if ( p1 !== null ) { s1 . add ( p1 ); maxElement = Math . max ( maxElement p1 . data ); // Move to parent node p1 = parentMap . get ( p1 ); } if ( p2 !== null ) { s2 . add ( p2 ); maxElement = Math . max ( maxElement p2 . data ); p2 = parentMap . get ( p2 ); } // Check if there's a common node in both sets if ( s1 . has ( p2 )) break ; if ( s2 . has ( p1 )) break ; } // Now both p1 and p2 point to their Lowest // Common Ancestor (LCA) maxElement = Math . max ( maxElement p1 . data ); return maxElement ; } let arr = [ 18 36 9 6 12 10 1 8 ]; let a = 1 b = 10 ; let n = arr . length ; let root = new Node ( arr [ 0 ]); for ( let i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); console . log ( findMaxElement ( root a b ));
Kimenet
12
[Várható megközelítés] Két csomópont – O(h) idő és O(h) tér – LCA használata
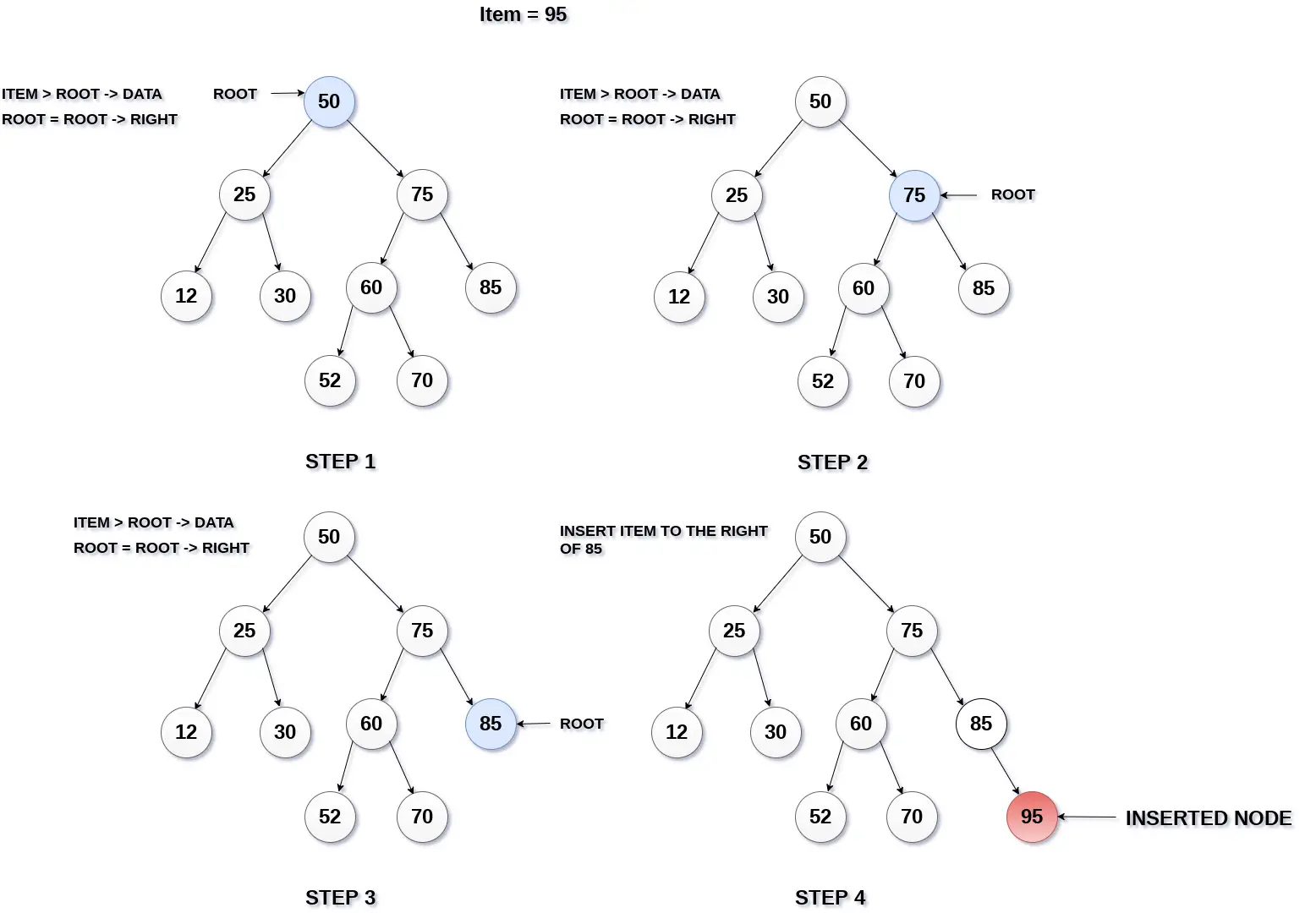
Az ötlet az, hogy megtaláljuk Legalacsonyabb közös őse az „a” és a „b” csomópontból. Ezután keresse meg a maximális csomópontot az LCA és az „a” között, valamint keresse meg a maximális csomópontot az LCA és „b” között. A válasz maximum kettős csomópont lesz.
Az alábbiakban bemutatjuk a fenti algoritmus megvalósítását:
C++ // C++ program to find maximum element in the path // between two Nodes of Binary Search Tree. #include using namespace std ; class Node { public : Node * left * right ; int data ; Node ( int x ) { data = x ; left = right = nullptr ; } }; // Insert a new Node in Binary Search Tree. void insertNode ( struct Node * root int x ) { Node * current = root * parent = nullptr ; while ( current != nullptr ) { parent = current ; if ( current -> data < x ) current = current -> right ; else current = current -> left ; } if ( parent == nullptr ) current = new Node ( x ); else { if ( parent -> data < x ) parent -> right = new Node ( x ); else parent -> left = new Node ( x ); } } // Return the maximum element between a Node // and its given ancestor. int maxelpath ( Node * root int x ) { Node * current = root ; int mx = INT_MIN ; // Traversing the path between ancestor and // Node and finding maximum element. while ( current -> data != x ) { if ( current -> data > x ) { mx = max ( mx current -> data ); current = current -> left ; } else { mx = max ( mx current -> data ); current = current -> right ; } } return max ( mx x ); } // Return maximum element in the path between // two given Node of BST. int maximumElement ( Node * root int x int y ) { Node * current = root ; // Finding the LCA of Node x and Node y while (( x < current -> data && y < current -> data ) || ( x > current -> data && y > current -> data )) { // Checking if both the Node lie on the // left side of the parent p. if ( x < current -> data && y < current -> data ) current = current -> left ; // Checking if both the Node lie on the // right side of the parent p. else if ( x > current -> data && y > current -> data ) current = current -> right ; } // Return the maximum of maximum elements occur // in path from ancestor to both Node. return max ( maxelpath ( current x ) maxelpath ( current y )); } int main () { int arr [] = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; int n = sizeof ( arr ) / sizeof ( arr [ 0 ]); Node * root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < n ; i ++ ) insertNode ( root arr [ i ]); cout < < maximumElement ( root a b ) < < endl ; return 0 ; }
Java // Java program to find maximum element in the path // between two Nodes of Binary Search Tree. import java.util.* ; class Node { int data ; Node left right ; Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct // position for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct // position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from // an ancestor to a node static int maxInPath ( Node root int x ) { int maxElement = Integer . MIN_VALUE ; Node current = root ; // Traverse the path from root to the // target node 'x' while ( current != null && current . data != x ) { maxElement = Math . max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . max ( maxElement x ); } // Find maximum element in the path between two // nodes in BST static int findMaxElement ( Node root int x int y ) { Node current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from LCA // to x and LCA to y return Math . max ( maxInPath ( current x ) maxInPath ( current y )); } public static void main ( String [] args ) { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; Node root = new Node ( arr [ 0 ] ); for ( int i = 1 ; i < arr . length ; i ++ ) insertNode ( root arr [ i ] ); System . out . println ( findMaxElement ( root a b )); } }
Python # Python program to find maximum element in the path # between two Nodes of Binary Search Tree. class Node : def __init__ ( self x ): self . data = x self . left = None self . right = None # Insert a new Node in Binary Search Tree def insertNode ( root x ): current = root parent = None # Traverse to the correct position for insertion while current is not None : parent = current if x < current . data : current = current . left else : current = current . right # Insert new Node at the correct position if parent is None : root = Node ( x ) elif x < parent . data : parent . left = Node ( x ) else : parent . right = Node ( x ) # Find maximum element in the path from an # ancestor to a node def maxInPath ( root x ): maxElement = float ( '-inf' ) current = root # Traverse the path from root to the # target node 'x' while current is not None and current . data != x : maxElement = max ( maxElement current . data ) if x < current . data : current = current . left else : current = current . right return max ( maxElement x ) # Find maximum element in the path between # two nodes in BST def findMaxElement ( root x y ): current = root # Find Lowest Common Ancestor (LCA) of x and y while ( x < current . data and y < current . data ) or ( x > current . data and y > current . data ): if x < current . data and y < current . data : current = current . left elif x > current . data and y > current . data : current = current . right # Find maximum elements in paths from LCA to # x and LCA to y return max ( maxInPath ( current x ) maxInPath ( current y )) if __name__ == '__main__' : arr = [ 18 36 9 6 12 10 1 8 ] a b = 1 10 root = Node ( arr [ 0 ]) for i in range ( 1 len ( arr )): insertNode ( root arr [ i ]) print ( findMaxElement ( root a b ))
C# // C# program to find maximum element in the path // between two Nodes of Binary Search Tree. using System ; class Node { public int data ; public Node left right ; public Node ( int x ) { data = x ; left = right = null ; } } class GfG { // Insert a new Node in Binary Search Tree static void insertNode ( Node root int x ) { Node current = root parent = null ; // Traverse to the correct position // for insertion while ( current != null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent == null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from an // ancestor to a node static int maxInPath ( Node root int x ) { int maxElement = int . MinValue ; Node current = root ; // Traverse the path from root to the target node 'x' while ( current != null && current . data != x ) { maxElement = Math . Max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . Max ( maxElement x ); } // Find maximum element in the path between two nodes in BST static int findMaxElement ( Node root int x int y ) { Node current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from // LCA to x and LCA to y return Math . Max ( maxInPath ( current x ) maxInPath ( current y )); } static void Main () { int [] arr = { 18 36 9 6 12 10 1 8 }; int a = 1 b = 10 ; Node root = new Node ( arr [ 0 ]); for ( int i = 1 ; i < arr . Length ; i ++ ) insertNode ( root arr [ i ]); Console . WriteLine ( findMaxElement ( root a b )); } }
JavaScript // JavaScript program to find maximum element in the path // between two Nodes of Binary Search Tree. class Node { constructor ( x ) { this . data = x ; this . left = null ; this . right = null ; } } // Insert a new Node in Binary Search Tree function insertNode ( root x ) { let current = root parent = null ; // Traverse to the correct position for insertion while ( current !== null ) { parent = current ; if ( x < current . data ) current = current . left ; else current = current . right ; } // Insert new Node at the correct position if ( parent === null ) root = new Node ( x ); else if ( x < parent . data ) parent . left = new Node ( x ); else parent . right = new Node ( x ); } // Find maximum element in the path from an // ancestor to a node function maxInPath ( root x ) { let maxElement = - Infinity ; let current = root ; // Traverse the path from root to the target node 'x' while ( current !== null && current . data !== x ) { maxElement = Math . max ( maxElement current . data ); if ( x < current . data ) current = current . left ; else current = current . right ; } return Math . max ( maxElement x ); } // Find maximum element in the path between // two nodes in BST function findMaxElement ( root x y ) { let current = root ; // Find Lowest Common Ancestor (LCA) of x and y while (( x < current . data && y < current . data ) || ( x > current . data && y > current . data )) { if ( x < current . data && y < current . data ) current = current . left ; else if ( x > current . data && y > current . data ) current = current . right ; } // Find maximum elements in paths from LCA to // x and LCA to y return Math . max ( maxInPath ( current x ) maxInPath ( current y )); } const arr = [ 18 36 9 6 12 10 1 8 ]; const a = 1 b = 10 ; const root = new Node ( arr [ 0 ]); for ( let i = 1 ; i < arr . length ; i ++ ) { insertNode ( root arr [ i ]); } console . log ( findMaxElement ( root a b ));
Kimenet
12Kvíz létrehozása