A leghosszabb egymást követő sorozat a bináris fában

 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; } Adott egy bináris fa, keresse meg a leghosszabb út hosszát, amely növekvő sorrendben egymást követő értékekkel rendelkező csomópontokat tartalmaz. Minden csomópontot 1 hosszúságú útvonalnak tekintünk.
Példák:
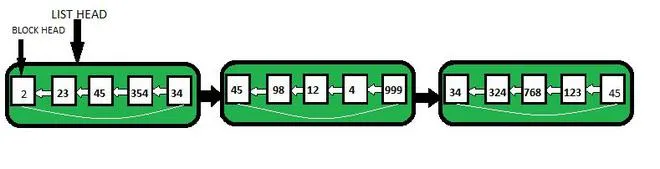
In below diagram binary tree with longest consecutive path(LCP) are shown :

A fenti problémát meg tudjuk oldani rekurzívan. Minden csomópontnál információra van szükségünk a szülőcsomópontjáról, ha az aktuális csomópont eggyel nagyobb értéket képvisel, mint a szülőcsomópontja, akkor minden csomóponton egy egymást követő útvonalat készít, összehasonlítjuk a csomópont értékét a szülőértékével, és ennek megfelelően frissítjük a leghosszabb egymást követő utat.
A szülőcsomópont értékének megszerzéséhez a (csomópont_értéke + 1) adjuk át argumentumként a rekurzív metódushoz, és összehasonlítjuk a csomópont értékét ezzel az argumentumértékkel, ha ez kielégíti, frissítse az egymást követő útvonal aktuális hosszát, ellenkező esetben újrainicializálja az aktuális útvonal hosszát 1-gyel.
Kérjük, olvassa el az alábbi kódot a jobb megértés érdekében:
C++ // C/C++ program to find longest consecutive // sequence in binary tree #include using namespace std ; /* A binary tree node has data pointer to left child and a pointer to right child */ struct Node { int data ; Node * left * right ; }; // A utility function to create a node Node * newNode ( int data ) { Node * temp = new Node ; temp -> data = data ; temp -> left = temp -> right = NULL ; return temp ; } // Utility method to return length of longest // consecutive sequence of tree void longestConsecutiveUtil ( Node * root int curLength int expected int & res ) { if ( root == NULL ) return ; // if root data has one more than its parent // then increase current length if ( root -> data == expected ) curLength ++ ; else curLength = 1 ; // update the maximum by current length res = max ( res curLength ); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil ( root -> left curLength root -> data + 1 res ); longestConsecutiveUtil ( root -> right curLength root -> data + 1 res ); } // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive ( Node * root ) { if ( root == NULL ) return 0 ; int res = 0 ; // call utility method with current length 0 longestConsecutiveUtil ( root 0 root -> data res ); return res ; } // Driver code to test above methods int main () { Node * root = newNode ( 6 ); root -> right = newNode ( 9 ); root -> right -> left = newNode ( 7 ); root -> right -> right = newNode ( 10 ); root -> right -> right -> right = newNode ( 11 ); printf ( '%d n ' longestConsecutive ( root )); return 0 ; }
Java // Java program to find longest consecutive // sequence in binary tree class Node { int data ; Node left right ; Node ( int item ) { data = item ; left = right = null ; } } class Result { int res = 0 ; } class BinaryTree { Node root ; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive ( Node root ) { if ( root == null ) return 0 ; Result res = new Result (); // call utility method with current length 0 longestConsecutiveUtil ( root 0 root . data res ); return res . res ; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil ( Node root int curlength int expected Result res ) { if ( root == null ) return ; // if root data has one more than its parent // then increase current length if ( root . data == expected ) curlength ++ ; else curlength = 1 ; // update the maximum by current length res . res = Math . max ( res . res curlength ); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil ( root . left curlength root . data + 1 res ); longestConsecutiveUtil ( root . right curlength root . data + 1 res ); } // Driver code public static void main ( String args [] ) { BinaryTree tree = new BinaryTree (); tree . root = new Node ( 6 ); tree . root . right = new Node ( 9 ); tree . root . right . left = new Node ( 7 ); tree . root . right . right = new Node ( 10 ); tree . root . right . right . right = new Node ( 11 ); System . out . println ( tree . longestConsecutive ( tree . root )); } } // This code is contributed by shubham96301
Python3 # Python3 program to find longest consecutive # sequence in binary tree # A utility class to create a node class newNode : def __init__ ( self data ): self . data = data self . left = self . right = None # Utility method to return length of # longest consecutive sequence of tree def longestConsecutiveUtil ( root curLength expected res ): if ( root == None ): return # if root data has one more than its # parent then increase current length if ( root . data == expected ): curLength += 1 else : curLength = 1 # update the maximum by current length res [ 0 ] = max ( res [ 0 ] curLength ) # recursively call left and right subtree # with expected value 1 more than root data longestConsecutiveUtil ( root . left curLength root . data + 1 res ) longestConsecutiveUtil ( root . right curLength root . data + 1 res ) # method returns length of longest consecutive # sequence rooted at node root def longestConsecutive ( root ): if ( root == None ): return 0 res = [ 0 ] # call utility method with current length 0 longestConsecutiveUtil ( root 0 root . data res ) return res [ 0 ] # Driver Code if __name__ == '__main__' : root = newNode ( 6 ) root . right = newNode ( 9 ) root . right . left = newNode ( 7 ) root . right . right = newNode ( 10 ) root . right . right . right = newNode ( 11 ) print ( longestConsecutive ( root )) # This code is contributed by PranchalK
C# // C# program to find longest consecutive // sequence in binary tree using System ; class Node { public int data ; public Node left right ; public Node ( int item ) { data = item ; left = right = null ; } } class Result { public int res = 0 ; } class GFG { Node root ; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive ( Node root ) { if ( root == null ) return 0 ; Result res = new Result (); // call utility method with current length 0 longestConsecutiveUtil ( root 0 root . data res ); return res . res ; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil ( Node root int curlength int expected Result res ) { if ( root == null ) return ; // if root data has one more than its parent // then increase current length if ( root . data == expected ) curlength ++ ; else curlength = 1 ; // update the maximum by current length res . res = Math . Max ( res . res curlength ); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil ( root . left curlength root . data + 1 res ); longestConsecutiveUtil ( root . right curlength root . data + 1 res ); } // Driver code public static void Main ( String [] args ) { GFG tree = new GFG (); tree . root = new Node ( 6 ); tree . root . right = new Node ( 9 ); tree . root . right . left = new Node ( 7 ); tree . root . right . right = new Node ( 10 ); tree . root . right . right . right = new Node ( 11 ); Console . WriteLine ( tree . longestConsecutive ( tree . root )); } } // This code is contributed by 29AjayKumar
JavaScript < script > // JavaScript program to find longest consecutive // sequence in binary tree class Node { constructor ( item ) { this . data = item ; this . left = this . right = null ; } } let res = 0 ; let root ; function longestConsecutive ( root ) { if ( root == null ) return 0 ; res = [ 0 ]; // call utility method with current length 0 longestConsecutiveUtil ( root 0 root . data res ); return res [ 0 ]; } // Utility method to return length of longest // consecutive sequence of tree function longestConsecutiveUtil ( root curlength expected res ) { if ( root == null ) return ; // if root data has one more than its parent // then increase current length if ( root . data == expected ) curlength ++ ; else curlength = 1 ; // update the maximum by current length res [ 0 ] = Math . max ( res [ 0 ] curlength ); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil ( root . left curlength root . data + 1 res ); longestConsecutiveUtil ( root . right curlength root . data + 1 res ); } // Driver code root = new Node ( 6 ); root . right = new Node ( 9 ); root . right . left = new Node ( 7 ); root . right . right = new Node ( 10 ); root . right . right . right = new Node ( 11 ); document . write ( longestConsecutive ( root )); // This code is contributed by rag2127 < /script>
Kimenet
3
Időkomplexitás: O(N), ahol N az adott bináris fa csomópontjainak száma.
Segédtér: O(log(N))
Az alábbi linken is szó van róla:
Maximális egymást követő növekvő útvonalhossz a bináris fában
Kvíz létrehozása