Legnagyobb szám a BST-ben, amely kisebb, mint k, vagy egyenlő azzal

Adott a gyökér Bináris keresőfa és egy egész szám k . A feladat az, hogy megtaláljuk a legnagyobb szám a bináris keresőfában kevesebb mint vagy egyenlő k-ra, ha nem létezik ilyen elem, nyomd meg a -1-et.
Példák:
Bemenet:

Kimenet: 21
Magyarázat: A 19 és 25 a 21-hez legközelebb eső két szám, a 19 pedig a legnagyobb szám, amelynek értéke kisebb vagy egyenlő, mint 21.
Bemenet: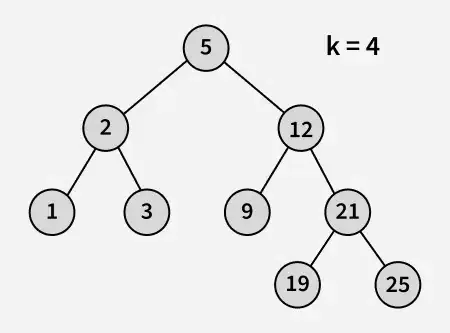
Kimenet: 3
Magyarázat: A 3 és 5 a 4-hez legközelebb eső két szám, a 3 pedig a legnagyobb szám, amelynek értéke kisebb vagy egyenlő 4-el.
Tartalomjegyzék
- [Naiv megközelítés] Rekurzió használata - O(h) idő és O(h) tér
- [Várható megközelítés] Iteráció használata - O(h) idő és O(1) tér
[Naiv megközelítés] Rekurzió használata - O(h) idő és O(h) tér
C++Az ötlet az, hogy a gyökér és hasonlítsa össze az értékét k-val. Ha a csomópont értéke nagyobb, mint k, lépjen a bal oldali részfára. Ellenkező esetben keresse meg a legnagyobb szám értékét, amely kisebb, mint k egyenlő jobb oldali részfa . Ha a jobb oldali részfa -1-et ad vissza (azaz nem létezik ilyen érték), akkor az aktuális csomópont értékét adja vissza. Ellenkező esetben a jobb oldali részfa által visszaadott értéket adja vissza (mivel nagyobb lesz, mint az aktuális csomópont értéke, de kisebb, mint k).
// C++ code to find the largest value // smaller than or equal to k using recursion #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int val ){ data = val ; left = nullptr ; right = nullptr ; } }; // function to find max value less than k int findMaxFork ( Node * root int k ) { // Base cases if ( root == nullptr ) return -1 ; if ( root -> data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root -> data < k ) { int x = findMaxFork ( root -> right k ); if ( x == -1 ) return root -> data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root -> left k ); } int main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node * root = new Node ( 5 ); root -> left = new Node ( 2 ); root -> left -> left = new Node ( 1 ); root -> left -> right = new Node ( 3 ); root -> right = new Node ( 12 ); root -> right -> left = new Node ( 9 ); root -> right -> right = new Node ( 21 ); root -> right -> right -> left = new Node ( 19 ); root -> right -> right -> right = new Node ( 25 ); cout < < findMaxFork ( root k ); return 0 ; }
Java // Java code to find the largest value // smaller than or equal to k using recursion class Node { int data ; Node left right ; Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int findMaxFork ( Node root int k ) { // Base cases if ( root == null ) return - 1 ; if ( root . data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { int x = findMaxFork ( root . right k ); if ( x == - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root . left k ); } public static void main ( String [] args ) { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); System . out . println ( findMaxFork ( root k )); } }
Python # Python code to find the largest value # smaller than or equal to k using recursion class Node : def __init__ ( self val ): self . data = val self . left = None self . right = None # function to find max value less than k def findMaxFork ( root k ): # Base cases if root is None : return - 1 if root . data == k : return k # If root's value is smaller # try in right subtree elif root . data < k : x = findMaxFork ( root . right k ) if x == - 1 : return root . data else : return x # If root's data is greater # return value from left subtree. return findMaxFork ( root . left k ) if __name__ == '__main__' : k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node ( 5 ) root . left = Node ( 2 ) root . left . left = Node ( 1 ) root . left . right = Node ( 3 ) root . right = Node ( 12 ) root . right . left = Node ( 9 ) root . right . right = Node ( 21 ) root . right . right . left = Node ( 19 ) root . right . right . right = Node ( 25 ) print ( findMaxFork ( root k ))
C# // C# code to find the largest value // smaller than or equal to k using recursion using System ; class Node { public int data ; public Node left right ; public Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int FindMaxFork ( Node root int k ) { // Base cases if ( root == null ) return - 1 ; if ( root . data == k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { int x = FindMaxFork ( root . right k ); if ( x == - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return FindMaxFork ( root . left k ); } static void Main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); Console . WriteLine ( FindMaxFork ( root k )); } }
JavaScript // JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor ( val ) { this . data = val ; this . left = null ; this . right = null ; } } // function to find max value less than k function findMaxFork ( root k ) { // Base cases if ( root === null ) return - 1 ; if ( root . data === k ) return k ; // If root's value is smaller // try in right subtree else if ( root . data < k ) { let x = findMaxFork ( root . right k ); if ( x === - 1 ) return root . data ; else return x ; } // If root's data is greater // return value from left subtree. return findMaxFork ( root . left k ); } let k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); console . log ( findMaxFork ( root k ));
Kimenet
21
[Várható megközelítés] Iteráció használata - O(h) idő és O(1) tér
C++Az ötlet az, hogy a gyökér és hasonlítsa össze az értékét azzal k . Ha a csomópont értéke <= k frissítse az eredmény értékét a root értékére, és lépjen a jobbra részfa másik mozgatni a balra részfa. Által iteratívan Ha ezt a műveletet az összes csomóponton alkalmazzuk, minimálisra csökkenthetjük a szükséges helyet rekurzió verem.
// C++ code to find the largest value // smaller than or equal to k using recursion #include using namespace std ; class Node { public : int data ; Node * left * right ; Node ( int val ){ data = val ; left = nullptr ; right = nullptr ; } }; // function to find max value less than k int findMaxFork ( Node * root int k ) { int result = -1 ; // Start from root and keep looking for larger while ( root != nullptr ) { // If root is smaller go to right side if ( root -> data <= k ){ result = root -> data ; root = root -> right ; } // If root is greater go to left side else root = root -> left ; } return result ; } int main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node * root = new Node ( 5 ); root -> left = new Node ( 2 ); root -> left -> left = new Node ( 1 ); root -> left -> right = new Node ( 3 ); root -> right = new Node ( 12 ); root -> right -> left = new Node ( 9 ); root -> right -> right = new Node ( 21 ); root -> right -> right -> left = new Node ( 19 ); root -> right -> right -> right = new Node ( 25 ); cout < < findMaxFork ( root k ); return 0 ; }
Java // Java code to find the largest value // smaller than or equal to k using recursion class Node { int data ; Node left right ; Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int findMaxFork ( Node root int k ) { int result = - 1 ; // Start from root and keep looking for larger while ( root != null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } public static void main ( String [] args ) { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); System . out . println ( findMaxFork ( root k )); } }
Python # Python code to find the largest value # smaller than or equal to k using recursion class Node : def __init__ ( self val ): self . data = val self . left = None self . right = None # function to find max value less than k def findMaxFork ( root k ): result = - 1 # Start from root and keep looking for larger while root is not None : # If root is smaller go to right side if root . data <= k : result = root . data root = root . right # If root is greater go to left side else : root = root . left return result if __name__ == '__main__' : k = 24 # creating following BST # # 5 # / # 2 12 # / / # 1 3 9 21 # / # 19 25 root = Node ( 5 ) root . left = Node ( 2 ) root . left . left = Node ( 1 ) root . left . right = Node ( 3 ) root . right = Node ( 12 ) root . right . left = Node ( 9 ) root . right . right = Node ( 21 ) root . right . right . left = Node ( 19 ) root . right . right . right = Node ( 25 ) print ( findMaxFork ( root k ))
C# // C# code to find the largest value // smaller than or equal to k using recursion using System ; class Node { public int data ; public Node left right ; public Node ( int val ) { data = val ; left = null ; right = null ; } } class GfG { // function to find max value less than k static int FindMaxFork ( Node root int k ) { int result = - 1 ; // Start from root and keep looking for larger while ( root != null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } static void Main () { int k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 Node root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); Console . WriteLine ( FindMaxFork ( root k )); } }
JavaScript // JavaScript code to find the largest value // smaller than or equal to k using recursion class Node { constructor ( val ) { this . data = val ; this . left = null ; this . right = null ; } } // function to find max value less than k function findMaxFork ( root k ) { let result = - 1 ; // Start from root and keep looking for larger while ( root !== null ) { // If root is smaller go to right side if ( root . data <= k ) { result = root . data ; root = root . right ; } // If root is greater go to left side else { root = root . left ; } } return result ; } let k = 24 ; // creating following BST // // 5 // / // 2 12 // / / // 1 3 9 21 // / // 19 25 let root = new Node ( 5 ); root . left = new Node ( 2 ); root . left . left = new Node ( 1 ); root . left . right = new Node ( 3 ); root . right = new Node ( 12 ); root . right . left = new Node ( 9 ); root . right . right = new Node ( 21 ); root . right . right . left = new Node ( 19 ); root . right . right . right = new Node ( 25 ); console . log ( findMaxFork ( root k ));
Kimenet
21Kvíz létrehozása