N-ágú fa átmérője
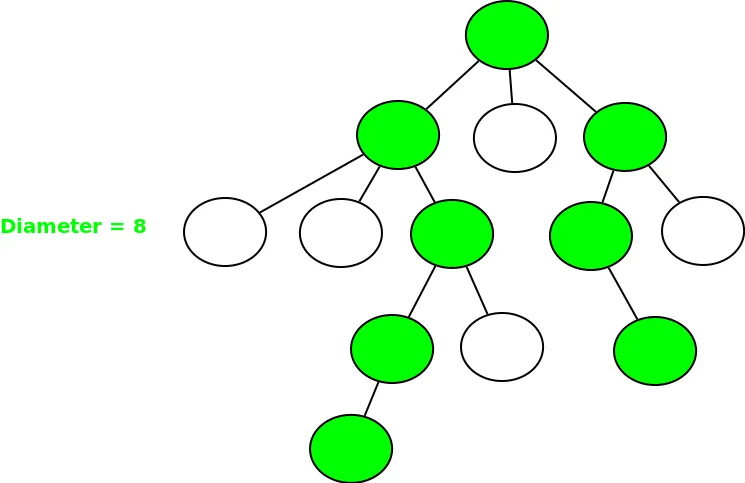
Egy N-ágú fa átmérője a fa bármely két csomópontja közötti leghosszabb út. Ennek a két csomópontnak két levélcsomópontnak kell lennie. A következő példákban a leghosszabb útvonal[átmérő] árnyékolva van.
1. példa:

2. példa:

Előfeltétel: Egy bináris fa átmérője .
Az útvonal kezdődhet az egyik csomóponttól, és felmehet ezen csomópontok egyik LCA-jáig, és ismét lejuthat egy másik részfa legmélyebb csomópontjához. vagy létezhet az aktuális csomópont egyik gyermekének átmérőjeként.
A megoldás a következők bármelyikében létezik:
- Az aktuális csomópont egyik gyermekének átmérője
- A legmagasabb két részfa magasságának összege + 1
Végrehajtás:
C++ // C++ program to find the height of an N-ary // tree #include using namespace std ; // Structure of a node of an n-ary tree struct Node { char key ; vector < Node *> child ; }; // Utility function to create a new tree node Node * newNode ( int key ) { Node * temp = new Node ; temp -> key = key ; return temp ; } // Utility function that will return the depth // of the tree int depthOfTree ( struct Node * ptr ) { // Base case if ( ! ptr ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) maxdepth = max ( maxdepth depthOfTree ( * it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree int diameter ( struct Node * ptr ) { // Base case if ( ! ptr ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) { int h = depthOfTree ( * it ); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) maxChildDia = max ( maxChildDia diameter ( * it )); return max ( maxChildDia max1 + max2 + 1 ); } // Driver program int main () { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node * root = newNode ( 'A' ); ( root -> child ). push_back ( newNode ( 'B' )); ( root -> child ). push_back ( newNode ( 'F' )); ( root -> child ). push_back ( newNode ( 'D' )); ( root -> child ). push_back ( newNode ( 'E' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'K' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'J' )); ( root -> child [ 2 ] -> child ). push_back ( newNode ( 'G' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'C' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'H' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'I' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'N' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'M' )); ( root -> child [ 3 ] -> child [ 2 ] -> child ). push_back ( newNode ( 'L' )); cout < < diameter ( root ) < < endl ; return 0 ; }
Java // Java program to find the height of an N-ary // tree import java.util.* ; class GFG { // Structure of a node of an n-ary tree static class Node { char key ; Vector < Node > child ; }; // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new Vector < Node > (); return temp ; } // Utility function that will return the depth // of the tree static int depthOfTree ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth for ( Node it : ptr . child ) maxdepth = Math . max ( maxdepth depthOfTree ( it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( Node it : ptr . child ) { int h = depthOfTree ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; for ( Node it : ptr . child ) maxChildDia = Math . max ( maxChildDia diameter ( it )); return Math . max ( maxChildDia max1 + max2 + 1 ); } // Driver Code public static void main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node root = newNode ( 'A' ); ( root . child ). add ( newNode ( 'B' )); ( root . child ). add ( newNode ( 'F' )); ( root . child ). add ( newNode ( 'D' )); ( root . child ). add ( newNode ( 'E' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'K' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'J' )); ( root . child . get ( 2 ). child ). add ( newNode ( 'G' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'C' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'H' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'I' )); ( root . child . get ( 0 ). child . get ( 0 ). child ). add ( newNode ( 'N' )); ( root . child . get ( 0 ). child . get ( 0 ). child ). add ( newNode ( 'M' )); ( root . child . get ( 3 ). child . get ( 2 ). child ). add ( newNode ( 'L' )); System . out . print ( diameter ( root ) + 'n' ); } } // This code is contributed by Rajput-Ji
Python3 # Python program to find the height of an N-ary # tree # Structure of a node of an n-ary tree class Node : def __init__ ( self x ): self . key = x self . child = [] # Utility function that will return the depth # of the tree def depthOfTree ( ptr ): # Base case if ( not ptr ): return 0 maxdepth = 0 # Check for all children and find # the maximum depth for it in ptr . child : maxdepth = max ( maxdepth depthOfTree ( it )) return maxdepth + 1 # Function to calculate the diameter # of the tree def diameter ( ptr ): # Base case if ( not ptr ): return 0 # Find top two highest children max1 max2 = 0 0 for it in ptr . child : h = depthOfTree ( it ) if ( h > max1 ): max2 max1 = max1 h elif ( h > max2 ): max2 = h # Iterate over each child for diameter maxChildDia = 0 for it in ptr . child : maxChildDia = max ( maxChildDia diameter ( it )) return max ( maxChildDia max1 + max2 + 1 ) # Driver program if __name__ == '__main__' : # /* Let us create below tree # * A # * / / # * B F D E # * / | /| # * K J G C H I # * / # * N M L # */ root = Node ( 'A' ) ( root . child ) . append ( Node ( 'B' )) ( root . child ) . append ( Node ( 'F' )) ( root . child ) . append ( Node ( 'D' )) ( root . child ) . append ( Node ( 'E' )) ( root . child [ 0 ] . child ) . append ( Node ( 'K' )) ( root . child [ 0 ] . child ) . append ( Node ( 'J' )) ( root . child [ 2 ] . child ) . append ( Node ( 'G' )) ( root . child [ 3 ] . child ) . append ( Node ( 'C' )) ( root . child [ 3 ] . child ) . append ( Node ( 'H' )) ( root . child [ 3 ] . child ) . append ( Node ( 'I' )) ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'N' )) ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'M' )) ( root . child [ 3 ] . child [ 2 ] . child ) . append ( Node ( 'L' )) print ( diameter ( root )) # This code is contributed by mohit kumar 29
C# // C# program to find the height of // an N-ary tree using System ; using System.Collections.Generic ; class GFG { // Structure of a node of an n-ary tree class Node { public char key ; public List < Node > child ; }; // Utility function to create // a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new List < Node > (); return temp ; } // Utility function that will return // the depth of the tree static int depthOfTree ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; int maxdepth = 0 ; // Check for all children and find // the maximum depth foreach ( Node it in ptr . child ) maxdepth = Math . Max ( maxdepth depthOfTree ( it )); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; foreach ( Node it in ptr . child ) { int h = depthOfTree ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter int maxChildDia = 0 ; foreach ( Node it in ptr . child ) maxChildDia = Math . Max ( maxChildDia diameter ( it )); return Math . Max ( maxChildDia max1 + max2 + 1 ); } // Driver Code public static void Main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ Node root = newNode ( 'A' ); ( root . child ). Add ( newNode ( 'B' )); ( root . child ). Add ( newNode ( 'F' )); ( root . child ). Add ( newNode ( 'D' )); ( root . child ). Add ( newNode ( 'E' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'K' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'J' )); ( root . child [ 2 ]. child ). Add ( newNode ( 'G' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'C' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'H' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). Add ( newNode ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). Add ( newNode ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). Add ( newNode ( 'L' )); Console . Write ( diameter ( root ) + 'n' ); } } // This code is contributed by Rajput-Ji
JavaScript < script > // Javascript program to find the // height of an N-ary tree // Structure of a node of an n-ary tree class Node { // Utility function to create a new tree node constructor ( key ) { this . key = key ; this . child = []; } } // Utility function that will // return the depth // of the tree function depthOfTree ( ptr ) { // Base case if ( ptr == null ) return 0 ; let maxdepth = 0 ; // Check for all children and find // the maximum depth for ( let it = 0 ; it < ptr . child . length ; it ++ ) maxdepth = Math . max ( maxdepth depthOfTree ( ptr . child [ it ])); return maxdepth + 1 ; } // Function to calculate the diameter // of the tree function diameter ( ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children let max1 = 0 max2 = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) { let h = depthOfTree ( ptr . child [ it ]); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } // Iterate over each child for diameter let maxChildDia = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) maxChildDia = Math . max ( maxChildDia diameter ( ptr . child [ it ])); return Math . max ( maxChildDia max1 + max2 + 1 ); } // Driver Code /* Let us create below tree * A * / / * B F D E * / | /| * K J G C H I * / * N M L */ let root = new Node ( 'A' ); ( root . child ). push ( new Node ( 'B' )); ( root . child ). push ( new Node ( 'F' )); ( root . child ). push ( new Node ( 'D' )); ( root . child ). push ( new Node ( 'E' )); ( root . child [ 0 ]. child ). push ( new Node ( 'K' )); ( root . child [ 0 ]. child ). push ( new Node ( 'J' )); ( root . child [ 2 ]. child ). push ( new Node ( 'G' )); ( root . child [ 3 ]. child ). push ( new Node ( 'C' )); ( root . child [ 3 ]. child ). push ( new Node ( 'H' )); ( root . child [ 3 ]. child ). push ( new Node ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). push ( new Node ( 'L' )); document . write ( diameter ( root ) + 'n' ); // This code is contributed by patel2127 < /script>
Kimenet
7
- Időbonyolultság: O(N)
- Térkomplexitás: O(N)
A fenti megoldás optimalizálása: Az átmérőt a fa mélységének kiszámítása nélkül is megtalálhatjuk, ha a fenti megoldásban kis változtatásokat hajtunk végre, hasonlóan a bináris fa átmérőjének megállapításához.
Végrehajtás:
C++ // C++ program to find the height of an N-ary // tree #include using namespace std ; // Structure of a node of an n-ary tree struct Node { char key ; vector < Node *> child ; }; // Utility function to create a new tree node Node * newNode ( int key ) { Node * temp = new Node ; temp -> key = key ; return temp ; } int diameter ( struct Node * ptr int & diameter_of_tree ) { // Base case if ( ! ptr ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( vector < Node *>:: iterator it = ptr -> child . begin (); it != ptr -> child . end (); it ++ ) { int h = diameter ( * it diameter_of_tree ); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Find whether our node can be part of diameter diameter_of_tree = max ( max1 + max2 + 1 diameter_of_tree ); return max ( max1 max2 ) + 1 ; } int main () { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node * root = newNode ( 'A' ); ( root -> child ). push_back ( newNode ( 'B' )); ( root -> child ). push_back ( newNode ( 'F' )); ( root -> child ). push_back ( newNode ( 'D' )); ( root -> child ). push_back ( newNode ( 'E' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'K' )); ( root -> child [ 0 ] -> child ). push_back ( newNode ( 'J' )); ( root -> child [ 2 ] -> child ). push_back ( newNode ( 'G' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'C' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'H' )); ( root -> child [ 3 ] -> child ). push_back ( newNode ( 'I' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'N' )); ( root -> child [ 0 ] -> child [ 0 ] -> child ). push_back ( newNode ( 'M' )); ( root -> child [ 3 ] -> child [ 2 ] -> child ). push_back ( newNode ( 'L' )); // for storing diameter int diameter_of_tree = 0 ; diameter ( root diameter_of_tree ); cout < < diameter_of_tree < < endl ; return 0 ; } // This code is improved by bhuvan
Java // Java program to find the height of an N-ary // tree import java.util.* ; class GFG { // Structure of a node of an n-ary tree static class Node { char key ; Vector < Node > child ; }; // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new Vector < Node > (); return temp ; } // for storing diameter_of_tree public static int diameter_of_tree = 0 ; // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; for ( Node it : ptr . child ) { int h = diameter ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } diameter_of_tree = Math . max ( max1 + max2 + 1 diameter_of_tree ); return ( Math . max ( max1 max2 ) + 1 ); } // Driver Code public static void main ( String [] args ) { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node root = newNode ( 'A' ); ( root . child ). add ( newNode ( 'B' )); ( root . child ). add ( newNode ( 'F' )); ( root . child ). add ( newNode ( 'D' )); ( root . child ). add ( newNode ( 'E' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'K' )); ( root . child . get ( 0 ). child ). add ( newNode ( 'J' )); ( root . child . get ( 2 ). child ). add ( newNode ( 'G' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'C' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'H' )); ( root . child . get ( 3 ). child ). add ( newNode ( 'I' )); ( root . child . get ( 0 ). child . get ( 0 ). child ) . add ( newNode ( 'N' )); ( root . child . get ( 0 ). child . get ( 0 ). child ) . add ( newNode ( 'M' )); ( root . child . get ( 3 ). child . get ( 2 ). child ) . add ( newNode ( 'L' )); diameter ( root ); System . out . print ( diameter_of_tree + 'n' ); } } // This code is improved by Bhuvan
Python3 # Python3 program to find the height of an N-ary # tree # Structure of a node of an n-ary tree # Structure of a node of an n-ary tree class Node : # Utility function to create a tree node def __init__ ( self key ): self . key = key ; self . child = []; diameter_of_tree = 0 ; def diameter ( ptr ): global diameter_of_tree # Base case # Base case if ( ptr == None ): return 0 ; # Find top two highest children max1 = 0 max2 = 0 ; for it in range ( len ( ptr . child )): h = diameter ( ptr . child [ it ]); if ( h > max1 ): max2 = max1 max1 = h ; elif ( h > max2 ): max2 = h ; # Find whether our node can be part of diameter diameter_of_tree = max ( max1 + max2 + 1 diameter_of_tree ); return max ( max1 max2 ) + 1 ; def main (): ''' us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L ''' root = Node ( 'A' ); ( root . child ) . append ( Node ( 'B' )); ( root . child ) . append ( Node ( 'F' )); ( root . child ) . append ( Node ( 'D' )); ( root . child ) . append ( Node ( 'E' )); ( root . child [ 0 ] . child ) . append ( Node ( 'K' )); ( root . child [ 0 ] . child ) . append ( Node ( 'J' )); ( root . child [ 2 ] . child ) . append ( Node ( 'G' )); ( root . child [ 3 ] . child ) . append ( Node ( 'C' )); ( root . child [ 3 ] . child ) . append ( Node ( 'H' )); ( root . child [ 3 ] . child ) . append ( Node ( 'I' )); ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'N' )); ( root . child [ 0 ] . child [ 0 ] . child ) . append ( Node ( 'M' )); ( root . child [ 3 ] . child [ 2 ] . child ) . append ( Node ( 'L' )); diameter ( root ); print ( diameter_of_tree ); main () # This code is contributed by phasing17.
C# // C# program to find the height of an N-ary // tree using System ; using System.Collections.Generic ; // Structure of a node of an n-ary tree class Node { public char key ; public List < Node > child ; }; class GFG { // Utility function to create a new tree node static Node newNode ( int key ) { Node temp = new Node (); temp . key = ( char ) key ; temp . child = new List < Node > (); return temp ; } // for storing diameter_of_tree public static int diameter_of_tree = 0 ; // Function to calculate the diameter // of the tree static int diameter ( Node ptr ) { // Base case if ( ptr == null ) return 0 ; // Find top two highest children int max1 = 0 max2 = 0 ; foreach ( Node it in ptr . child ) { int h = diameter ( it ); if ( h > max1 ) { max2 = max1 ; max1 = h ; } else if ( h > max2 ) max2 = h ; } diameter_of_tree = Math . Max ( max1 + max2 + 1 diameter_of_tree ); return ( Math . Max ( max1 max2 ) + 1 ); } // Driver Code public static void Main ( string [] args ) { /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ Node root = newNode ( 'A' ); ( root . child ). Add ( newNode ( 'B' )); ( root . child ). Add ( newNode ( 'F' )); ( root . child ). Add ( newNode ( 'D' )); ( root . child ). Add ( newNode ( 'E' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'K' )); ( root . child [ 0 ]. child ). Add ( newNode ( 'J' )); ( root . child [ 2 ]. child ). Add ( newNode ( 'G' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'C' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'H' )); ( root . child [ 3 ]. child ). Add ( newNode ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ) . Add ( newNode ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ) . Add ( newNode ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ) . Add ( newNode ( 'L' )); diameter ( root ); Console . Write ( diameter_of_tree + 'n' ); } } // This code is improved by phasing17
JavaScript // Javascript program to find the height of an N-ary // tree // Structure of a node of an n-ary tree // Structure of a node of an n-ary tree class Node { // Utility function to create a new tree node constructor ( key ) { this . key = key ; this . child = []; } } let diameter_of_tree = 0 ; function diameter ( ptr ) { // Base case // Base case if ( ptr == null ) return 0 ; // Find top two highest children let max1 = 0 max2 = 0 ; for ( let it = 0 ; it < ptr . child . length ; it ++ ) { let h = diameter ( ptr . child [ it ]); if ( h > max1 ) max2 = max1 max1 = h ; else if ( h > max2 ) max2 = h ; } // Find whether our node can be part of diameter diameter_of_tree = Math . max ( max1 + max2 + 1 diameter_of_tree ); return Math . max ( max1 max2 ) + 1 ; } /* Let us create below tree * A * / / * B F D E * / / /| * K J G C H I * / | * N M L */ let root = new Node ( 'A' ); ( root . child ). push ( new Node ( 'B' )); ( root . child ). push ( new Node ( 'F' )); ( root . child ). push ( new Node ( 'D' )); ( root . child ). push ( new Node ( 'E' )); ( root . child [ 0 ]. child ). push ( new Node ( 'K' )); ( root . child [ 0 ]. child ). push ( new Node ( 'J' )); ( root . child [ 2 ]. child ). push ( new Node ( 'G' )); ( root . child [ 3 ]. child ). push ( new Node ( 'C' )); ( root . child [ 3 ]. child ). push ( new Node ( 'H' )); ( root . child [ 3 ]. child ). push ( new Node ( 'I' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'N' )); ( root . child [ 0 ]. child [ 0 ]. child ). push ( new Node ( 'M' )); ( root . child [ 3 ]. child [ 2 ]. child ). push ( new Node ( 'L' )); diameter ( root diameter_of_tree ); console . log ( diameter_of_tree ); // This code is contributed by garg28harsh.
Kimenet
7
- Időbonyolultság: O(N^2)
- Segédtér: O(N+H) ahol N a fa csomópontjainak száma, H pedig a fa magassága.
Egy másik optimalizált megoldás: A leghosszabb út egy irányítatlan fában
Egy másik megközelítés az átmérő meghatározására DFS egy menetben:
A fa átmérője ugyanúgy kiszámítható, mint minden csomópont esetében
- Az aktuális csomópont nem része az átmérőnek (azaz az átmérő az aktuális csomópont egyik gyermekén fekszik).
- Az aktuális csomópont az átmérő része (azaz az átmérő áthalad az aktuális csomóponton).
Csomópont: Szomszédsági lista a fa tárolására szolgált.
Az alábbiakban bemutatjuk a fenti megközelítés megvalósítását:
C++ // C++ implementation to find // diameter of a tree using // DFS in ONE TRAVERSAL #include using namespace std ; #define maxN 10005 // The array to store the // height of the nodes int height [ maxN ]; // Adjacency List to store // the tree vector < int > tree [ maxN ]; // variable to store diameter // of the tree int diameter = 0 ; // Function to add edge between // node u to node v void addEdge ( int u int v ) { // add edge from u to v tree [ u ]. push_back ( v ); // add edge from v to u tree [ v ]. push_back ( u ); } void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node for ( auto u : tree [ cur ]) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = max ( height [ cur ] height [ u ]); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ]; } else if ( height [ u ] > max2 ) { max2 = height [ u ]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = max ( diameter height [ cur ]); diameter = max ( diameter max1 + max2 + 1 ); } // Driver Code int main () { // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); cout < < 'Diameter of tree is : ' < < diameter - 1 < < ' n ' ; return 0 ; }
Java /*package whatever //do not write package name here */ import java.io.* ; import java.util.* ; class GFG { static int maxN = 10005 ; // The array to store the // height of the nodes static int [] height = new int [ maxN ] ; // Adjacency List to store // the tree static ArrayList < ArrayList < Integer >> tree = new ArrayList < ArrayList < Integer >> (); // variable to store diameter // of the tree static int diameter = 0 ; // Function to add edge between // node u to node v static void addEdge ( int u int v ) { // add edge from u to v tree . get ( u ). add ( v ); // add edge from v to u tree . get ( v ). add ( u ); } static void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node for ( int u : tree . get ( cur )) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = Math . max ( height [ cur ] height [ u ] ); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ] ; } else if ( height [ u ] > max2 ) { max2 = height [ u ] ; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . max ( diameter height [ cur ] ); diameter = Math . max ( diameter max1 + max2 + 1 ); } public static void main ( String [] args ) { for ( int i = 0 ; i < maxN ; i ++ ) { tree . add ( new ArrayList < Integer > ()); } // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); System . out . println ( 'Diameter of tree is : ' + ( diameter - 1 )); } } // This code is contributed by ab2127.
Python3 # C++ implementation to find # diameter of a tree using # DFS in ONE TRAVERSAL maxN = 10005 # The array to store the # height of the nodes height = [ 0 for i in range ( maxN )] # Adjacency List to store # the tree tree = [[] for i in range ( maxN )] # variable to store diameter # of the tree diameter = 0 # Function to add edge between # node u to node v def addEdge ( u v ): # add edge from u to v tree [ u ] . append ( v ) # add edge from v to u tree [ v ] . append ( u ) def dfs ( cur par ): global diameter # Variables to store the height of children # of cur node with maximum heights max1 = 0 max2 = 0 # going in the adjacency list of the current node for u in tree [ cur ]: # if that node equals parent discard it if ( u == par ): continue # calling dfs for child node dfs ( u cur ) # calculating height of nodes height [ cur ] = max ( height [ cur ] height [ u ]) # getting the height of children # of cur node with maximum height if ( height [ u ] >= max1 ): max2 = max1 max1 = height [ u ] elif ( height [ u ] > max2 ): max2 = height [ u ] height [ cur ] += 1 # Diameter of a tree can be calculated as # diameter passing through the node # diameter doesn't includes the cur node diameter = max ( diameter height [ cur ]) diameter = max ( diameter max1 + max2 + 1 ) # Driver Code # n is the number of nodes in tree n = 7 # Adding edges to the tree addEdge ( 1 2 ) addEdge ( 1 3 ) addEdge ( 1 4 ) addEdge ( 2 5 ) addEdge ( 4 6 ) addEdge ( 4 7 ) # Calling the dfs function to # calculate the diameter of tree dfs ( 1 0 ) print ( 'Diameter of tree is :' diameter - 1 ) # This code is contributed by avanitrachhadiya2155
C# using System ; using System.Collections.Generic ; class GFG { static int maxN = 10005 ; // The array to store the // height of the nodes static int [] height = new int [ maxN ]; // Adjacency List to store // the tree static List < List < int >> tree = new List < List < int >> (); // variable to store diameter // of the tree static int diameter = 0 ; // Function to Add edge between // node u to node v static void AddEdge ( int u int v ) { // Add edge from u to v tree [ u ]. Add ( v ); // Add edge from v to u tree [ v ]. Add ( u ); } static void dfs ( int cur int par ) { // Variables to store the height of children // of cur node with maximum heights int max1 = 0 ; int max2 = 0 ; // going in the adjacency list of the current node foreach ( int u in tree [ cur ]) { // if that node equals parent discard it if ( u == par ) continue ; // calling dfs for child node dfs ( u cur ); // calculating height of nodes height [ cur ] = Math . Max ( height [ cur ] height [ u ]); // getting the height of children // of cur node with maximum height if ( height [ u ] >= max1 ) { max2 = max1 ; max1 = height [ u ]; } else if ( height [ u ] > max2 ) { max2 = height [ u ]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . Max ( diameter height [ cur ]); diameter = Math . Max ( diameter max1 + max2 + 1 ); } public static void Main ( string [] args ) { for ( int i = 0 ; i < maxN ; i ++ ) { tree . Add ( new List < int > ()); } // n is the number of nodes in tree int n = 7 ; // Adding edges to the tree AddEdge ( 1 2 ); AddEdge ( 1 3 ); AddEdge ( 1 4 ); AddEdge ( 2 5 ); AddEdge ( 4 6 ); AddEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); Console . WriteLine ( 'Diameter of tree is : ' + ( diameter - 1 )); } } // This code is contributed by phasing17.
JavaScript < script > // Javascript implementation to find // diameter of a tree using // DFS in ONE TRAVERSAL let maxN = 10005 ; // The array to store the // height of the nodes let height = new Array ( maxN ); // Adjacency List to store // the tree let tree = new Array ( maxN ); for ( let i = 0 ; i < maxN ; i ++ ) { height [ i ] = 0 ; tree [ i ] = []; } // variable to store diameter // of the tree let diameter = 0 ; // Function to add edge between // node u to node v function addEdge ( u v ) { // add edge from u to v tree [ u ]. push ( v ); // add edge from v to u tree [ v ]. push ( u ); } function dfs ( cur par ) { // Variables to store the height of children // of cur node with maximum heights let max1 = 0 ; let max2 = 0 ; // going in the adjacency list // of the current node for ( let u = 0 ; u < tree [ cur ]. length ; u ++ ) { // if that node equals parent discard it if ( tree [ cur ][ u ] == par ) continue ; // calling dfs for child node dfs ( tree [ cur ][ u ] cur ); // calculating height of nodes height [ cur ] = Math . max ( height [ cur ] height [ tree [ cur ][ u ]]); // getting the height of children // of cur node with maximum height if ( height [ tree [ cur ][ u ]] >= max1 ) { max2 = max1 ; max1 = height [ tree [ cur ][ u ]]; } else if ( height [ tree [ cur ][ u ]] > max2 ) { max2 = height [ tree [ cur ][ u ]]; } } height [ cur ] += 1 ; // Diameter of a tree can be calculated as // diameter passing through the node // diameter doesn't includes the cur node diameter = Math . max ( diameter height [ cur ]); diameter = Math . max ( diameter max1 + max2 + 1 ); } // Driver Code // n is the number of nodes in tree let n = 7 ; // Adding edges to the tree addEdge ( 1 2 ); addEdge ( 1 3 ); addEdge ( 1 4 ); addEdge ( 2 5 ); addEdge ( 4 6 ); addEdge ( 4 7 ); // Calling the dfs function to // calculate the diameter of tree dfs ( 1 0 ); document . write ( 'Diameter of tree is : ' + ( diameter - 1 )) // This code is contributed by unknown2108 < /script>
Kimenet
Diameter of tree is : 4
- Időbonyolultság: O(N) Ahol N az adott bináris fában lévő csomópontok száma.
- Segédtér: O(N)